Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Значима ли величина коэффициента ранговой корреляции Спирмена?

Для этого требуется проверить гипотезу: «коэффициент ранговой корреляции Спирмена равен 0». Альтернативная гипотеза будет такая: «коэффициент ранговой корреляции Спирмена отличен от 0». Принятие альтернативной гипотезы означает, что между исследуемыми признаками существует связь, а принятие основной гипотезы - что этой связи нет.

Проверка осуществляется следующим образом. Сначала мы выбираем уровень значимости гипотезы, например, α =0, 05. Затем вычисляем число степеней свободы для данного примера. Оно на 2 меньше, чем число наблюдений: d=N-2. В рассмотренном нами примере число степеней свободы d=8-2=6.

Далее, по таблице t-распределения Стьюдента с d=6 степенями свободы находим для наших данных критическое значение t_крит, соответствующее выбранному уровню значимости α. Обычно критическим значением (или критической точкой) называют граничное значение, с которым мы сравниваем коэффициент, чтобы определить, значим ли он. Пользователи Excel могут воспользоваться функцией СТЬЮДРАСПОБР. В нашем случае СТЬЮДРАСПОБР(0, 05; 6)= 2, 446914.

Далее по полученному нами значению ρ находим экспериментальное значение t_эксп по следующей формуле:

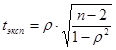
В нашем примере

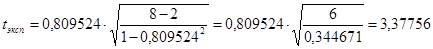
Сравниваем полученный в эксперименте коэффициент t_эксп (точнее, его модуль) с его критическим значением. Поскольку t_эксп=3, 37756 больше, чем критическое значение t_крит=2, 446914, мы отвергаем гипотезу о том, что коэффициент корреляции Спирмена равен 0 и утверждаем, что признаки связаны.

При использовании Excel возможно с помощью функции СТЬЮДРАСП найти по экспериментальному значению t_эксп уровень значимости α и сравнивать его с выбранным значением, например, 0.05. В нашем примере α _крит=0, 014903 < 0, 05.