Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Вопрос 8. Корреляция. Применения корреляции в измерении. Коэффициент ранговой корреляции Спирмена.

Коэффициенты корреляции используются для оценки силы связи между двумя признаками (в том числе при проверке того, есть ли эта связь вообще). Коэффициенты ранговой корреляции Спирмена и Кендалл а, о которых будет рассказано в этом разделе – это коэффициенты корреляции для проверки связи признаков, измеряемых по порядковым шкалам.

При вычислении коэффициентов ранговой корреляции каждому наблюдению (т.е. респонденту) ставится в соответствие величина, называемая рангом. Ранг имеет смысл порядкового номера ответа респондента после того, как ответы всех респондентов расположили в порядке возрастания исследуемого признака. Поясним на примере: Пусть были получены следующие ответы на некоторый вопрос:

Расположим ответы в порядке возрастания:

Теперь запишем вместо ответов порядковые номера ответов. Это и будут ранги:

Например, ранг 2-го респондента будет равен 4.

Процедуру присвоения рангов можно сделать и несколько иным образом. Сначала найдем среди ответов самый маленький (это ответ 2). Присвоим ему ранг 1. Теперь ищем самый маленький ответ среди оставшихся ответов (ответ 4). Присваиваем ему ранг 2. И так далее, до тех пор, пока все наблюдения не получат ранги.

Видно, что процедуру присвоения рангов можно выполнять для порядковых и интервальных шкал. Для номинальных шкал она неосуществима.

Как вычислить коэффициент ранговой корреляции Спирмена?.

Данные для его вычисления должны быть представлены в виде ответов респондентов на два вопроса. Скорее всего, это будут две строки или два столбца чисел, хотя вместо чисел могут быть и нечисловые ответы по порядковой шкале. Приведем пример данных:

Первым делом по каждому вопросу найдем ранги:

В результате мы имеем данные уже в виде рангов:

На следующем этапе мы вычисляем разности рангов:

Возводим их в квадрат и суммируем:

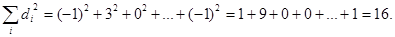
Формула для коэффициента корреляции Спирмена выглядит так: .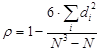

В ней кроме только что вычисленной суммы квадратов разностей рангов фигурирует еще число респондентов N, которое в нашем примере равно 8. Подставляем и вычисляем: .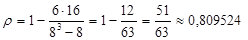

Коэффициент корреляции Спирмена может принимать значения от -1 до 1. Если коэффициент примерно равен 0, то связи нет. Если ρ ~1, то связь положительная: чем больше ранг 1-го ответа, тем больше ожидаемый ранг 2-го ответа. Если ρ ~-1, то связь есть, но отрицательная: чем больше ранг 1-го ответа, тем меньше ожидаемый ранг 2-го ответа. Тот же смысл имеет и коэффициент ранговой корреляции Кендалла, о вычислении которого будет рассказано далее на том же примере.