
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 2. Даны вершины треугольника ABC: A(– 2, 5), B(10, – 4), C(8, 10)
|
|
Даны вершины треугольника ABC: A (– 2, 5), B (10, – 4), C (8, 10). Требуется найти: 1) длину стороны AB; 2) уравнения сторон AB и AC в общем виде и их угловые коэффициенты; 3) угол A в радианах;
4) уравнение медианы AD; 5) уравнение высоты CE и ее длину;
6) уравнение окружности, для которой высота CE есть диаметр и точки пересечения этой окружности со стороной AC.
Решение.
1. Расстояние d между точками A (х 1; y 1) и B (х 2; y 2) вычисляем по формуле:
d = 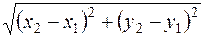 (1)
(1)
Применяя (1), находим длину стороны AB:
dAB = 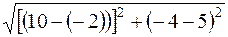 =
= 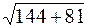 = 15.
= 15.
2. Уравнение прямой, проходящей через точки A (х 1; y 1) и B (х 2; y 2), имеет вид:
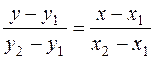 . (2)
. (2)
Подставив в (2) соответствующие координаты точек A и B находим уравнение прямой (AB):
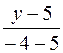 =
= 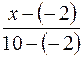 ;
; 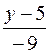 =
= 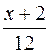 ;
;
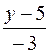 =
= 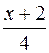 ; 4 y – 20 = – 3 x – 6; 3 x + 4 y – 14 = 0 (AB).
; 4 y – 20 = – 3 x – 6; 3 x + 4 y – 14 = 0 (AB).
Чтобы найти угловой коэффициент прямой AB (kAB), решим полученное уравнение прямой относительно y:
4 y = 3 x + 14, 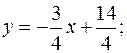 откуда
откуда 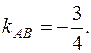
Подставляя в (2) координаты точек A и C, находим уравнения прямой (AC):
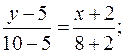
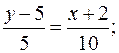
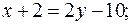
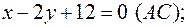 откуда
откуда 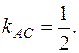
3. Если даны две прямые, угловые коэффициенты которых соответственно равны k 1 и k 2, то угол φ между этими прямыми определяется по формуле:
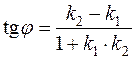 . (3)
. (3)
Искомый угол A образован прямыми AB и AC, угловые коэффициенты которых найдены ранее в пункте 2. Для определения угла A положим 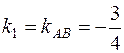 и
и 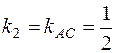 . Применяя (3), получим:
. Применяя (3), получим:
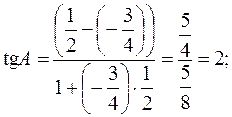 откуда
откуда 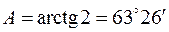 .
.
Используя таблицу перевода градусной меры в радианную, получим A = 1, 107 рад.
4. Если AD есть медиана, то точка D является серединой стороны BC. Для вычисления координат точки D применяем формулы деления отрезка на две равные части:
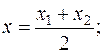
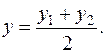 (4)
(4)
Подставив в (4) координаты точек B и C, находим координаты точки D:
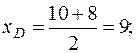
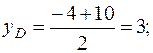 D (9; 3).
D (9; 3).
Подставив в (2) координаты точек A (– 2; 5) и D (9; 3), находим искомое уравнение медианы AD:
2 x + 11 y – 51 = 0 (AD).
5. Высота CE перпендикулярна стороне AB. Известно, что если две прямые взаимно перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку. Следовательно, 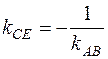 . Так как
. Так как 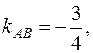 то
то 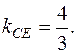
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Уравнение прямой, проходящей через данную точку, имеет вид:
 (5)
(5)
Подставив в (5) координаты точки C и найденный угловой коэффициент 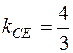 , получим искомое уравнение высоты CE:
, получим искомое уравнение высоты CE:
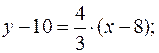
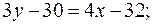
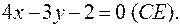
Чтобы найти длину CE, определим сперва координаты точки E – точки пересечения высоты CE и прямой AB. Для этого решаем совместно систему уравнений (AB) и (CE):
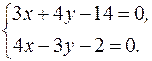
Решение этой системы дает x = 2 и y = 2. Следовательно, E (2; 2). Длину высоты CE определяем как расстояние между двумя точками по формуле (1).
dCE = 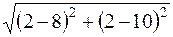 = 10.
= 10.
6. Ура
внение окружности с центром в точке K (a; b) и радиусом R имеет вид:
(x – a)2 + (y – b)2 = R 2. (6)
По условию, высота CE служит диаметром искомой окружности. Следовательно, центр окружности K является серединой отрезка CE. Используя (4), находим координаты точки K.
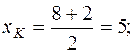
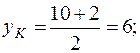 K (5; 6).
K (5; 6).
Так как dCE = 10, то радиус окружности R = 5. Следовательно,
(x – 5)2 + (y – 6)2 = 25 – уравнение искомой окружности. Чтобы найти точки пересечения этой окружности с прямой AC, решаем совместную систему уравнений:
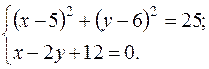
Решив эту систему, получим две точки пересечения C (8; 10) и М (0; 6). Треугольник ABC, медиана AD, высота CE, окружность с центром в точке K и точки ее пересечения со стороной AC построены в системе координат xOy на рис. 1.

Рисунок 1
|
|
