Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Й способ решения. Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:

Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:

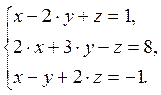
Решение. Обозначим через А – матрицу коэффициентов при неизвестных; Х – матрицу-столбец неизвестных x, y, z и Н – матрицу-столбец свободных членов:

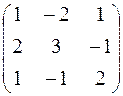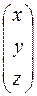А = , Х = , Н = .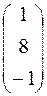

С учетом этих обозначений данная система уравнений принимает следующую матричную форму:

А · Х = Н. (1)

Если матрица А – невырожденная (ее определитель ∆ отличен от нуля), то она имеет обратную матрицу А ^–1. Умножив обе части уравнения (1) на А ^–1 слева, получим:

А ^–1 · А · Х = А ^–1 · Н.

Но А ^–1 · А = Е (Е – единичная матрица), а ЕХ = Х, поэтому

Х = А ^–1 · Н. (2)

Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А ^–1.

Пусть имеем невырожденную матрицу

А = . Тогда А ^–1 = ,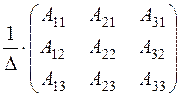

где А_ij (i = 1, 2, 3; j = 1, 2, 3) – алгебраическое дополнение элемента a_ij в определителе матрицы А, которое является произведением (– 1) ^{i + j} на минор (определитель) второго порядка, полученный вычеркиванием i -й строки j -го столбца в определителе матрицы А, т.е. A_ij = (– 1) ^{i + j} · M_ij.

Вычислим определитель ∆ и алгебраические дополнения А_ij элементов матрицы А.

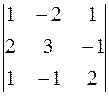∆ = = 10 ≠ 0, следовательно, матрица А имеет обратную матрицу А ^–1.

А ₁₁ = (– 1)¹⁺¹ ∙ 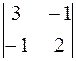= 5, А ₂₁ = (– 1)²⁺¹ ∙ 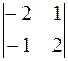= 3,

А ₁₂ = (– 1)¹⁺² ∙ 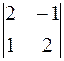= – 5, А ₂₂ = (– 1)²⁺² ∙ 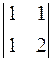= 1,

А ₁₃ = (– 1)¹⁺³ ∙ 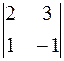= – 5, А ₂₃ = (– 1)²⁺³ ∙ 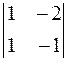= – 1,

А ₃₁ = (– 1)³⁺¹ ∙ 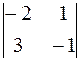= – 1, А ₃₂ = (– 1)³⁺² ∙ 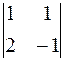= 3,

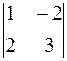А ₃₃ = (– 1)³⁺³ ∙ = 7.

Тогда А ^–1 = = .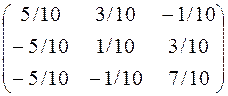

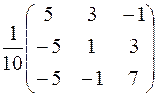По формуле (2) находим решение данной системы уравнений
в матричной форме:

Х = А ^–1 · Н = · · =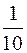
= · = · = .

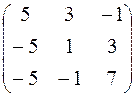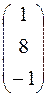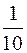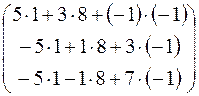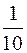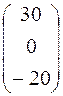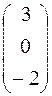Отсюда x = 3, y = 0, z = – 2.