II -й учебный вопрос. Понятие потока заявок- 35 мин

понятие потока заявок - 35 мин

Совокупность событий распределенных во времени называется потоком. Если событие заключается в появлении заявок, имеем поток заявок.

Для описания потока заявок, в общем случае, необходимо задать интервалы времени 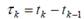между соседними моментами 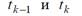поступления заявок с порядковыми номерами (k -1) и k соответственно (k = 1, 2,...; t ₀ = 0 – начальный момент времени).

Основной характеристикой потока заявок является его интенсивность  – среднее число заявок, проходящих через некоторую границу за единицу времени. Величина a = 1/l определяет средний интервал времени между двумя последовательными заявками.

Поток, в котором интервалы времени  _k между соседними заявками принимают определенные заранее известные значения, называется детерминированным. Если при этом интервалы одинаковы (t _k =t для всех k = 1, 2,...), то поток называется регулярным. Для полного описания регулярного потока заявок достаточно задать интенсивность потока l или значение интервала t = 1/l.

Поток, в котором интервалы  _k времени между соседними заявками представляют собой случайные величины, называется случайным. Для полного описания случайного потока заявок, в общем случае, необходимо задать законы распределений A_k (t _k) всех интервалов t _k (k = 1, 2,...).

Случайный поток, в котором все интервалы t1, t2, … между заявками независимы в совокупности и описываются функциями распределений A ₁(t₁), A ₂(t₂), …, называется потоком сограниченным последействием.

Случайный поток, в котором все интервалы t1, t2, … распределены по одному и тому же закону A (t), называется рекуррентным.

Поток заявок называется стационарным, если интенсивность l и закон распределения A (t) интервалов между последовательными заявками не меняются со временем. В противном случае поток заявок является нестационарным.

Поток заявок называется ординарным, если в каждый момент времени tk может появиться только одна заявка. Если в какой-либо момент времени может появиться более одной заявки, то имеем неординарный или групповой поток заявок.

Поток заявок называется потоком без последействия, если заявки поступают независимо друг от друга, то есть момент поступления очередной заявки не зависит от того, когда и сколько заявок поступило до этого момента.

Стационарный ординарный поток без последействия называется простейшим.

Интервалы времени  между заявками в простейшем потоке распределены по экспоненциальному закону с функцией распределения

A (t) = 1- e ^-lt, (3.1)

где l > 0 – параметр распределения, представляющий собой интенсивность потока заявок.

Простейший поток часто называют пуассоновским, поскольку число заявок k, поступающих за некоторый заданный промежуток времени t, распределено по закону Пуассона:

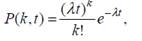, (3.2)

где P (k, t) – вероятность поступления ровно k заявок за некоторый фиксированный интервал времени t; l – интенсивность потока заявок. Здесь k – дискретная случайная величина, принимающая целочисленные значения: k = 0, 1, 2,..., а t > 0 и l> 0 – параметры закона Пуассона.

Следует отметить, что пуассоновский поток, в отличие от простейшего, может быть:

· стационарным, если интенсивность  не меняется со временем;

· нестационарным, если интенсивность потока зависит от времени: l = l(t).

В то же время, простейший поток, по определению, всегда является стационарным.

Аналитические исследования моделей массового обслуживания часто проводятся в предположении о простейшем потоке заявок, что обусловлено рядом присущих ему замечательных особенностей.

1. Суммирование (объединение) потоков. Сумма H независимых стационарных ординарных потоков с интенсивностями l₁, …, l _H образует простейший поток с интенсивностью

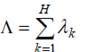, (3.3)

при условии, что складываемые потоки оказывают более или менее одинаково малое влияние на суммарный поток. На практике суммарный поток близок к простейшему при H  5. Очевидно, что при суммировании независимых простейших потоков суммарный поток будет простейшим при любом значении H.

2. Вероятностное разрежение потока. Вероятностное (но недетерминированное) разрежение простейшего потока заявок, при котором любая заявка случайным образом с некоторой вероятностью p исключается из потока независимо от того, исключены другие заявки или нет, приводит к образованию простейшего потока с интенсивностью l' = p l, где l – интенсивность исходного потока. Поток исключенных заявок – тоже простейший с интенсивностью l'' = (1 - p) l.

3. Простота. Предположение о простейшем потоке заявок позволяет для многих математических моделей сравнительно легко получить в явном виде зависимости характеристик от параметров. Наибольшее число аналитических результатов получено для простейшего потока заявок. Анализ моделей с потоками заявок, отличными от простейших, обычно усложняет математические выкладки и не всегда позволяет получить аналитическое решение в явном виде. Свое название «простейший» поток получил именно благодаря этой особенности

ВЫВОД