Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Адіабатний процес. Політропний процес
|
|
Адіабатний – це такий процес, який відбувається без обміну теплотою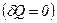 
між термодинамічною системою i оточуючим середовищем.
або 
.
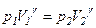Цей вираз називається рівнянням Пуассона.
.
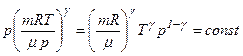Отже,
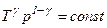і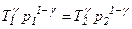 
.
Побудуємо графіки рівнянь:
1). 
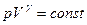(адіабата),
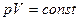(ізотерма)
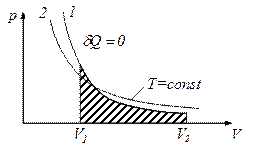
при адіабатному процесі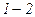 
. Вона вимірюється числово площею, заштрихованою на рисунку. Якщо газ адіабатно розширюється від об’єму 
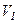до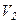 
, то його температура зменшується від 
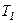до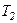 
і робота розширення ідеального газу
.
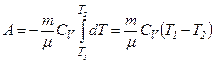В природі відбуваються реальні процеси, які є проміжними між адіабатними і ізотермічними. Такі процеси називаються політропними.
Політропним називається процес, при якому теплоємність тіла залишається сталою, тобто
,
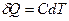де С=const.
Знайдемо рівняння політропи для ідеального газу. Запишемо рівняння першого закону термодинаміки:
.
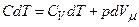Виключимо з цього рівняння Т. Для цього продиференціюємо вираз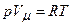 
:
.
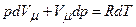Звідси
.
Підставимо dT у вираз для першого закону термодинаміки. Враховуючи, що,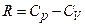 
, отримуємо
,
,
,
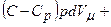
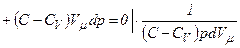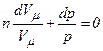де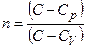 
- показник політропи.
Проінтегрувавши отриманий вираз, отримаємо:
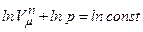і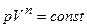 
.
Це рівняння і є шуканим рівнянням політропи ідеального газу.
При С=0,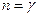 
із рівняння 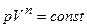отримуємо рівняння адіабати;
при С=∞, n=1 – рівняння ізотерми;
при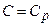 
, n=0 – рівняння ізобари;
при 
, 
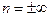– рівняння ізохори.
Отже, всі ізопроцеси в газах є частинними випадками політропного процесу.
|
|