Погрешности нейтронных данных и их ковариации

Погрешности используемых нейтронных данных являются одним из основных источников погрешностей результатов нейтронных расчётов (наряду с технологическими погрешностями, обуславливающими неточность использованных пр и расчётах ядерных концентраций и размеров, и методическими погрешностями расчёта (погрешностями многогруппового приближения и пр.). Оценка погрешностей нейтронных данных – дело весьма непростое. Оцененные кривые энергетических зависимостей нейтронных сечений опираются и на многочисленные, далеко не всегда хорошо согласующиеся между собой экспериментальные данные, и на результаты теоретических расчётов, позволяющих в общих чертах охарактеризовать энергетическое поведение сечений, и на данные различных систематик, позволяющих экстраполировать данные на те энергетические области или на те материалы, для которых экспериментальные данные отсутствуют. Однозначно оценить погрешности результатов всех этих процедур невозможно; субъективный фактор в этих оценках играет весьма большую роль. Однако каким бы экспертом не выполнялась оценка погрешностей нейтронных данных, её существенной особенностью является скоррелированность погрешностей сечений в разных энергетических областях и погрешностей сечений разных нуклидов. Для представления оцененных скоррелированных погрешностей оцененных нейтронных данных в библиотеках формата ENDF/B предусмотрены специальные средства. Для практического использования эти данные удобно представить в многогрупповой форме. В настоящее время в России принято 30-групповое представление данных о погрешностей. Первые 25 групп совпадают с первыми группами 26-групповой системы; 26-я группа БНАБ разделена на пять более узких групп. Оцененные данные о погрешностях хранятся в специальной библиотеке МАКОВКА (матрица ковариаций констант), состоящей из таблиц, по формату, близкому к формату таблиц БНАБ. Отличия со стоят в следующем.

В первой заголовочной строке после NAM= указываются наименования двух нуклидов, корреляции между погрешностями констант которых приводятся в этой таблице. Параметр МТ имеет форму MT=MT1*10+MT2, где МТ1- номер реакции первого материала, МТ2 – номер реакции второго материала. Используются следующие значения этих параметров:

1 – полное сечение;

2 – сечение поглощения без деления

3 – сечение деления;

4 – сечение упругого рассеяния;

5 – суммарное сечение неупругого рассеяния, реакции (n, 2n) и пр.;

6 – сечение реакции (n, 2n);

7 – число нейтронов, испускаемых при делении;

8 – средний косинус угла упругого рассеяния.

В таблицах для каждой группы g=1, 2, …, 30 приводится погрешность величины, определённой значением МТ1, и коэффициенты корреляции этой погрешности с погрешностями величины, определённой впараметром МТ2 во всех группах g’=1, 2, …, 30. Параметр BIB в таблицах Маковки используется для указания источника оценки ковариационных данных. Стандартный источник – ABBN – содержит данные, принятые разработчиками системы БНАБ. В библиотеке содержатся также данные, полученные на основе оценок ковариаций, принятых в библиотеках ENDF/B-V (BIB=B-5) и JENDL-3 (BIB=J-3) и др. Пример одного из фрагментов ковариационной матрицы, представленного в виде отдельной таблицы БНАБ, показан на рис.3.8.

Таким образом, система констант БНАБ содержит весь набор ядерных данных, необходимых для расчёта нейтронных полей и их функционалов, включая источники гамма-квантов; гамма-полей, порождённых этими источниками; функционалов гамма-полей, таких как энерговыделение и мощности дозы. Данные об образовании радионуклидов в результате нейтронных реакций и характеристики их распада достаточны для расчёта динамики нуклидного состава топлива в процессе облучения и последующей выдержки, а также для оценки радиационных характеристик отработавшего топлива и его фрагментов, образующихся в процессе химической переработки.

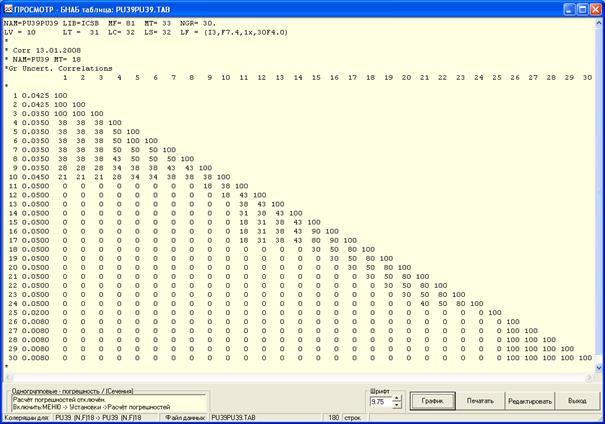
Рис.3.8. Пример таблицы погрешностей групповых сечений захвата U-235 и коэффициентов корреляции между ними из библиотеки Маковка.

[1] Причина, по которой величина, имеющая размерность обратной длины, получила название «сечение», будет разъяснено в разделе

[2] Поскольку мы рассматриваем здесь быстрые реакторы мы пренебрегаем возможностью приобретения энергии очень медленным нейтроном в результате столкновения с атомом среды, находящемся в тепловом движении.

[3] Ситенко А.Г. Теория ядерных реакций. Энергоиздат, 1983.

[4] Отсюда следует, что для выделения 1 ватта мощности в реакторе должно происходить 3.2*10¹⁰ делений в секунду.

[5] Энциклопедия нейтронных данных РОСФОНД. Обоснования отбора оцененных данных..

[6]Л.П.Абагян, Н.О.Базазянц, И.М.Бондаренко, М.Н.Николаев. Групповые константы для расчёта реакторов и защ иты. М.Атомиздат, 1964.

[7] Совокупность сферических функций образуют полную систему, т.е. в виде ряда по этим функциям можно разложить любое угловое распределение (правда, чем оно сложнее, тем большее число членов разложения потребуется для удовлетворительного описания заданного распределения). Сферические функции ортогональны:.

[8] Зачастую это приближение называют «приближением узкого резонанса» (имеется в виду узкого по сравнению с потерей энергии при рассеянии). На самом деле для оценки формы внутригруппового спектра важно лишь чтобы резонансы не проявлялись в энергетической зависимости плотности столкнрвений. Это усвловие выполняется и в том случае, если резонансы широки, но концентрация резонансного нуклида не слишком велика.

[9] Спектром нейтронов в такой среде является спектр Ферми, откуда и следует постоянство.

[10] Л.П.Абагян, Н.О. Базазянц, И.И. Бондаренко, М.Н.Николаев. Групповые константы для расчёта ядерных реакторов. М. Атомиздат, 1964.

Abagyan L.P., Bazazyants N.O. Bondarenko I.I. Nikolaev M.N. Group Constants for Nuclear reactor Calculations. N.Y. Consultants Bureau. 1964.

[11]М.Н.Никлоаев, Б.Г.Рязанов, М.М.Савоськин, А.М. Цибуля. Многогрупповое приближение в теории переноса нейтронов. М. Энергоатомиздат, 1984.

[12] Синица В.В., Николаев М.Н. Аналитический метод получения подгрупповых параметров.- Атомная Энергия, т.35, вып.6.с.429. 1973. С более поздним, совершенным, методом получения подгрупповых параметров можно познакомиться на сайте https://jini-zh.org/subgroups/subgroups.pdf

[13]Proc. of Int. Conf on Physics of Fast and Intermediate Reactors. IAEA. Vienna. 1962.

[14] Л.П.Абагян, Н.О.Базазянц, М.Н.Николаев, А.М.Цибуля. Групповые константы для расчёта реакторов и защиты. Энергоиздат, 1981.

[15] Мантуров Г.Н., Николаев М.Н., Цибуля А.М. Система групповых констант БНАБ-93. Часть 1 групповые константы для расчёта нейтронных и фотонных полей излучения. Вопросы атомной науки и техники, сер. Ядерные константы. 1996, вып.1. с. 59.

[16] V.V.Sinitsa, A.A.Rineiskiy. “GRUCON - A Package of Applied Computer Programs”, Rep. INDC(CCCP)-344, IAEA, Vienna, 1993.

[17] RSIC Peripheral Shielding Routine Collection. NJOY94, Code Sistem for Producing Pointwise and Multigroup Neutron and Photon Sections from ENDF/B Data, PSR-355. ORNL.

[18] За исключением последней, 26-й, группы, которая была разбита на 25 не равных по летаргии частей.

[19] Таблицы с MF=0 содержатся в заголовочном файле библиотеки БНАБ с именем NAM=HEAD.

[20] Власкин Г.Н., Жердев Г.М., Рогожкин В.Ю., Николаев М.Н. и др., Расчет интенсивности источников радиационных излучений (программа SOURCE).// Вопросы атомной науки и техники.Сер.Физика ядерных реакторов, 2002, вып.4.(стр.39-60)