
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многогрупповое приближение
|
|
Как видно из данных, приведенных в Приложении 1, энергетические зависимости нейтронных сечений весьма сложны и возможность их строгого учёта при решении уравнения переноса (3.1) весьма проблематична даже при использовании современных суперкомпьютеров. Естественными путём решения этой проблемы является разбиение энергетической оси на части, нейтроны, энергии которых лежат в пределах одной и той же части, объединить в соответствующую группу и приписать им некоторые эффективные среднегрупповые сечения. Проблема при этом сводится к тому, чтобы оценить энергетические спектры, по которым следует усреднять групповые сечения.
При разработке реакторов на тепловых нейтронах было принято трёхгрупповое приближени. Первую группу образовывали нейтроны, способные делить уран-238 (т.е. с энергиями выше эффективного порога деления, равного, примерно, 1.4 МэВ). Спектр нейтронов в этой энергетической области принимался совпадающим со спектром нейтронов деления. Вторую группу образовывали замедляющиеся нейтроны с энергиями выше, примерно, 0.5 эВ. Принималось, что спектр нейтронов в этой группе совпадает со спектром Ферми, Ф(Е)=Сonst/E, устанавливающемся в бесконечной замедляющей среде без поглощения с постоянным сечением рассеяния. Третью группу образовывали тепловые нейтроны, спектр которых принимался совпадающим со спектром Максвелла. Среднегрупповые сечения (групповые константы) могли быть измерены непосредственно с использованием нейтронов соответствующего спектра. Каждой группе соответствовал определённый сомножитель в формуле для коэффициента размножения: константы первой группы определяли коэффицент размножения на быстрых нейтронах; второй группы – вероятность избежать поглощения при замедлении; константы третьей, тепловой, группы определяли коэфициент использования тепловых нейтронов и среднее число нейтронов, образующихся при поглощении в топливе. Эти величины могли быть непосредственно измерены и в макроскопических экспериментах на критических и подкритических сборках, что при сопоставлении с результатами трёхгрупповых расчётов позволяло уточнить групповые константы.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
При разработке реакторов на быстрых нейтронах с самого начала было ясно, что оснований для качественной оценки формы спектра в них не имеется. При отсутствии замедлителя спектр нейтронов в области выше 1.4 МэВ может заметно отличаться от спектра деления, а поскольку роль делений урана-238 в быстром реакторе гораздо выше, чем в тепловом влияние неточности нейтронных данных для быстрых нейтронов будет намого существенней. Поглощение нейтронов в процессе замедления весьма велико и спектр нейтронов в области ниже 1.4 МэВ ничего общего со спектром Ферми не имеет. В этих условиях энергетическую ось требовалось разбивать на достаточно большое число групповых интервалов, а групповые константы требовалось получать путём усреднения оцененных данных. В пятидесятых годах погрешности этих данных были весьма велики и при использовании 10 - 20 энергетических групп неточности в оценке внутригрупповых спектрах влияли на результаты усреднения слабее, чем неточности усредняемых сеченний. Важно и то, что на первых этапах разработки и в СССР и в США рассматривались небольшие быстрые реакторы с низким содержанием урана-238 в топливе и с жестким энергетическим спектром, который не достигал резонансной области, представляющей особые сложности при усреднении.
В 60-х годах, когда в СССР началась разработка энергетических быстрых реакторов-размножителей (реакторов-бриддеров), потребности в усовершенствовании константного обеспечения резко возросли. Спектр нейтронов в этих реакторах несравненно мягче (в первую очередь за счет замедления нейтронов в результате неупругого рассеяния нейтронов на уране-238), рассматриваемый энергетический интервал расширился и для описания нейтронных спектров потребовалось вводить большее число энергетических групп. Существенно, что низкоэнергетические группы захватывали и область резонансных энергий, в которой оценка формы внутригруппового спектра требовала применения специальных приёмов и дополнительных приближений. Первой системой констант, обеспечивающей потребности расчёта энергетических быстрых реакторов, явилась 26-групповая система констант [2][6], разработанная в 1962 г. и появившаяся в печати (в СССР и в США) в 1964. За рубежом эта система констант по инициалам авторов получила наименование ABBN, а в СССР – БНАБ-64 (в отличие от более поздней, уточнённой версии БНАБ-70). В этой системе констант впервые был проведен учёт резонансной самоэкранировки сечений. Для пояснения явления резонансной самоэкранировки и методов его учёта нам потребуется представить уравнение переноса (3.5) в многогрупповой форме.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Чтобы получить многогрупповую форму уравнения переноса во можно было бы просто усреднить условно-критическое уравнение (3.5) (решение которого и является главной задачей проектных расчётов) по энергии каждой из групп. Среднегрупповые сечения, которые войдут в уравнение, будут зависеть от направления 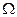 , от которого зависит плотность потока, с весом которого проводится усреднение. Например для среднегруппового полного сечения будем иметь:
, от которого зависит плотность потока, с весом которого проводится усреднение. Например для среднегруппового полного сечения будем иметь:
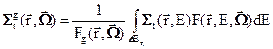 (3.32)
(3.32)
где групповая плотность потока
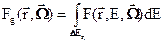 (3.33)
(3.33)
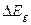 – энергетический интервал группы g.
– энергетический интервал группы g.
Координатная зависимость среднегруппового полного макроскопического сечения будет определяться не только пространственной зависимостью ядерных концентраций, отсутствующей в пределах гомогенных зон, но и координатной зависимостью плотности потока. Следовательно, от координат будут зависеть и среднегрупповые микроскопические сечения. Эти зависимости весьма неудобны и поскольку они, как правило, несущественны, встаёт задача о поиске приближённых выражений для плотности потока, которыми можно было бы заменить внутри-групповые потоки F(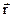 , E,
, E, 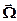 ), которые всё равно a-priori неизвестны. Задача состоит в том, чтобы выразить макроскопические среднегрупповые сечения через микроскопические групповые сечения нуклидов, входящих в состав среды, подобно тому, как это можно сделать при каждой конкретной энергии (см. (3.7)). Разумеется, требуется построить и алгоритмы вычисления среднегрупповых микроскопических сечений на основе оцененных нейтронных данных. Заметим, прежде всего, что в случае, когда сечения плавно зависят от энергии, как это имеет место, например, в случает сечений топливных материалов в области быстрых нейтронов (см. Приложение), то если группы не слишком широки, среднегрупповые сечения будут весьма слабо зависеть от того, с весом какой функции проводится усреднение по энергии. Проблема возникает усреднении сечений, обладающих резонансной структурой – в случае, если эта структура проявляется и в энергетической зависимости плотности потока нейтронов.
), которые всё равно a-priori неизвестны. Задача состоит в том, чтобы выразить макроскопические среднегрупповые сечения через микроскопические групповые сечения нуклидов, входящих в состав среды, подобно тому, как это можно сделать при каждой конкретной энергии (см. (3.7)). Разумеется, требуется построить и алгоритмы вычисления среднегрупповых микроскопических сечений на основе оцененных нейтронных данных. Заметим, прежде всего, что в случае, когда сечения плавно зависят от энергии, как это имеет место, например, в случает сечений топливных материалов в области быстрых нейтронов (см. Приложение), то если группы не слишком широки, среднегрупповые сечения будут весьма слабо зависеть от того, с весом какой функции проводится усреднение по энергии. Проблема возникает усреднении сечений, обладающих резонансной структурой – в случае, если эта структура проявляется и в энергетической зависимости плотности потока нейтронов.
При поиске пути решения проблемы обратим внимание на то, что индикатриса рассеяния (3.9) зависит только от косинуса угла рассеяния косинуса угла рассеяния 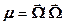 , Представим угловую зависимость этой индикатрисы в виде ряда по ортогональным полиномам Лежандра и ограничимся первыми двумя членами разложения (чём и будет состоять первое из потребующихся нам приближений):
, Представим угловую зависимость этой индикатрисы в виде ряда по ортогональным полиномам Лежандра и ограничимся первыми двумя членами разложения (чём и будет состоять первое из потребующихся нам приближений):
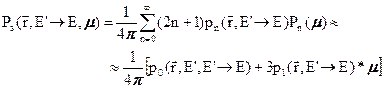 (3.34)
(3.34)
Проинтегрируем (3.34) по всем направлениям. Интеграл от первого члена разложения даст нами вероятность замедления из энергии E’ в энергию Е вне зависимости от изменения направления движения нейтрона в результате рассеяния:
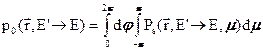 (3.35а)
(3.35а)
Интегралы от всех остальных членов будут равны нулю (все полиномы лежандра ортогональны нулевому полиному, равному единице).
Теперь умножим (3.34) на первый полином Лежандра, равный 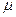 и снова проинтегрируем по всем направлениям. В силу ортогональности интегралы от всех членов разложения, кроме второго, обратятся в нуль, а интеграл от второго члена даст
и снова проинтегрируем по всем направлениям. В силу ортогональности интегралы от всех членов разложения, кроме второго, обратятся в нуль, а интеграл от второго члена даст
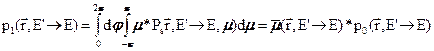 , (3.35б)
, (3.35б)
где 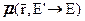 есть, очевидно, средний косинус угла рассеяния, сопровождающегося указанным изменением энергии.
есть, очевидно, средний косинус угла рассеяния, сопровождающегося указанным изменением энергии.
Далее, представим и угловую зависимость плотности потока нейтронов в виде ряда по сферическим функциям[7] Yn, m(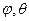 ) (здесь
) (здесь 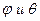 – углы, определяющие направление
– углы, определяющие направление 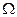 ) и также ограничимся первыми двумя членами разложения по n:
) и также ограничимся первыми двумя членами разложения по n:
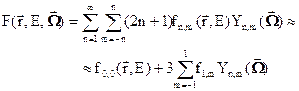 (3.36)
(3.36)
Первый член в этой формуле, очевидно, есть интеграл от плотности потока по всем направлениям, называемый глобальным потоком или, нередко, просто потоком (точнее – плотностью потока):
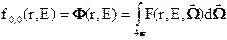 (3.37)
(3.37)
Второй член в разложении (3.36) можно представить в виде скалярного произведения двух векторов
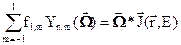
одним из которых является единичный вектор направления
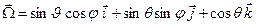 (3.38)
(3.38)
а второй вектор представим в виде
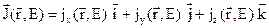 (3.38)
(3.38)
Умножив (3.35) на вектор 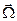 и проинтегрировав по всем его направлениям, найдём, что
и проинтегрировав по всем его направлениям, найдём, что
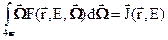 (3.39)
(3.39)
Эта величина имеет смысл тока нейтронов, т.е. разности между числом нейтронов, втекающих в единицу объема, и числом нейтронов той же энергии, вытекающих из него. Компоненнты вектора (3.38) суть координатные составляющие тока нейтронов, определяющие его направление. Таким образом, Р1- аппроксиманта плотности потока представима в виде
 . (3.40)
. (3.40)
Теперь нам следует записать всё уравнение переноса (3.5б) в Р1-приближении. Для этого представим в интеграле рассеяния 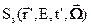 (первый интеграл в правой части этого уравнения, определённый формулой (3.2а)) индикатрису аппроксимантой (3.34), а плотность потока – аппроксимантой (3.40). Если полученное таким образом уравнение проинтегрировать по всем направлениям, то после преобразований, учитывающих свойства ортогональности сферических функций и их частного случая –полиномов Лежандра, получим следующее уравнение для потока нейтронов
(первый интеграл в правой части этого уравнения, определённый формулой (3.2а)) индикатрису аппроксимантой (3.34), а плотность потока – аппроксимантой (3.40). Если полученное таким образом уравнение проинтегрировать по всем направлениям, то после преобразований, учитывающих свойства ортогональности сферических функций и их частного случая –полиномов Лежандра, получим следующее уравнение для потока нейтронов
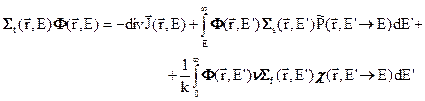 (3.41а)
(3.41а)
Если же перед интегрированием уравнение в Р1-приближении умножить на 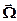 и после этого проинтегрировать по всем углам, получим уравнение для тока нейтронов:
и после этого проинтегрировать по всем углам, получим уравнение для тока нейтронов:
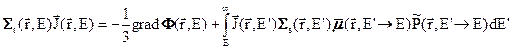 (3.41б)
(3.41б)
Последнее уравнение является, по существу, компактной записью трёх уравнений для трёх составляющих вектора тока 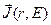 . Деление не даёт непосредственного вклада в ток нейтронов, поскольку нейтроны деления испускаются изотропно. Главным источником в уравнении (3.41б) является градиент нейтронного потока: ток нейтронов направлен противоположно градиенту, т.е. со стороны более высокой плотности потока в сторону меньшей его плотности. В представлении сферических тгармоник уравнение переноса можно было бы записать и в приближении, более высоком, чем Р1. Например в Р3-приближении к системе уравнений для потока и трёх составляющих тока добавились бы ещё 5 уравнений для составляющих второй гармоники потока и 7 уравнений для составляющих 3-й гармоники. Для решения проблемы угловой зависимости групповых констант естественно начать с Р1-приближения.
. Деление не даёт непосредственного вклада в ток нейтронов, поскольку нейтроны деления испускаются изотропно. Главным источником в уравнении (3.41б) является градиент нейтронного потока: ток нейтронов направлен противоположно градиенту, т.е. со стороны более высокой плотности потока в сторону меньшей его плотности. В представлении сферических тгармоник уравнение переноса можно было бы записать и в приближении, более высоком, чем Р1. Например в Р3-приближении к системе уравнений для потока и трёх составляющих тока добавились бы ещё 5 уравнений для составляющих второй гармоники потока и 7 уравнений для составляющих 3-й гармоники. Для решения проблемы угловой зависимости групповых констант естественно начать с Р1-приближения.
Перейдём в системе уравнений (3.41) к групповому приближению:
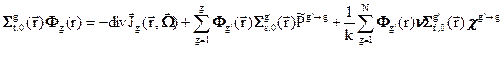 (3.42a)
(3.42a)
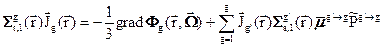 (3.42б)
(3.42б)
Нумерация групп начинается с самой высокоэнергетической группы. N- полное число групп. Средне-групповые параметры взаимодействия нейтронов со средой (групповые константы) в уравнении (3.42а) усреднены с весом потока 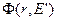 и поэтому их координатная зависимость обусловлена не толко координатной зависимостью ядерных концентраций, но и координатной зависимостью самого потока, если эта зависимость существенна. Групповые константы, фигурирующие в уравнении (3.42б), усреднены с весом тока нейтронов. Для вычисления групповых констант необходимо, очевидно, воспользоваться какими-то приближёнными оценками функций усреднения. При этом важно иметь в виду, что если число групп N достаточно велико, плавные изменения нейтронных сечений с приемлемой точностью могут быть описаны многогрупповыми гистограммами. Как уже отмечалось, главную проблему представляет учёт резонансной структуры сечений. Напомним, что для детального описания нейтронных сечений только одного изотопа требуется десятки тысяч энергетических точек – и это только в области разрешенных резонансов, а в области неразрешенных резонансов детальное описание стирукткры сечений в принципе невозможно. Поэтому оценка резонансной структуры функций усреднения является главнейшей задачей.
и поэтому их координатная зависимость обусловлена не толко координатной зависимостью ядерных концентраций, но и координатной зависимостью самого потока, если эта зависимость существенна. Групповые константы, фигурирующие в уравнении (3.42б), усреднены с весом тока нейтронов. Для вычисления групповых констант необходимо, очевидно, воспользоваться какими-то приближёнными оценками функций усреднения. При этом важно иметь в виду, что если число групп N достаточно велико, плавные изменения нейтронных сечений с приемлемой точностью могут быть описаны многогрупповыми гистограммами. Как уже отмечалось, главную проблему представляет учёт резонансной структуры сечений. Напомним, что для детального описания нейтронных сечений только одного изотопа требуется десятки тысяч энергетических точек – и это только в области разрешенных резонансов, а в области неразрешенных резонансов детальное описание стирукткры сечений в принципе невозможно. Поэтому оценка резонансной структуры функций усреднения является главнейшей задачей.
Для приближенной оценки 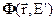 обратимся к уравнению (3.41а). Первое потребующееся нам приближение будет состоять в пренебрежении влияния тока на форму энергетической зависимости потока нейтронов. В этом случае при энергетическая зависимость плотности столкновений (величины, стоящей в левой части уравнения (3.41а)) будет опеределяться энергетической зависимостью источникам рассеянных нейтронов и источника нейтронов деления. Спектры нейтронов деления у всех делящихся ядер представляют собой плавные и близкие друг к другу функции энергии, т.е. форму энергетической зависимости последнего члена в уравнении (3.41а) можно считать известной. Для оценки энергетической зависимости интеграла рассеяния выделим в нём упругое рассеяние на отдельных нуклидах и неупругое рассеяние вкупе с реакциями (n, 2n), (n, 3n) и т.п.:
обратимся к уравнению (3.41а). Первое потребующееся нам приближение будет состоять в пренебрежении влияния тока на форму энергетической зависимости потока нейтронов. В этом случае при энергетическая зависимость плотности столкновений (величины, стоящей в левой части уравнения (3.41а)) будет опеределяться энергетической зависимостью источникам рассеянных нейтронов и источника нейтронов деления. Спектры нейтронов деления у всех делящихся ядер представляют собой плавные и близкие друг к другу функции энергии, т.е. форму энергетической зависимости последнего члена в уравнении (3.41а) можно считать известной. Для оценки энергетической зависимости интеграла рассеяния выделим в нём упругое рассеяние на отдельных нуклидах и неупругое рассеяние вкупе с реакциями (n, 2n), (n, 3n) и т.п.:
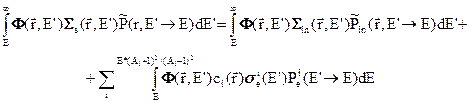
Потеря энергии при неупругом рассеянии велика, следовательно, интегрирование в первом интеграле ведётся по широкому энергетическому интервалу и никакой резонансной структуры в нём проявиться не может. В интегралах упругого рассеяния на отделных нуклидах интегрирование ведётся от рассматриваемой энергии Е, до максимальной энергии, с которой возможно замедление до энергии Е при упругом рассеянии на нуклиде i. Для водорода с А=1 эта энергия бесконечно велика; для урана или плутония она составляет 1.017*Е. В реакторах на быстрых нейтронах подавляющее большинство нейтронных реакций происходит при энергиях выше 1000 эВ. Таким образом, даже при этой энергии интегрирование по E’ в интегралах, учитывающих рассеяние даже на топливных нуклидах, проводится по интервалу 17 эВ, что намного не только ширины резонансов тяжелых ядер при этой энергии, но и расстояние между этими резонансами. Таким образом, резонансная структура сечений топливных материалов в энергетической зависимости плотности столкновений проявиться не может. У натрия имеется сильный резонанс при 2.78 кэВ, ширина которого составляет 0.37 кэВ. Потеря энергии при упругом рассеянии на топливных нуклидах при 3 кэВ составляет 0.5 кэВ, т.о. это резонанс нельзя считать безусловно узким по сравнению с потерей энергии при упругом рассеянии. Это приведёт к некоторой нерегулярности в энергетическом поведении плотности столкновений. Близкая ситуация имеет место и в окрестности низколежащих резонансов конструкционных материалов.
Чтобы построить алгоритм вычисления групповых констант этими нерегулярностями приходится пренебрегать, т.е. принимается приближение плавной энергетической зависимости плотности столкновений[8], т.е. принимается, что 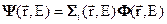 - плавная функция энергии. В этом случае для групповых констант, фигурирующих в уравнении (3.42а) для потока нейтронов получаем следующие формулы:
- плавная функция энергии. В этом случае для групповых констант, фигурирующих в уравнении (3.42а) для потока нейтронов получаем следующие формулы:
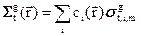 ; (3.43а)
; (3.43а) 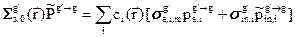 ; (3.43б)
; (3.43б)
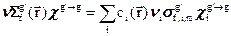 , (3.43в)
, (3.43в)
где групповые микроскопические константы для гомогенной среды определённого состава (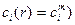 определены путём усреднения с весом
определены путём усреднения с весом 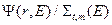 .
. 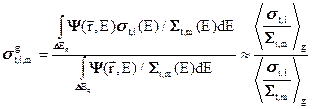 ; (3.44а)
; (3.44а)
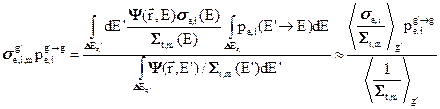 (3.44б)
(3.44б)
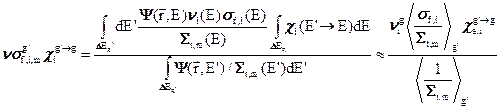 (3.44в)
(3.44в)
 Здесь везде угловые скобки означают усреднение по групповому интервалу с весом некоторого стандартного спектра
Здесь везде угловые скобки означают усреднение по групповому интервалу с весом некоторого стандартного спектра 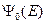 , которым при вычислении групповых констант мы заменяется a-priori неизвестная энергетическая зависимость плотности стокновений (с чем и связана приближенность последних равенств в формулах (3.44)).
, которым при вычислении групповых констант мы заменяется a-priori неизвестная энергетическая зависимость плотности стокновений (с чем и связана приближенность последних равенств в формулах (3.44)).
При вычислении групповых констант оказывается удобным рассматривать энергетические зависимости в логарифмическом масштабе, для чего энергия заменяется на летаргию 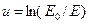 . В масштабе летаргии плотность столкновений в среде с постоянными сечениями при энергиях ниже энергии нейтронов источника при отсутсвии утечки и поглощения есть величина постоянная[9], так что отличие
. В масштабе летаргии плотность столкновений в среде с постоянными сечениями при энергиях ниже энергии нейтронов источника при отсутсвии утечки и поглощения есть величина постоянная[9], так что отличие 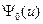 от константы учитывает отличие реального спектра от этого предельного случая.
от константы учитывает отличие реального спектра от этого предельного случая.
С учётом этого замечания можем записать
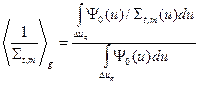 ;
; 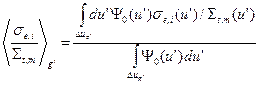 . (3.45а, б)
. (3.45а, б)
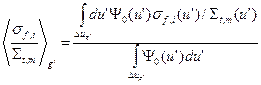 . (3.45в)
. (3.45в)
Здесь 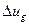 - интервал группы g в масштабе летаргии.
- интервал группы g в масштабе летаргии.
Величины, стоящие в формулах (3.44) вне угловых скобок, считаются не зависящими от энергии и они могут быть вынесены за знак усреднения при среднегрупповых значениях, оцененных без учёта влияния энергетической зависимости полного макроскопического сечения. В частности
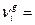
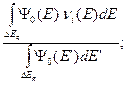
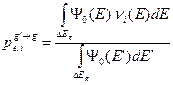 (3.46а, б)
(3.46а, б)
К этим величинам относятся также 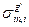 и
и 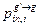 . Эти величины не зависят от состава среды m и могут для всех нужных нуклидов быть рассчитаны заранее, по крайней мере, в первом приближении, предполагающем, что отличия реальной энергетической зависимости плотности столкновений от стандартногот спектра не существенно влияет на эти величины. На величинах
. Эти величины не зависят от состава среды m и могут для всех нужных нуклидов быть рассчитаны заранее, по крайней мере, в первом приближении, предполагающем, что отличия реальной энергетической зависимости плотности столкновений от стандартногот спектра не существенно влияет на эти величины. На величинах 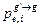 в случае, если группы достатрочно широки, эти отличия сказываются существенно, поэтому пв процессе подготовки констант к расчту в них приходится вводить специальные поправки (см.3.9).
в случае, если группы достатрочно широки, эти отличия сказываются существенно, поэтому пв процессе подготовки констант к расчту в них приходится вводить специальные поправки (см.3.9).
Сечения же, усредняемые с весом, обратным полному макроскопическому сечению, от состава среды могут зависеть весьма существенно. Если в среде присутствует только один резонансный нуклид, эта проблема может быть разрешена следующим образом. Среднегрупповые сечения нерезонансных нуклидов усредняются без учёта резонансной структуры потока (определяющейся множителем 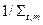 ), т.е. для них принимается
), т.е. для них принимается 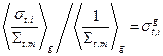 (и аналогично для сечений упругого рассеяния и деления). Для резонансного нуклида кроме того рассчитывается фактор резонансной самоэкранировки зависящий от сечения разбавления этого нуклида всеми остальными нуклидами, входящими в состав среды. В частности, для фактора самоэкранировки полного сечения имеем:
(и аналогично для сечений упругого рассеяния и деления). Для резонансного нуклида кроме того рассчитывается фактор резонансной самоэкранировки зависящий от сечения разбавления этого нуклида всеми остальными нуклидами, входящими в состав среды. В частности, для фактора самоэкранировки полного сечения имеем:
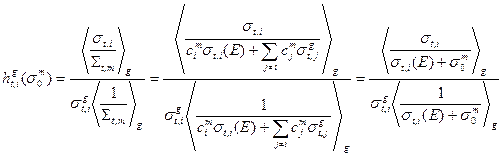 (3.47)
(3.47)
где сечение разбавления есть
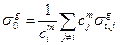 . (3.48)
. (3.48)
Рассчитав факторы самоэкранировки для разных значений сечения разбавления можно будет рассчитать заэкранированное полное сечение резонансного нуклида в любой среде, содержащей кроме него только нерезонансные нуклиды. Коль скоро структура сечений проявляется, главным образом, в форме резонансных пиков, факторы самоэкранировки оказываются меньше единицы: в области резонансных пиков i-го нуклида имеют место пики и в полном мактроскопическом сечении (если концентрация резонансного нуклида в среде не слишком мала) и, следовательно, в плотности нейтронного потока проявляется провал: нейтроны, попавшие в область резонанса, очень быстро покидают эту область в результате столкновений с резонансным нуклидом. В этом и проявляется эффект резонансной самоэкранировки.
Факторы самоэкранировки нередко (особенно за рубежом) называются факторами Бондаренко, в честь Игоря Ильича Бондаренко – выдающегося учёного, по инициативе и под руководством которого была составлена первая версия многогрупповых констант для расчёта реакторов и радиационной защиты[10]
Формализм факторов самоэкранировки открывет возможность учёта зависимости среднегрупповых микроконстант, входящих в уравнение для глобального потока (3.42а), от состава среды, обусловленную резонансной самоэкранировкой. Формулы (3.44) для гомогенной среды фиксированного состава можно теперь переписать в виде
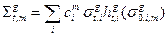 ; (3.49а)
; (3.49а) 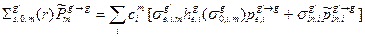 ; (3.49б)
; (3.49б)
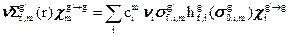 , (3.49в)
, (3.49в)
где все величины, стоящие в правых частях равенств, могут быть вычислены заранее через известные оцененные данные. В формулах (3.49) предполагается, что резонансная самоэкранировка сечений неупругого рассеяния (и, тем более, реакций (n, 2n) и (n, 3n)) несущественна. Зависимость микроконстант от состава среды определяется факторами резонансной самоэкранировки. Сечение разбавления, от которого огни зависят следует рассчитывать по формуле
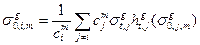 , (3.50)
, (3.50)
учитывающей, что i-й нуклид в среде разбавлен заблокированными сечениями других нуклидов, если они также обладают резонансной структурой. Вычисление сечения разбавления по формуле (3.50) должно производиться итерационно: сначала сечения всех остальныхь нуклидов считаются неблокированными; изатем полученные в этом приближении факторы самоэкранировки используются для уточнения сечений сечения удобно ввести в расчёт сечение поглощения без деления (или «сечение захвата»), и полное сечение рассчитывать как сумму парциальных сечений. В этом случае в наборе микроконстант для каждого нуклида вместо полного сечения вводится сечение захвата 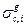 и соответствующий фактор самоэкранировки
и соответствующий фактор самоэкранировки 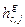 . Факторы резонансной самоэкранировки полного сечения, фигурирующие в формуле (3.50), могут быть выражены через факторы самоэкранировки сечений отдельных процессов:
. Факторы резонансной самоэкранировки полного сечения, фигурирующие в формуле (3.50), могут быть выражены через факторы самоэкранировки сечений отдельных процессов:
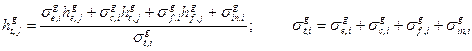 . (3.51а, б)
. (3.51а, б)
Перейдём теперь к оценке сечений групповых констант, фигурирующих в уравнении для тока (3.42б). Эти константы усреднены по энергии с весом тока 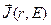 и для оценки формы энергетической зависимости тока необходимо обратиться к уравнению (3.42б). Простейшее приближение, которое можно сделать для оценки резонансной структуры тока состоит в пренебрежении интегральным членом в этом уравнении, т.е. в пренебрежении анизотропией замедления нейтронов. В этом приближении с использованием приближенных выражений, введенных для оценки констант, фигурирующих в уравнении для потока, для гомогенной среды m получаем:
и для оценки формы энергетической зависимости тока необходимо обратиться к уравнению (3.42б). Простейшее приближение, которое можно сделать для оценки резонансной структуры тока состоит в пренебрежении интегральным членом в этом уравнении, т.е. в пренебрежении анизотропией замедления нейтронов. В этом приближении с использованием приближенных выражений, введенных для оценки констант, фигурирующих в уравнении для потока, для гомогенной среды m получаем:
 (3.52)
(3.52)
Используя эту оценку, получаем:
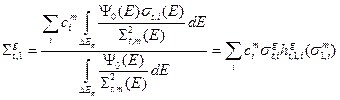 ., (3.53а)
., (3.53а)
 (3.53б)
(3.53б)
где фактор смоэкранировки токового полного сечения определён как
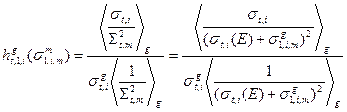 , (3.54)
, (3.54)
где
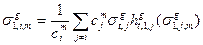 , (3.55).
, (3.55).
- сечение разбавления для токовых членов. Как и сечение разбавления для потоковых членов, оно должно вычисляться итерационно. Фактор самоэкранировки для сечения упругого рассеяния для уравнения (3.42б) определяется аналогично. Средние косинусы угла упругого рассеяния, сопровождающегося замедлением из одной группы в другую, 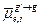 , в рассматриваемом приближении могут быть оценены без учёта резонансной структуры. То же можно сказать и об анизотропии неупругого рассеяния (которая, как правило, мало существенна).
, в рассматриваемом приближении могут быть оценены без учёта резонансной структуры. То же можно сказать и об анизотропии неупругого рассеяния (которая, как правило, мало существенна).
Полученные формулы для расчёта микроскопических групповых констант, как ясно из сказанного выше, базируются на целом ряде приближений и допущений. Применимость этих приближений при расчёте групповых констант весьма продробно проанализирована в монографии[11], к которой мы и отсылаем заинтересованного читателя. Здесь же отметим лишь, что выполненные исследования показали приемлемость совокупности этих приближений для подготовки групповых констант для расчёта энергетических реакторов на быстрых нейтронах, хотя в некоторых случаях при расчёте групповых макроконстант в некоторые из них, как говорилось, порой требуется вводить некоторые поправочные коэффициенты.
Из за допплеровского уширения резонансов, с ростом температуры резонансная структура сечений несколько сглаживается и факторы Бондаренко возрастают. Таким образом, эти факторы должны табулироваться не только в зависимости от сечения разбавления, но также и в зависимости от температуры.
Факторы самоэкранировки Бондаренко наиболее употребительный, но не единственный способ описания резонасной самоэкранировки в многогрупповыхь расчётах. Альтернативой является метод подгрупп, сущность которого состоит в следующем. Пусть в рассматриваемой группе интересующий нас нуклид обладает сложной1 резонансной структурой. Пусть 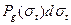 - вероятность того, что нейтрон, попавший в группу будет иметь энергию, при которой полное сечение резонансного нуклида имеет полное сечение от
- вероятность того, что нейтрон, попавший в группу будет иметь энергию, при которой полное сечение резонансного нуклида имеет полное сечение от 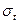 до
до 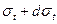 . Тогда если всем остальным нуклидам, входящим в состав среды, можно приписать постоянные среднегрупповые сечения, и если принять, что форма стандартного спектра не влияет на результаты вычисления факторов самоэкрантировки, то интегралы по энергии, стоящие в формулах для факторов самоэкранировки полного сечения можно, можно переписать в виде интегралов Лебега по полному сечению
. Тогда если всем остальным нуклидам, входящим в состав среды, можно приписать постоянные среднегрупповые сечения, и если принять, что форма стандартного спектра не влияет на результаты вычисления факторов самоэкрантировки, то интегралы по энергии, стоящие в формулах для факторов самоэкранировки полного сечения можно, можно переписать в виде интегралов Лебега по полному сечению 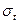 . Например, если принять для простоты
. Например, если принять для простоты 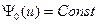 : то формулы (3.45 а, б) можно переписать в виде
: то формулы (3.45 а, б) можно переписать в виде
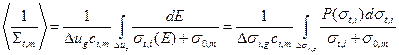 (3.56а)
(3.56а) 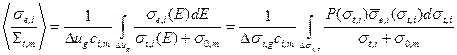 (3.56б)
(3.56б)
Здесь интегрирование по полному сечению i-го нуклида ведётся по всему интервалу его изменения в пределах группы. 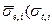 ) – сечение упругого рассеяния, усреднённое по всем энергиям в группе g, в которых полное сечение равно
) – сечение упругого рассеяния, усреднённое по всем энергиям в группе g, в которых полное сечение равно 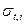 . Лебегова форма интегралов, фигурипующих в формулах (3.45в) и (3.54) записывается аналогично. Лебегова форма записи интегралов целесообразна постольку, поскольку для вероятности
. Лебегова форма интегралов, фигурипующих в формулах (3.45в) и (3.54) записывается аналогично. Лебегова форма записи интегралов целесообразна постольку, поскольку для вероятности 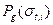 оказывается возможным найти простое приближенное представление. Именно, все нейтроны данной группы разбиваются на несколько подгрупп, каждой из которых приписывается определённое подгрупповое полное сечение
оказывается возможным найти простое приближенное представление. Именно, все нейтроны данной группы разбиваются на несколько подгрупп, каждой из которых приписывается определённое подгрупповое полное сечение 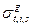 , сечение упругого рассеяния
, сечение упругого рассеяния  и, если нуклид i –делящийся, то и сечение деления
и, если нуклид i –делящийся, то и сечение деления 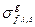 . Индекс s здесь – номер подгруппы. Кроме того, каждой подгруппе пририсывается доля подгруппы
. Индекс s здесь – номер подгруппы. Кроме того, каждой подгруппе пририсывается доля подгруппы 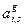 , имеющая смысл вероятности того, что нейтрон, попавший в группу в результате замедления из других групп или в результате рассеяния в ней самой, не приведшего к замедлению из группы, попадёт в подгруппу s, для которой сечениям нуклида i могут быть приписаны соответствующие подгрупповые значения. Другими словами, принимается, что
, имеющая смысл вероятности того, что нейтрон, попавший в группу в результате замедления из других групп или в результате рассеяния в ней самой, не приведшего к замедлению из группы, попадёт в подгруппу s, для которой сечениям нуклида i могут быть приписаны соответствующие подгрупповые значения. Другими словами, принимается, что
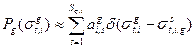 (3.57)
(3.57)
В этом приближении среднегрупповые величины, входящие в формулы для факторов самоэкранировки приобретают вид:
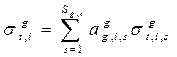 ;
; 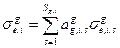 ;
;  (3.58а, б, в)
(3.58а, б, в)
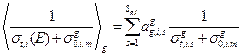 ;
; 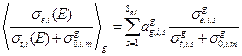 (3.59а, б)
(3.59а, б)
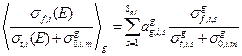 ; (3.59г)
; (3.59г)
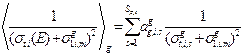 ;
; 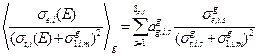 (3.60а, б)
(3.60а, б)
Таким образом, с помощью подгрупповых параметров удаётся весьма просто описать зависимости факторов самоэкранировки от сечений разбавления 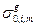 и
и 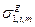 . Сами подгрупповые параметры и подбираются теким образом, чтобы описать эти зависимости с заданной точностью[12]. Оказывается, что для обеспечения максимальной погрешности в факторах самоэкранировки 1% достаточно не более 6 подгрупп, а в области энергий, важной для быстрых реакторов, не более 4 подгрупп.
. Сами подгрупповые параметры и подбираются теким образом, чтобы описать эти зависимости с заданной точностью[12]. Оказывается, что для обеспечения максимальной погрешности в факторах самоэкранировки 1% достаточно не более 6 подгрупп, а в области энергий, важной для быстрых реакторов, не более 4 подгрупп.
Подгрупповое представление резонансной структуры сечений позволяет учитывать резонансную самоэкранировку сечений и в тех случаях, когда пренебрежение токовым членом при оценке формы внутригруппового спектра не оправдано, что имеет место, в частности, вблизи границ раздела сред разного состава. В этом случае резонансная структура плотности потока, очевидно, зависит от координат: с одной стороны от границы на достаточно большом от неё расстоянии (несколько длин свободного пробега), плотность столкновений определяется структурой полного сечения одной среды, а с другой стороны - структурой полного сечения другой среды. Для учёта резонансной самоэкранировки в гетерогенных средах вместо классического многогруппового метода может быть применён метод подгрупп. В этом случае каждая группа при расчёте разбивается на столько частей, сколько в ней подгрупп и решается такая же система уравнений, как и во многогрупповом методе, но с большим числом групп. Существенным отличием является то, что в результате рассеяния в одной из подгрупп нейтрон может попасть в любуюугую подгруппу той же группы между тем как при обычном многогрупповом подходе рассеянные нейтроны либо замедляются в группы с большими номерами, либо остаются в той же группе. Это позволяет рассчитывать потоки нейтронов последовательно, группа за группой, начиная с первой, самой высокоэнергетической, что существенно используется в большинстве программ многогрупповых расчётов. Поэтому эти программы не могут быть автоматически переключены на расчёты в подгрупповом приближении. Легле всего эта проблема решается при решении уравнения переноса методом Монте-Карло, хотя и в этом случае применение метода подгрупп сопряжено с определёнными трудностями, о которых будет сказано ниже.
3. 9. Система групповых констант БНАБ
Первая система групповых констант для расчёта быстрых реакторов, в которой была реализщована описанная выше методика подготовки групповых констант была создана и опубликована в 1962 г.[13] и издана в 1964 г.10. За рубежом по инициалам авторов она получила название ABBN, а в нашей стране – БНАБ. Для отличия от более поздних версий эта версия стала называться БНАБ-64. Более поздними версиями, использовавшимися в инженерной практике, явились БНАБ-78[14] и БНАБ-93[15]. Последняя версия, основанная на библиотеке оцененных данных РОСФОНД, получила название БНАБ-РФ.
Вычисление групповых констант на основе библиотек оцененных нейтронных данных представляет собой достаточно сложную задачу. В конце 50-х – начале 60-х годов, когда создавались первые версии групповых констант для расчёта быстрых реакторов, объём информации о нейтронных данных был невелик, а их погрешности были весьма существеннымы. В этих условиях все необходимые для расчёта констант вычисления могли выполняться вручную с помощью калькуляторов. В 70-х годах полнота и точность оцененных нейтронных данных настолько возрасли, что для их перработки в групповые константы потребовалась разработка специального программного обеспечения. В СССР для создания системы групповых констант БНАБ-78 был создан программый комплекс ГРУКОН[16], обрабатывающего оцененные данные в некотором специальном формате (формате СОКРАТОР), использовавшемся тогда в нашей стране. Позднее, когда во всех странах, в том числе и в СССР, был принят единый формат представления оцененных ENDF, программа ГРУКОН была адаптирована и к этому формату. За рубежом для получения групповых констант повсеместно стал использоваться американский программный комплекс NJOY[17]. Эти комплексы были взаимно проверифицированы. Следует отметить, что грамотное использование упомянутых комплексов требует от расчётчика немалой квалификации, необходимой для того, чтобы правильно установить многочисленные «ручки управления» вычислительным процессов в соответствии с особенностями представления оцененных данных каждого материала.
Система групповых констант БНАБ-64 содержала данные для 26 энергетических групп; в системе констант БНАБ-78 были добавлены ещё две группы при высоких энергиях (нужные для расчёта термоядерных и гибридных реакторов). Границы которых представлены в таблице 3.1. Верхняя граница -1-й группы – 20 МэВ. К 90-му году была создана система констант БНАБ-90. Её окончательная версия, использующаяся и в современных инженерных расчётах быстрых реакторов и защиты, называется БНАБ-93. В этой, так называемой мультигрупповой, системе констант было уже 299 групп: группы БНАБ-78 были разбиты на несколько равных по летаргии частей[18]. Мультигрупповая системы констант, основанная на библиотеке оцененных данных РОСФОНД, получившая название БНАБ-РФ, находится в настояще время (2010г.) в опытной эксплуатации.
Стандартный спектр, принятый при получении групповых констант при энергиях выше 2.5 МэВ представлял собой спектр нейтронов деления в форме Уатта:  , при более низких энергиях – спектр Ферми
, при более низких энергиях – спектр Ферми 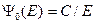 , в 26-й, тепловой, группе – спектр Максвелла с температурой 300К (0.0265 эВ): Как видно из таблицы, деление на группы в области замедляющихся нейтронов принято равномерным в логарифмическом масштабе, что естественно, поскольку потеря энергии при упругом рассеянии пропорциональна энергии рассеянного нейтрона. Каждая декада в этой области разбивалась на три равных части в масштабе летаргии
, в 26-й, тепловой, группе – спектр Максвелла с температурой 300К (0.0265 эВ): Как видно из таблицы, деление на группы в области замедляющихся нейтронов принято равномерным в логарифмическом масштабе, что естественно, поскольку потеря энергии при упругом рассеянии пропорциональна энергии рассеянного нейтрона. Каждая декада в этой области разбивалась на три равных части в масштабе летаргии 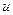 (
(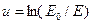 ; Е0=10 МэВ).
; Е0=10 МэВ).
Таблица 3.1. Границы групп 28-групповой разбивки (в элетронвольтах) и число групп мультигрупповой системы в каждой из широких групп.
| № | Е нижн | Число мульти- групп | № | Е нижн | Число мульти- групп | № | Е нижн | Число мульти- групп | № | Е нижн | Число мульти- групп |
| -1 | 13.981*106 | 0.4*106 | 4.67*103 | ||||||||
| 10.5*106 | 0.2*106 | 2.15*103 | 4.67 | ||||||||
| 6.0*106 | 0.1*106 | 1.0*103 | 2.15 | ||||||||
| 4.0*106 | 46.7*103 | 1.0 | |||||||||
| 2.5*106 | 21.5*103 | 0.467 | |||||||||
| 1.4*106 | 10.0*103 | 0.217 | |||||||||
| 0.8*106 | 4.67*103 | 46.7 |
Последние (мультигрупповые) версии констант БНАБ представлены в виде форматированных таблиц. Каждая таблица содержит две стандартных заголовочных строки:
NAM =U238 BIB =FOND MF =301 MT = 0 AWR. = 9.20000E+01
LV = 20 LT = 299 LC = 10 LS = 10 LF = (I2, I3, 8E12.5)
В первой из них указывается стандартное наименование нуклида NAME (как правило, не более чем 4-символьное: NA; FE56; U238; PU39 и т.п.), BIB – наименование библиотеки оцененных данных, на основе которых получены групповые константы, признаки MF и MT, определяющие содержание таблицы данных и, вещественное число, смысл которого зависит от MF и MT (в приведенном примере это отношение массы ядра к массе нейтрона).
Вторая заголовочная строка определяет формат представления данных. LV – признак, определяющий порядок следования целых и вещественных чисел в столбцах (LV=20 означает, что в первых двух столбцах приводятся целочисленные величины, буквенная информация отсутствует). LT – число строк; LC – число столбцов; LS – число строк в одной части таблицы (если таблица разбита на части; в последней версии системы БНАБ всегда LS=LC). LF –формат считывания строк таблицы. Содержание таблицы зависит от MF и МТ.
|
|
