
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Механизмы взаимодействия нейтронов с ядрами
|
|
При энергиях ниже нескольких МэВ определяющими являются следующие два механизма взаимодействия нейтронов с ядрами:
- потенциальное рассеяние (рассеяние на ядре как на упругом теле)
- проникновение нейтрона через поверхность ядра и образование составного ядра.
Составное ядро представляет собой сильно возбуждённый изотоп ядра-мишени. Энергия возбуждения равна
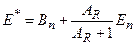 (3.16)
(3.16)
Здесь 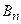 - энергия связи нейтрона в составном ядре,
- энергия связи нейтрона в составном ядре, 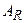 - отношение массы ядра к массе нейтрона (ясно, что
- отношение массы ядра к массе нейтрона (ясно, что 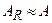 ),
), 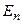 - кинетическая энергия нейтрона. Поскольку нейтрон передал ядру свой импульс, оно движется и его кинетическая энергия равна
- кинетическая энергия нейтрона. Поскольку нейтрон передал ядру свой импульс, оно движется и его кинетическая энергия равна 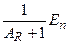 .
.
Благодаря сильному взаимодействию между нуклонами в ядре, энергия возбуждения, внесённая поглотившимся нейтроном, мгновенно, за время порядка 10-20 сек, распределяется между нуклонами в ядре и проходит много большее время прежде чем составное ядро «разрядится» испустив фотон, нейтрон или каким-либо иным способом.
Для того чтобы нейтрон мог образовать составное ядро, это ядро должно иметь энергетический уровень с энергией 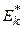 , близкой к энергии
, близкой к энергии 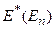 , которую нейтрон вносит в ядро. Близкий – это означает, что разность между этими энергиями не должна существенно превышать ширину уровня
, которую нейтрон вносит в ядро. Близкий – это означает, что разность между этими энергиями не должна существенно превышать ширину уровня  . Кроме того, этот уровень должен обладать спином
. Кроме того, этот уровень должен обладать спином 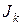 , удовлетворяющим условию
, удовлетворяющим условию 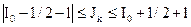 , где l – момент вращения (орбитальный момент), переданный нейтроном ядру при столкновении, а 1/2 =s – спин нейтрона. Кроме того, четность уровня должна удовлетворять условию
, где l – момент вращения (орбитальный момент), переданный нейтроном ядру при столкновении, а 1/2 =s – спин нейтрона. Кроме того, четность уровня должна удовлетворять условию 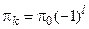 .
.
Если энергия нейтрона невелика, так что его длина волны де-Бройля существенно больше, чем радиус ядра, то нейтрон не может передать ядру момент вращения. В этом случае l =0 и, таким образом, медленные нейтроны могут образовывать составные ядра только в состояниях со спином 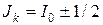 и чётностью
и чётностью 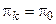 . Взаимодействие, не сопровождающееся передачей орбитального момента принято называть s-взаимодействием.
. Взаимодействие, не сопровождающееся передачей орбитального момента принято называть s-взаимодействием.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Если энергия нейтрона достаточно велика, так что его длина волны де-Бройля становится сравнимой с радиусом ядра, возможно взаимодействие с передачей орбитального момента l =1 (р-взаимодействие). Отношение вероятности р-взаимодействия к вероятности s- взаимодействия определяется так называемым фактором проницаемости, зависящим от соотношения между радиусом канала а и длиной волны де-Бройля и равным для l =1
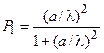 (3.17)
(3.17)
Если принять, что а=R, где R определено согласно (7), то получим, что 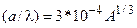 . Обычно для радиуса канала используется формула
. Обычно для радиуса канала используется формула 
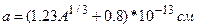 , считающаяся более точной.
, считающаяся более точной.
При высоких энергиях возможно взаимодействие с передачей больших угловых моментов (l =2 – d-взаимодействие, l =3 – f-взаимодействие и т. д.). При энергиях нейтронов порядка 20 МэВ при взаимодействии с тяжелыми ядрами становятся существенными взаимодействия с l до 7 – 9.
Сечение потенциального рассеяния нейтронов описывается довольно простой формулой:
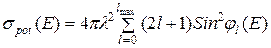 , (3.18)
, (3.18)
где фаза потенциального рассеяния 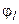 зависит от энергии нейтрона и от орбитального момента l, передаваемого ядру:
зависит от энергии нейтрона и от орбитального момента l, передаваемого ядру:
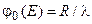 ; (3.19а)
; (3.19а)
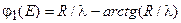 (3.19б)
(3.19б)
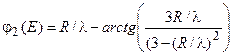 (3.19в)
(3.19в)
Здесь R- радиус ядра (3.14), 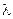 - длина волны де-Бройля (3.12). Из формулы (3.18) следует, что при не слишком высоких энергиях, когда p-рассеяние не существенно и
- длина волны де-Бройля (3.12). Из формулы (3.18) следует, что при не слишком высоких энергиях, когда p-рассеяние не существенно и 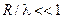 , сечение потенциального рассеяния не зависит от энергии и равно
, сечение потенциального рассеяния не зависит от энергии и равно 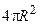 .
.
Упругое рассеяние нейтроновможет происходить как по механизму потенциального рассеяния, так и по механизму образования составного ядра. Энерго-угловое распределение рассеянных нейтронов (в отличие от сечения рассеяния) от механизма не зависит.
Между углом упругого рассеяния и потерей энергии существует однозначная связь, определяемая законами сохранения энергии и импульса. Если угол рассеяния 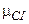 рассматривать в системе центра инерции, связь между энергией Е до рассеяния и энергией E’ после рассеяния очень проста:
рассматривать в системе центра инерции, связь между энергией Е до рассеяния и энергией E’ после рассеяния очень проста:
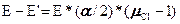 , (3.20)
, (3.20)
где 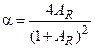 .
.
Зависимость от угла рассеяния в лабораторной системе координат, которая и требуется знать при решении уравнения переноса, более сложна: косинус угла рассеяния в лабораторной системе координат связан с начальной и конечной энергией рассеянного нейтрона и с косинусом угла рассеяния в системе центра инерции соотношениями:
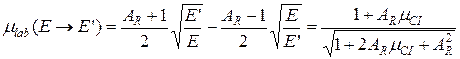 (3.21)
(3.21)
Упругое рассеяние нейтронов с l =0 на всех ядрах изотропно в системе центра инерции. Из формулы (3.20) следует, что в этом случае рассеянные нейтроны распределены равномерно по энергии от 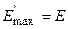 , достигаемого при
, достигаемого при 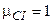 , до
, до 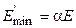 , достигаемого при лобовом столкновении, когда
, достигаемого при лобовом столкновении, когда  . В случае водорода, для которого
. В случае водорода, для которого 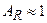 и потому
и потому 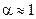 , спектр рассеянных нейтронов распределён равномерно от 0 до начальной энергии нейтронов. При этом, как видно из соотношения (3.21), нейтроны летят только в переднее полупространство:
, спектр рассеянных нейтронов распределён равномерно от 0 до начальной энергии нейтронов. При этом, как видно из соотношения (3.21), нейтроны летят только в переднее полупространство: 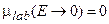 .
.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
В случае водорода рассеяние практически изотропно при любых энергиях, существенных с реакторно-физической точки зрения (т.е. передача орбитального момента протону не происходит). При рассеянии на более тяжелых ядрах р-рассеяние становится существенным уже при энергиях порядка десятков кэВ, а при более высоких энергиях существенно рассеяние с передачей и более высоких угловых моментов. По мере увеличения l угловые распределения рассеянных нейтронов становятся всё более сложными. Например, на рис. 3.2 показано угловое распределение нейтронов с энергией 2.3 МэВ, упруго рассеянных на уране-238. Оцененная кривая, основанная на расчётах, описывающих всю совокупность экспериментальных данных по нейтронным сечениям 238U, сравнивается с экспериментальными данными, полученными одним из экспериментаторов при этой энергии. Как видно, вероятности рассеяния на разные углы различаются до 100 раз. Eсли изображенное на рис.3.2 угловое распределение разложить в ряд по полиномам Лежандра, то для описания его с приемлемой точностью потребуется учёт членов разложения до 8-го порядка включительно. Это говорит о том, что при рассеянии нейтронов рассматриваемой энергии на уране существенны взаимодействия с передачей орбитального момента вплоть до 4-го (можно показать, что максимальный член в разложении по полиномам Лежандра равен 2* l max). Из рассмотрения рис. 3.2 можно сделать вывод, что более ¾ нейтронов этой энергии, рассеивающихся на уране, разлетаются в пределах конуса с углом раствора 45% (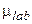 =0.7), т.е. летят преимущественно вперёд и имеют много большую вероятность вылететь из реактора наружу, чем при изотропном рассеянии.
=0.7), т.е. летят преимущественно вперёд и имеют много большую вероятность вылететь из реактора наружу, чем при изотропном рассеянии.
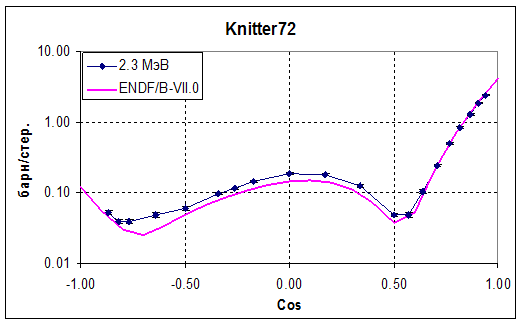
Рис.3.2. Угловое распределение быстрых нейтронов, упруго рассеянных на уране-238
Энергетическая зависимость сечения образования составного ядра весьма сложна. Как говорилось выше, составное ядро может образоваться только при тех энергиях, при которых энергия возбуждения (3.16), передаваемая нейтроном ядру, достаточно близка к уровню составного ядра с подходящими спином и чётностью. На рис. 3.3. приведена энергетическая зависимость полного сечения кислорода при энергиях ниже 4.5 МэВ. Видно, что при энергиях, соответствующих уровням составного ядра – 17О – наблюдаются резкие всплески сечения. Эти энергии отмечены вертикальными линиями. В легенде указывается, каким энергиям возбуждения 17О и каким спинам и чётностям эти уровни соответствуют. Заметим, что первый резонанс – при 0.434 МэВ - соответствует 4-му возбуждённому уровню 17О. Первые три уровня и основное состояние этого ядра лежат ниже энергии связи нейтрона, составляющей 4.143 МэВ.
При низких энергиях полное сечение равно 3.85 барна. Поскольку влияние резонансов при этих энергиях несущественно, это сечение целиком обусловлено потенциальным рассеянием, равным, как отмечалось, 4π R2. Отсюда следует, что радиус ядра кислорода равен 0.554*10-12 см.
Поскольку спин четно-чётного ядра-мишени – 16О –равен нулю, а чётность положительна, резонанс про 434 кэв может образовываться только р-нейтронами, т.е. с передачей орбитального момента l =1 при условии, что этот момент и спин нейтрона s=1/2 сложатся так, чтобы образовать требуемые спин и чётность состояния составного ядра, равные 3/2-. Следующий резонанс может быть только d-резонансом: чтобы чётность была положительной передаваемый ядру момент должен быть чётным. Требуемые спин и чётность – 3/2+ – обеспечиваются вычитанием спина из орбитального момента.
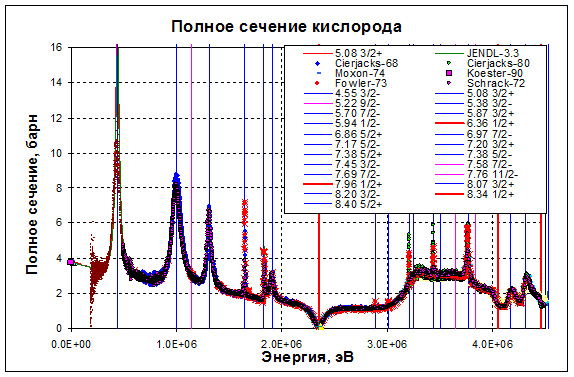
Рис.3.3. Полное сечение кислорода при энергиях ниже 4.5 МэВ
Полное сечение в окрестности изолированного резонансного уровня может быть описано достаточно простой формулой – формулой Брейта-Вигнера:
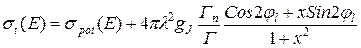 , (3.22)
, (3.22)
Где

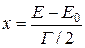 (3.23)
(3.23)
Сечение потенциального рассеяния 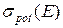 рассчитывается по формуле (3.18).
рассчитывается по формуле (3.18). 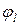 - фаза потенциального рассеяния с угловым моментом l, требующимся для образования составного ядра, рассчитываемого по формулам (3.19).
- фаза потенциального рассеяния с угловым моментом l, требующимся для образования составного ядра, рассчитываемого по формулам (3.19).
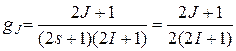 (3.24)
(3.24)
- так называемый статистический фактор, зависящий от спина ядра-мишени I, спина нейтрона s=1/2 и спина того состояния составного ядра, который образуется в рассматриваемом резонансе. Спин J и чётность этого состояния определяют допустимые значения орбитального момента, при которых может образоваться составное ядро. E0 – энергия, соответствующая образованию составного ядра точно при энергии уровня. 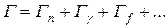 - полная ширина резонансного уровня, представляющая сумму нейтронной ширины
- полная ширина резонансного уровня, представляющая сумму нейтронной ширины 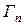 , радиационной ширины
, радиационной ширины 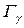 , делительной ширины
, делительной ширины 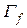 и, возможно ширин для других процессов, которыми составное ядро может снять своё возбуждение. Очевидно, что нейтронная ширина отлична от нуля, т.к. иначе резонанс не образовался бы. Раз составное ядро образовалось, поглотив нейтрон, оно может снять своё возбуждение, снова испустив его. Произойдёт так называемое упругое рассеяние с образованием составного ядра.
и, возможно ширин для других процессов, которыми составное ядро может снять своё возбуждение. Очевидно, что нейтронная ширина отлична от нуля, т.к. иначе резонанс не образовался бы. Раз составное ядро образовалось, поглотив нейтрон, оно может снять своё возбуждение, снова испустив его. Произойдёт так называемое упругое рассеяние с образованием составного ядра.
Всегда отлична от нуля и радиационная ширина, т.к. очевидно, составное ядро всегда имеет возможность перейти в одно из нижележащих возбуждённых состояниё или даже прямо в основное состояние путём испускания гамма-кванта соответствующей энергии (и мультипольности, обеспечивающей необходимое изменение спина). Составные ядра, образующиеся при захвате нейтрона топливными материалами – изотопами тория, урана, плутония – могут снять своё возбуждение путем деления на части (этот процесс будет обсуждён ниже). Возбуждённые состояния составных ядер, образующихся при захвате нейтрона ядрами лития и бора-10, могут снять возбуждение путем испускания альфа-частицы; для них отлично от нуля 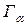 . Возбуждённые состояния 15N, образующиеся при захвате нейтрона в обычном 14N, лежат выше энергии связи протона и для них отлична от нуля протонная ширина
. Возбуждённые состояния 15N, образующиеся при захвате нейтрона в обычном 14N, лежат выше энергии связи протона и для них отлична от нуля протонная ширина 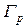 . Чем больше путей распада составного ядра, тем короче его время жизни и – в соответствии с принципом неопределённости (3.15) – тем больше ширина энергетического уровня
. Чем больше путей распада составного ядра, тем короче его время жизни и – в соответствии с принципом неопределённости (3.15) – тем больше ширина энергетического уровня 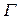 .
.
Сечения парциальных процессов – радиационного захвата, деления и пр., описываются более простыми выражениями, чем полное сечение:
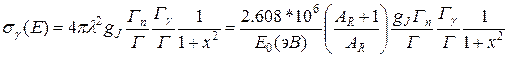 (3.25а)
(3.25а)
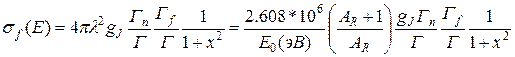 (3.25б)
(3.25б)
Что касается сечения упругого рассеяния, то оно определяется по разности:
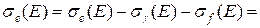
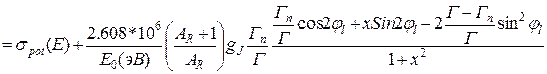 (3.25в).
(3.25в).
Сложный вид последней формулы обусловлен интерференцией нейтронных волн, испускаемых ядром при потенциальном рассеянии и упругом рассеянии с образованием составного ядра. При низких энергиях и(или) при высоких l, когда 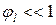 , интерференция не сказывается на форме резонанса в сечении рассеяния. Резонансы в полном сечении в этом случае симметричны (см. рис. 3.3). С ростом энергии интерференция начинает сказываться, прежде всего, на форме s-резонансов. В случае кислорода
, интерференция не сказывается на форме резонанса в сечении рассеяния. Резонансы в полном сечении в этом случае симметричны (см. рис. 3.3). С ростом энергии интерференция начинает сказываться, прежде всего, на форме s-резонансов. В случае кислорода 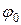 при энергии s-резонанса при 2.35 МэВ фаза потенциального рассеяния для s-волны равна 1.8, т.е близка к
при энергии s-резонанса при 2.35 МэВ фаза потенциального рассеяния для s-волны равна 1.8, т.е близка к 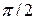 , в связи с чем
, в связи с чем 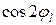 оказывается столь близок к единице, что сечение рассеяния при резонансной энергии падает до 0.11 барна (см. рис.3.3), что на порядок ниже сечения потенциального рассеяния при этой энергии.
оказывается столь близок к единице, что сечение рассеяния при резонансной энергии падает до 0.11 барна (см. рис.3.3), что на порядок ниже сечения потенциального рассеяния при этой энергии.
При низких энергиях, при которых расположены первые резонансы тяжелых ядер, интерференция резонансного и потенциального сечения не играет существенной роли. На рис. 3.4 показан ход полного сечения и сечения захвата урана-238. Резонанс при 6.67 эВ – весьма важен для реакторов на тепловых нейтронах; в нём поглощается львиная доля замедляющихся нейтронов.
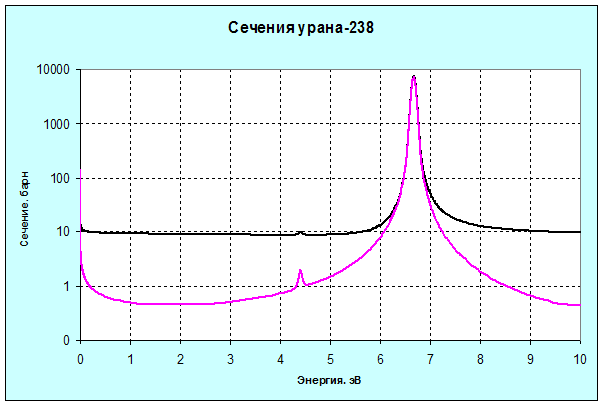
Рис. 3.4. Полное сечение (черная кпивая) и сечение радиационного захвата урана-238 (малиновая кривая) при низких энергиях нейтронов
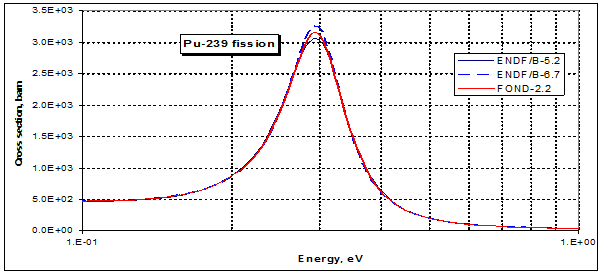
Рис.3.5. Поведение сечения деления плутония-239 при низких энергиях по разным оценкам.
На рис. 3.5 показан ход сечений в области низких энергий для плутония-239. Знаменитый резонанс при 0.3 эВ, определяет большую величину нейтронных сечений при низких – тепловых - энергиях нейтронов. Интересно, что у всех изотопов, делящихся тепловыми нейтронами – 233U, 235U, 241Pu – также имеются резонансы при энергии, близкой к 0.3 эВ.
Нейтронные сечения в максимумах низколежащих резонансов может быть очень большими – достигать миллионов барн. С ростом энергии сечения в максимумах резонансов снижаются.
Резонансные параметры. Положение и форма резонанса определяется значениями нескольких величин – резонансных параметров. К ним относятся:
- Спин и чётность возбуждаемого в резонансе составного ядра Jπ , обычно называемые спином и чётностью резонанса.
- Приведенная нейтронная ширина
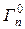 , связанная с нейтронной шириной
, связанная с нейтронной шириной 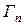 соотношением
соотношением
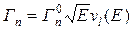 , (3.26)
, (3.26)
где фактор проницаемости 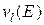 зависит от орбитального момента, который поглощаемый нейтрон должен передать составному ядру:
зависит от орбитального момента, который поглощаемый нейтрон должен передать составному ядру:
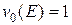 (3.27а)
(3.27а)
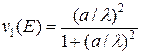 (3.27б)
(3.27б)
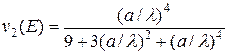 (3.27в)
(3.27в)
Здесь 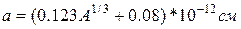 - радиус канала.
- радиус канала.
· Радиационная ширина 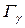
· Делительная ширина 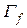 (для ядер, делящихся под действием медленных нейтронов).
(для ядер, делящихся под действием медленных нейтронов).
Подставляя нейтронную ширину (2.26) в формулу Брейта-Вигнера (3.25а, б) для сечения захвата или деления находим, что при E< < E0, когда x< < 1, а 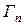 < <
< < 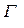 , сечения становятся пропорциональными
, сечения становятся пропорциональными 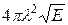 , т.е. обратно пропорциональными
, т.е. обратно пропорциональными 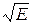 . В этом проявляется так называемый закон 1/v, которому подчиняются сечения захвата и деления при низких энергиях вдали от резонанса.
. В этом проявляется так называемый закон 1/v, которому подчиняются сечения захвата и деления при низких энергиях вдали от резонанса.
Резонансы с одинаковым спином и чётностью образуют систему резонансов. Приведенные нейтронные ширины резонансов одной и той же системы могут очень сильно отличаться от среднего значения: отношения 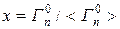 распределены по
распределены по 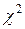 - распределению с одной степени свободы,
- распределению с одной степени свободы,
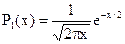 , (3.28)
, (3.28)
что указывает на то, что приведенные нейтронные ширины являются квадратами некоторых величин 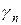 (называемых амплитудами приведенных ширин), которые подчинены нормальному распределению.
(называемых амплитудами приведенных ширин), которые подчинены нормальному распределению.
Резонансы одной и той же системы распределены по энергии не вполне случайно: малые расстояния между ними встречаются редко. Распределение расстояний между резонансами 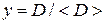 подчиняется распределению Вигнера
подчиняется распределению Вигнера
 (3.29)
(3.29)
В настоящее время определены параметры для очень большого числа резонансов каждого из стабильных ядер. Для урана-238, например, известны параметры примерно 900 s-резонансов и 2400 р-резонансов, лежащих при энергиях до 20 кэВ. При более высоких энергиях лежит область неразрешенных резонансов, в которой резонансная структура сечений также проявляется, хотя и не так сильно, поскольку сечения в максимумах резонансов становятся меньше, и возрастает роль р-, d- и f-резонансов, увеличивающих общую плотность резонансов. Тем не менее, и в области неразрешенных резонансов структура нейтронных сечений может заметно влиять на распространение нейтронов в средах и её необходимо учитывать.
Формула Брейта-Вигнера была получена в предположении, что атомные ядра, с которыми сталкиваются нейтроны, покоятся. Между тем эти ядра находятся в состоянии непрерывного теплового движения и если нейтрон сталкивается с ядром, движущимся ему навстречу, энергия их взаимного движения несколько возрастает, а если нейтрон догоняет ядро, эта энергия чуть снижается. Ясно, что учёт теплового движения ядер должен приводить к некоторому размыванию резонансных пиков, тем большему, чем выше температура среды. Усреднение формулы Брейта-Вигнера по всем возможным скоростям ядра (предполагая, что скорости распределены Максвеллу) приводит к тому, что все множители 1/(1+x2) заменяются на функции 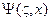 , а множитель x/(1+x2) в (3.25в) заменяется на
, а множитель x/(1+x2) в (3.25в) заменяется на 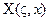 , где параметр
, где параметр 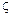 есть отношение полуширины резонанса
есть отношение полуширины резонанса 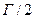 к так называемой доплеровской ширине
к так называемой доплеровской ширине 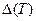 :
:
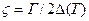 , (3.30)
, (3.30)
где
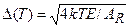 . (3.31)
. (3.31)
Функции 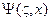 и
и 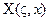 суть вещественная и мнимая части интеграла вероятности от комплексного аргумента z=x+i
суть вещественная и мнимая части интеграла вероятности от комплексного аргумента z=x+i 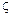 , для которых существуют и таблицы и алгоритмы вычисления.
, для которых существуют и таблицы и алгоритмы вычисления.
Изменение наблюдаемой формы резонанса с ростом температуры среды называют доплеровским уширением.
Следует подчеркнуть, что формула Брейта-Вигнера – простейшая из формул, следующих из строгой формальной теории ядерных реакций. Нетрудно показать, что при рассмотрении нескольких s-резонансов она не всегда обеспечивает даже положительности сечений (за счёт наложения интерференционных минимумов). Более строгой является так называемая многоуровневая формула Брейта-Вигнера, лишенная этого недостатка. Однако, и она не учитывает всех эффектов межрезонансной интерференции, особенно существенных при рассмотрении делящихся ядер, при описании резонансов которых существенен учёт интерференции и делительных ширин. Поэтому при параметризации резонансной структуры делящихся ядер и в ряде других случаев используются еще более сложные резонансные формулы (формула Райха-Мура, формула Адлеров и др.). Несмотря на приближенность, формула Брейта-Вигнера отражает все существенные особенности поведения сечений в окрестности резонанса, важные с точки зрения теории переноса. Поэтому более строгие формулы мы здесь не рассматриваем.
|
|
