Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Макро- и микроскопические константы.

Несмотря на то, что уравнения переноса (3.4) и (3.5) достаточно сложны, современные расчётные методы позволяют их решать сколь угодно точно.

Погрешность решения в этом случае целиком определяется погрешностью коэффициентов этих уравнений – макроскопическими константами. Эти константы определяются концентрациями ядер с_i(r) и микроскопическими сечениями этих ядер. Концентрации ядер в среде известного состава и плотности d вычисляются по хорошо известной формуле:

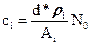, (3.6)

где 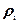- весовая доля нуклида i, A_i – его атомный вес, N₀=6.02242*10²³ – число Авогадро (число молекул в грамм-моле). Под «нуклидом» здесь и далее будем понимать либо изотоп какого-либо элемента, либо природную смесь изотопов, т.е. собственно элемент.

Что касается микроскопических сечений , то таковыми являются площади поперечного сечения атомных ядер. Важнейшая особенность нейтрон-ядерных взаимодействий состоит в том, что одинаковые ядра представляются нейтронам разных энергий объектами совершенно разных размеров, потому и площадь поперечного сечения ядра при нейтронных расчётах приходится считать зависящей от энергии нейтрона..

Макроскопическое полное сечение 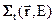, которое было введено в предыдущем параграфе, связано с ядерными концентрациями и поперечными сечениями ядер, входящими в состав среды соотношением:

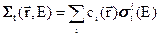. (3.7а)

Таким образом, если мы рассмотрим слой толщиной δ х, то 1 см² этого слоя будет содержать c_idx ядер нуклида i, каждое из которых имеет площадь сечения , так что 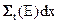- суммарная площадь сечения всех ядер, попавших в рассматриваемый слой. Это рассуждение оправдывает применение к величине 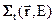, имеющей размерность, обратную длине, название «сечение». Многие авторы трудов по теории переноса вместо 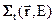оперируют обратной величиной – средней длиной свободного пробега L(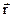, E). Вне зависимости от того, называть величину, обратную средней длине пробега, полным макроскопическим сечением, или нет, соотношение (3.7) связывает с экспериментально измеряемыми микроскопическими сечениями атомных ядер именно эту 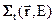=1/L(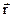, E). Между тем иметь представление о том, каковы длины свободного пробега нейтронов, также важно, чтобы представлять себе, через какие объекты нейтрон может пролететь не столкнувшись, а в каких он наверняка испытает множество столкновений.

Например, для натрия, имеющего на выходе из активной зоны температуру около 800K, плотность равна 0.845 г/см³. При молекулярном весе 23 из формулы (3.6) получаем ядерную плотность 2.2*10²² ядер в см³. Полное сечение взаимодействия быстрых нейтронов с натрием составляет, в среднем, примерно, 4 барна=4*10^-24 см². Отсюда следует, что макроскопическое сечение натрия нейтронов составляет 0.09 см^-1 т.е. длина свободного пробега близка к 10 см. Поскольку заполненные натрием зазоры между тепловыделяющими элементами и между тепловыделяющими сборками существенно меньше длины свободного пробега, эти зазоры почти прозрачны для нейтронов.

Наряду с полным макроскопическим сечением можно ввести макроскопическое сечение упругого рассеяния:

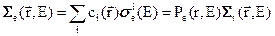, (3.7б)

неупругого рассеяния

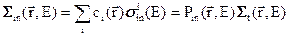, (3.7в)

макроскопические сечения реакций (n, 2n), (n, 3n) и т.п.:

;

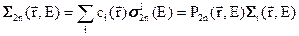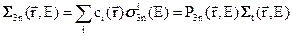. (3.7г)

Через эти величины можно определить вероятность рассеяния, учитывающую вклады всех процессов столкновения, в результате которых появляется один или несколько вторичных нейтронов (кроме процесса деления):

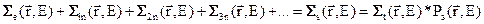(3.8)

Чтобы определить макроскопическую индикатрису рассеяния 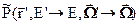, входящую в уравнение переноса, необходимо знать индикатрисы для каждого процесса рассеяния (упругого, неупругого и др.) на каждом ядре. Эти индикатрисы зависят только от косинуса угла рассеяния 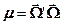, так что

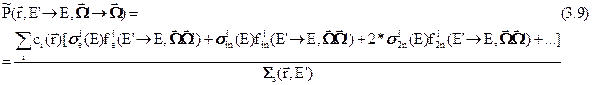Коль скоро макроскопическая индикатриса 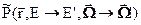учитывает множественность нейтронов, испускаемых при рассеянии (2 в реакции (n, 2n), 3 в реакции(n/3n) и т.д.), интеграл от этой функции по конечным аргументам, вообще говоря превышает единицу и она не может быть интерпретирована как вероятность (что и указывается знаком тильда).

Все процессы, обобщённые под словом «рассеяние» отличаются тем, что образованные в них нейтроны имеют энергию, меньшую, чем нейтрон до рассеяния. Энергетический спектр нейтронов, образующихся при делении, 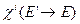довольно слабо зависит от энергии нейтронов, вызывающих деление и поэтому последний интеграл по энергии в уравнении (3.5) берётся по всем возможным энергиям. Макроскопические характеристики среды, входящие в этот интеграл, выражаются через микроскопические характеристики делящихся ядер – сечение сечение деления , среднее число нейтронов, испускаемых при делении и спектр нейтронов деления 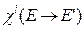– следующим образом:

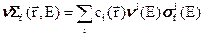. (3.10)

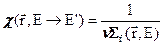
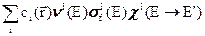. (3.11)

При решении нестационарного уравнения (3.4) требуется знать число как мгновенных 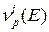, так и всех запаздывающих 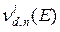нейтронов деления и, соответственно, их спектры 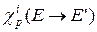и .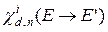

Пространственная зависимость ядерных концентраций (а потому и макроконстант), как правило, кусочно-постоянна. Исключение составляют случаи, когда требуется учитывать изменение нуклидного состава в процессе выгорания, в результате которого состав топливного (или поглощающего) стержня оказывается зависящим от координат. Путем разбиения первоначально однородных материальных зон на части и эта задача сводится к случаю кусочно-постоянных сечений.

Что касается энергетических зависимостей нейтронных сечений и энерго-угловых распределений рассеянных нейтронов, то они чрезвычайно сложны и многообразны и учёт этих зависимостей является фактором, весьма затрудняющим решение уравнения переноса. Характер этих зависимостей и источники данных о нейтронных сечениях будут рассмотрены ниже.