Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Числовые ряды с положительными членами. Теоремы сравнения.

Числовой ряд 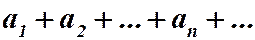называется рядом с положительными членами, если 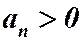при любом п.

Теорема 8. Любой ряд с положительными членами либо сходится, и его сумма есть положительное число, либо расходится и его сумма равна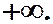

Доказательство. Пусть дан ряд с положительными членами:

.

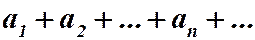Запишем последовательность частичных сумм:

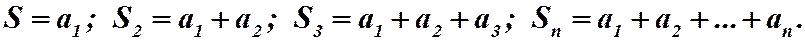
Очевидно, что .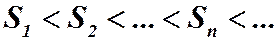

Таким образом, последовательность частичных сумм является строго возрастающей, но тогда возможны два случая:

1) Последовательность частичных сумм 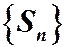ограничена сверху. По теореме Вейерштрасса о пределе монотонной ограниченной последовательности утверждаем, что 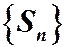имеет конечный предел, то есть ряд сходится.

2) Последовательность частичных сумм 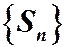возрастает неограниченно, тогда 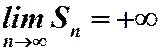, ряд расходится. Теорема доказана.

Признак Коши. Пусть для числового ряда (1) с положительными членами существует предел

σ =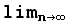

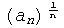
Тогда при σ < 1 ряд сходится, а при σ > 1 ряд расходится.

Можно указать как сходящиеся, так и расходящиеся ряды, для которых σ = 1.

Теорема сравнения. Пусть даны два положительных ряда

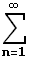
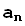(*) и (**)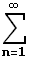

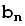Если, начиная с некоторого номера N, т.е. при n > N, выполняется неравенство 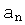≤ 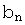, то из сходимости ряда (**) следует сходимость ряда (*), а из расходимости ряда (*) следует расходимость ряда (**).