
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 12. Методы получения регрессионных уравнений
|
|
12.1 Полный факторный эксперимент
Изложение основ факторного планирования эксперимента начнем с простейшего примера.
Пусть имеется две входные переменные Х1 и Х2, одна из которых в интересующей нас области, заштрихованной на рис. 1, а, изменяется в пределах 0, 4  X1
X1  0, 8, а другая — в пределах 10
0, 8, а другая — в пределах 10  X2
X2  30. В процессе проведения эксперимента найдены значения ординат поверхности отклика в граничных точках (рис. 1, а), приведенные в табл. 1.
30. В процессе проведения эксперимента найдены значения ординат поверхности отклика в граничных точках (рис. 1, а), приведенные в табл. 1.
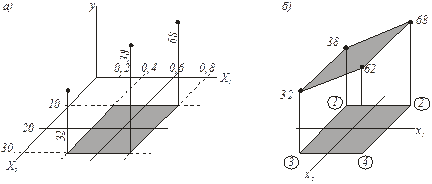
Рис. 1.Полный факторный эксперимент
Поставим задачу поиска аналитического выражения функции отклика в линейной постановке, т.е. дадим приближенное представление этой функции в виде:
 (1)
(1)
Таблица 1
| № точки (опыта) | X1 | X2 | y |
| 0.4 | |||
| 0.8 | |||
| 0.4 | |||
| 0.8 |
Для формализации процедур обработки экспериментальных данных факторы удобно представлять в закодированном виде. С этой целью выберем новую систему координат x1 х2 у (рис. 1, а, 6 ), начало которой совместим с центром интересующей нас области, и назначим масштабы по осям факторов так, чтобы нижний уровень фактора соответствовал ‒ 1, а верхний +1. Это легко достигается с помощью преобразований вида
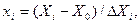 (2)
(2)
где xi – кодированное значение i- ro фактора;
Хi – натуральное значение фактора;
Хо – нулевой уровень;
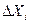 – интервал варьирования фактора.
– интервал варьирования фактора.
Для фактора Х1 нулевой уровень и интервал варьирования будут равны
X10=(0, 4+0, 8)/2=0, 6; 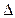 X1 = (0, 8-0, 4)/2=0, 2. Для фактора Х2 имеем: X20=(10 + 30)/2=20;
X1 = (0, 8-0, 4)/2=0, 2. Для фактора Х2 имеем: X20=(10 + 30)/2=20; 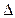 X2 = (30-10)/2=10.
X2 = (30-10)/2=10.
Кодированные значения факторов приведены в табл. 3.2.
В первом и пятом столбцах этой таблицы повторены значения табл. 1. Во втором столбце приведены значения фиктивной переменной x0, характеризующей свободный член bо в уравнении регрессии (1). Значения x 0 всегда принимают равными +1. В 3 и 4 столбцах записаны искомые кодированные переменные; так, для фактора Х1 в первой точке кодированное значение будет x11=( 0, 4 ‒ 0, 6)/0, 2= ‒ 1. Подобные таблицы называют матрицами планирования полного факторного эксперимента.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Таблица 2
| № опыта | X0 | X1 | X2 | Y |
| +1 | -1 | -1 | ||
| +1 | +1 | -1 | ||
| +1 | -1 | +1 | ||
| +1 | +1 | +1 |
Все дальнейшие вычисления полностью формализованы. Коэффициенты регрессии уравнения (3.2) определяют по формуле
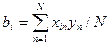 (3)
(3)
где xin – значение xi, в n- ом опыте;
N – число опытов;
уп – значение отклика в n -ом опыте.
Для вычисления коэффициентов регрессии по табличным данным достаточно перемножить данные столбцов у и соответствующих xi, сложить результаты и поделить их на число опытов.
Так, по данным табл. 2 будем иметь

Искомое линейное уравнение поверхности отклика в закодированных переменных будет:
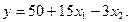
В натуральной (не кодированной) форме это уравнение имеет вид:
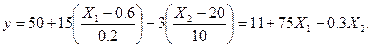 (4)
(4)
Рассмотренный в примере план эксперимента соответствует двум факторам для линейной функции. Если поверхность отклика нелинейна, а вы пытаетесь представить ее приближенное выражение, то в уравнении регрессии (1) следует добавить член b12x1x2, учитывающий взаимодействие факторов х1 и х2. В нашем случае линейной исходной поверхности отклика этот член будет равен нулю, в чем нетрудно убедиться, добавив 6-й столбец, элементы которого равны произведениям элементов 3-го и 4-го столбцов.
В общем случае много факторного эксперимента уравнение регрессии имеет вид:
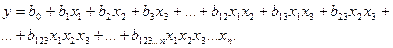 (5)
(5)
Параметр b0 называют общим средним, параметры bi – главными эффектами (взаимодействиями нулевого порядка), параметры bij – эффектами взаимодействия первого порядка (эффектами двухфакторных взаимодействий), параметры bijk – эффектами взаимодействий второго порядка (эффектами трехфакторных взаимодействий) и аналогично b123...n – эффектами взаимодействия порядка п-1 (эффектами n -факторных взаимодействий).
Наиболее часто используют два частных случая функции регрессии: линейную
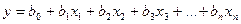 (6)
(6)
и неполную квадратичную
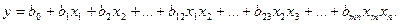 (7)
(7)
Техника эксперимента с варьированием к факторов на двух уровнях сводится к проведению 2k опытов. Для построения матрицы планирования эксперимента при любом к следует дважды повторить матрицу планирования для случая к- 1: один раз для нижнего уровня k -го фактора, а другой раз — для верхнего. Последовательность достраивания матриц планирования при увеличении к от двух до пяти показана в табл. 3. Первые четыре (отчеркнутые) опыта соответствуют двухфакторному эксперименту типа 22, повторяя табл. 2. Восьмифакторный план типа 23 дважды повторяет двухфакторный эксперимент при варьировании третьего фактора сначала на нижнем, а затем на верхнем уровнях. Аналогично строят планы полных факторных экспериментов при других значениях k.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Таблица 3
| № | X0 | X1 | X2 | X3 | X4 | X5 |
| +1 | -1 | -1 | -1 | -1 | -1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | |
| +1 | -1 | +1 | -1 | -1 | -1 | |
| +1 | +1 | +1 | -1 | -1 | -1 | |
| +1 | -1 | -1 | +1 | -1 | -1 | |
| +1 | +1 | -1 | +1 | -1 | -1 | |
| +1 | -1 | +1 | +1 | -1 | -1 | |
| +1 | +1 | +1 | +1 | -1 | -1 | |
| +1 | -1 | -1 | -1 | +1 | -1 | |
| +1 | +1 | -1 | -1 | +1 | -1 | |
| +1 | -1 | +1 | -1 | +1 | -1 | |
| +1 | +1 | +1 | -1 | +1 | -1 | |
| +1 | -1 | -1 | +1 | +1 | -1 | |
| +1 | +1 | -1 | +1 | +1 | -1 | |
| +1 | -1 | +1 | +1 | +1 | -1 | |
| +1 | +1 | +1 | +1 | +1 | -1 | |
| +1 | -1 | -1 | -1 | -1 | +1 | |
| +1 | +1 | -1 | -1 | -1 | +1 | |
| +1 | -1 | +1 | -1 | -1 | +1 | |
| +1 | +1 | +1 | -1 | -1 | +1 | |
| +1 | -1 | -1 | +1 | -1 | +1 | |
| +1 | +1 | -1 | +1 | -1 | +1 | |
| +1 | -1 | +1 | +1 | -1 | +1 | |
| +1 | +1 | +1 | +1 | -1 | +1 | |
| +1 | -1 | -1 | -1 | +1 | +1 | |
| +1 | +1 | -1 | -1 | +1 | +1 | |
| +1 | -1 | +1 | -1 | +1 | +1 | |
| +1 | +1 | +1 | -1 | +1 | +1 | |
| +1 | -1 | -1 | +1 | +1 | +1 | |
| +1 | +1 | -1 | +1 | +1 | +1 | |
| +1 | -1 | +1 | +1 | +1 | +1 | |
| +1 | +1 | +1 | +1 | +1 | +1 |
После выбора факторов для каждого из них следует определить область, ограничивающую их возможное варьирование, и назначить основной уровень. Если, например, по условиям эксперимента нас интересует диапазон температуры воды от 20 до 60°С, то основной уровень (для середины интервала) составит 40°, нижний уровень 20°, верхний уровень 60°С. Разница значений между верхним и нижним уровнями фактора не может быть больше физически возможной. Например, для температуры обычной воды при нормальных условиях эта разность не может превысить 100°С. При этом интервал варьирования не должен быть меньше ошибки фиксирования уровня фактора, иначе верхний и нижний уровни окажутся Факторы, которые по тем или иным причинам невозможно учесть в эксперименте, необходимо во всех опытах стабилизировать на постоянных уровнях.
12.2 Дробный факторный эксперимент
Число опытов в полном факторном эксперименте быстро возрастает с ростом числа факторов. Так, при трех факторах будем иметь 23 = 8 опытов, при 5 факторах – 25 = 32 опыта, а при 8 факторах уже 28 = 256 опытов. Это вызывает необходимость разработки методов отбора части переменных, наиболее существенно влияющих на поверхность отклика. Поэтому, хотя полный факторный план 2k является удобным с точки зрения простоты проведения анализа параметров функции регрессии, тем не менее при большом числе факторов его применяют редко. 0ри трех и более факторах количество опытов можно существенно сократить за счет потери части информации, не очень существенной при построении линейных моделей. Для этого вместо плана 2* следует использовать описанный ниже дробный факторный план 2 k-p (2 k-p  k+ 1), который предназначен для реализации 2 k-p опытов. Для построения дробных планов (реплик) используют матрицы полного факторного эксперимента. Дробные планы создают делением числа опытов полного факторного эксперимента на число, кратное двум. Так получают 1/2 реплики (полуреплику), 1/4 реплики (четвертьреплику) и т. д.
k+ 1), который предназначен для реализации 2 k-p опытов. Для построения дробных планов (реплик) используют матрицы полного факторного эксперимента. Дробные планы создают делением числа опытов полного факторного эксперимента на число, кратное двум. Так получают 1/2 реплики (полуреплику), 1/4 реплики (четвертьреплику) и т. д.
Вначале рассмотрим линейную функцию регрессии, зависящую от трех факторов:
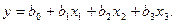 (8)
(8)
Для оценки четырех коэффициентов b0, b1, b2, b3 требуется провести четыре опыта, а проведение полного факторного эксперимента, состоящего из восьми опытов, позволяет несмещенно оценить не только общее среднее b 0 и главные эффекты b1, b 2, b 3, но также и всевозможные взаимодействия первого и второго порядков, т. е. все параметры неполной кубической модели
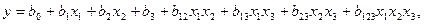 (9)
(9)
содержащей восемь коэффициентов. Следовательно, восемь опытов, поставленных для оценки коэффициентов линейной модели (8), будут содержать в два раза больше информации, чем требуется.
Для оценивания параметров функции регрессии (8) можно построить план, предназначенный для проведения не восьми, а четырех опытов. Для этой цели факторы х1 и х2 следует варьировать, как в плане 22, а в качестве уровня фактора х3 нужно выбрать значение взаимодействия, т.е. х3=х1х2. Получим план, определяемый матрицей, приведенной в табл. 4.
Рассмотрим вопрос построения дробных реплик более подробно. Вернемся к функции регрессии (9). Матрица плана этой модели приведена в табл. 5.
Таблица 4
| № опыта | Матрица плана | |||
| X0 | X1 | X2 | X3 | |
| +1 | +1 | +1 | +1 | |
| +1 | -1 | +1 | -1 | |
| +1 | +1 | -1 | -1 | |
| +1 | -1 | -1 | +1 |
Рассмотрите эту таблицу более внимательно и обратите внимание, что второй столбец таблицы совпадает с девятым, третий — с восьмым, четвертый — с седьмым, пятый — с шестым. Следовательно, при использовании этого плана нет различий между x0 и x1x2x3; x1 и x2x3; х2 и x1x 3; х3 и х1х2, т. е.
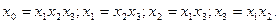 (10)
(10)
На этом основании можно утверждать, что вместо отыскания оценок восьми параметров функции регрессии (3.10) можно найти оценки лишь четырех смешанных коэффициентов:
 (11)
(11)
При этом главные эффекты, включая общее среднее, оцениваются независимо друг от друга, но смешиваются соответственно с эффектами взаимодействий второго и первого порядка. Если постулируется линейная модель (8), то эффекты взаимодействий считаются незначительными, а смешанные коэффициенты (11) превращаются в параметры модели (8).
Таким образом, полный факторный эксперимент 23 при постулировании линейной модели можно рассматривать как совокупность двух полуреплик. Представленный в табл. 5 план называют полурепликой или планом 23-1 полученным из полного факторного плана 23 путем приравнивания единице произведения x1x2x3, т.е.
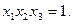 (12)
(12)
Это соотношение называется определяющим для данной полуреплики. Другая полуреплика 23-1 получится из определяющего соотношения x1x2x3, т. е. если уровни фактора х3 устанавливать в соответствии с равенством х3= —x1x2.
Обратите внимание на различие в структуре планов, представленных в табл. 4 и 5 (столбцы 2...4) с одной стороны, и в табл. 3 – с другой. Это различие сделало намеренно и не имеет принципиального значения. Заполнение столбцов 2—5 полного факторного плана может быть произвольным при непременном условии неповторяемости знаков в пределах одной строки. Однако при составлении полуреплик важно, чтобы выполнялось условие (12) или условие х1x2x3= ‒ 1, т. е. для всех опытов данной полуреплики все строки в столбце для x1х2х3 имели одинаковый знак.
Для иллюстрации отмеченных положений рассмотрим конкретный пример. План полного факторного эксперимента и его результаты записаны в левой части (столбцах 1...6) табл. 5. Требуется составить уравнения регрессий для полного факторного эксперимента я для его дробных реплик, если известно, что функция отклика линейна (либо постулируется ее линейность).
Таблица 5
| № опыта | х0 | х1 | х2 | х3 | y | x1x2 | x1x3 | x2x3 | x1x2x3 |
| +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | ||
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | ||
| +1 | -1 | +1 | -1 | -4 | -1 | +1 | -1 | +1 | |
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | ||
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | ||
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | ||
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
Решение. Запишем уравнение регрессии для линейной поверхности отклика
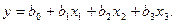 (13)
(13)
Коэффициенты bi будем определять по формуле (3.4) в соответствии с приемами, указанными в пояснениях к этой формуле.
Вначале определим коэффициенты регрессии, используя данные полного факторного эксперимента (левую часть табл. 5). Будем иметь:
 (14)
(14)
Построим дробные реплики, для чего заполним правую часть табл. 5 (столбцы 7...10) и выберем строки, у которых 10-й столбец имеет одинаковые знаки. В результате получим две полуреплики (таблица 6):
Таблица 6
| № опыта | x0 | x1 | x2 | x3 | y |
| Первая полуреплика | |||||
| +1 | +1 | -1 | -1 | ||
| +1 | -1 | +1 | -1 | -4 | |
| +1 | -1 | -1 | +1 | ||
| +1 | +1 | +1 | +1 | ||
| Вторая полуреплика | |||||
| +1 | -1 | -1 | -1 | ||
| +1 | +1 | +1 | -1 | ||
| +1 | +1 | -1 | +1 | ||
| +1 | -1 | +1 | +1 |
Определим коэффициенты регрессии по дробным репликам.
Для первой полуреплики будем иметь:
b0 = (16 ‒ 4 + 8 + 12) / 4 = 8;
b1 = (16 + 4 ‒ 8 ‒ 12) / 4 = 6;
b2 = (-1б ‒ 4 ‒ 8 + 12) / 4=-4;
b3 = (-16 + 4 + 8 + 12) / 4 = 2.
Для второй полуреплики будем иметь
b0=(4 + 8 + 20 + 0) / 4=8;
bl=(-4+8+20-0)/4=6;
b2 =(-4+8-20+0)/4=-4;
b3 = (-4-8 + 20)/4=2.
Как и следовало ожидать, во всех трех случаях для линейной поверхности отклика получены одинаковые результаты.
На рис. 2 приведена схема полного трехфакторного эксперимента и его полуреплик. Цифрами отмечены номера опытов с указанием в скобках координат факторов x1, x2, x3. Точки 2, 3, 5, 8 соответствуют первой полуреплике, а цифры I, 4, 6, 7 – второй. Обратите внимание, что каждая из полуреплик наиболее полно охватывает опытные точки факторного пространства.
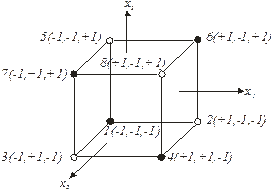
Рис. 2.Схема трехфакторного эксперимента
При большом числе факторов т для оценивания параметров линейной функции регрессии (1) можно строить дробные реплики высокой степени дробности. Так, при т=7 можно построить дробную реплику из полного факторного плана 23 для первых трех факторов, приравняв четыре остававшихся фактора к двухфакторным и трехфакторному взаимодействиям трех других факторов, положив, например
 (15)
(15)
Такую реплику записывают как 27-4.
В общем случае дробную реплику обозначают через 2т-p, если р факторов приравнены к произведениям остальных т—p факторов, уровни которых выбраны согласно полному факторному плану. Дробную реплику 2т-p можно строить различными способами. Для анализа системы смешивания коэффициентов пользуются понятиями генерирующих и определяющих соотношений.
Генерирующими называют соотношения, с помощью которых построена дробная реплика. Так, для реплики, представленной в табл. 5, генерирующим является соотношение х3=x1х2, а это указывает, что фактор х3 занимает в матрице столбец, соответствующий взаимодействию x1x2. Для указанной выше реплики 27-4 генерирующим является соотношение (15).
Определяющим соотношением (определяющим контрастом) называют равенство, в левой части которого стоит единица, а в правой — какое-либо произведение факторов. Для дробной реплики 2т-p можно получить p различных определяющих соотношений из генерирующих путем умножения обеих частей последних на их левые части с последующей заменой (хi)2 на 1 (i= 1,.., т). Другие определяющие соотношения получаются путем перемножения ранее полученных и выделения среди них новых. Например, для реплики (табл. 5) определяющим является соотношение (12).
Построим определяющие соотношения для реплики 27-4, задаваемой генерирующими соотношениями (15). Умножая обе части равенств (15) на их левые части, получаем четыре определяющих соотношения:
 (16)
(16)
Попарное перемножение этих четырех соотношений дает шесть новых:
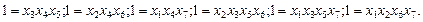 (17)
(17)
Перемножение каждой тройки из четырех соотношений (16) Дает еще три определяющих соотношения:
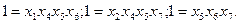 (18)
(18)
Наконец, перемножая все четыре соотношения (16), получаем
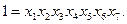 (19)
(19)
Легко понять, что кроме (16) – (19), других определяющих соотношений для рассмотренной реплики 2+7-4 нет.
Знание определяющих соотношений позволяет найти всю систему совместных оценок без изучения матрицы планирования дробной реплики. Для того чтобы определить, с какими взаимодействиями смешано данное, нужно на него умножить обе части всех определяющих соотношений.
Определим, например, с какими взаимодействиями смешан главный эффект b3 в дробной реплике 27-4, определяемой генерирующими соотношениями (15). Для этого умножим все определяющие соотношения (16) – (19) на х3. Получим
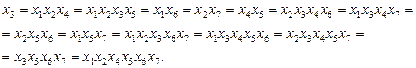

Следовательно, главный эффект b3 смешан с эффектами взаимодействий первого порядка 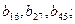 с эффектами взаимодействий второго порядка
с эффектами взаимодействий второго порядка 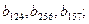 третьего порядка
третьего порядка 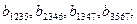 четвертого порядка
четвертого порядка 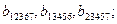 и пятого порядка
и пятого порядка 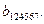
В конкретной практической ситуации для выбора подходящей дробной реплики полного факторного плана необходимо использовать все априорные сведения теоретического и интуитивного характера об объекте планирования с целью выделения тех факторов и произведений факторов, влияние которых на результаты измерений существенно. При этом смешивание нужно производить так, чтобы общее среднее b0 и главные эффекты b1,..., bm были смешаны с эффектами взаимодействий самого высокого порядка (так как обычно они отсутствуют) или с эффектами таких взаимодействий, о которых известно, что они оказывают несущественное влияние на результаты измерений. Отсюда следует, в частности, что недопустимо произвольное разбиение полного факторного плана 23 на две части для выделения полуреплики 23-1.
Качество дробного факторного плана иногда характеризуют с помощью разрешающей способности плана, которая равна наименьшему числу символов в правых частях определяющих соотношений. В частности, для плана разрешающей способности III ни один главный эффект не смешан ни с каким другим главным эффектом, но главные эффекты смешаны с эффектами двухфакторных взаимодействий. Для плана разрешающей способности IV главные эффекты не смешаны друг с другом и с эффектами двухфакторных взаимодействий, но последние друг с другом смешаны. Для плана разрешающей способности V главные эффекты и эффекты двухфакторных взаимодействий не смешаны, но последние смешаны с эффектами трехфакторных взаимодействий. Все три рассмотренные выше дробные реплики имеют разрешающую способность III.
12.3 Метод наименьших квадратов
Рассмотрим особенности регрессионного анализа результатов моделирования на примере построения линейной регрессионной модели.
На рис. 3.9 показаны точки (xi, yi), полученные в эксперименте. Делаем предположение, что функция отклика может быть представлена в виде прямой линии
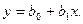
Требуется получить такие значения коэффициентов b0 и b1, при которых сумма квадратов ошибок будет минимальной. На рисунке ошибки ei для каждой экспериментальной точки равны расстояниям по вертикали от этой точки до линии регрессии (рис. 3).
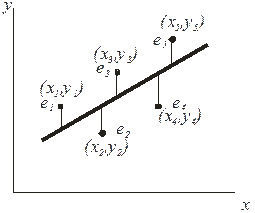
Рис. 3.К построению регрессионной модели
Обозначим (yt)i =b 0 + b0xi ( здесь (уt) i ‒ величина, предсказываемая регрессионной моделью), тогда выражение для ошибок будет иметь вид 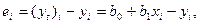 а функция ошибки
а функция ошибки
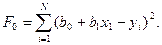
Для получения коэффициентов b0 и b1 при которых функция F0 будет минимальной, приравняем нулю частные производные dF0 /db0 и dF0 /db1. Будем иметь:
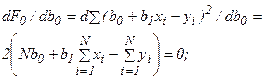
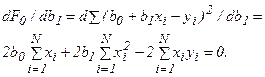 (20)
(20)
Таким образом, получена система двух линейных алгебраических уравнений:
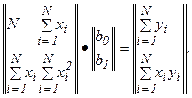 (21)
(21)
Решая систему этих уравнений, получим
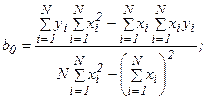
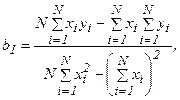 (22)
(22)
где N – число реализаций при моделировании.
Мы рассмотрели частный случай для уравнения (22). В более общем случае, когда эмпирическую функцию принимают в виде полинома
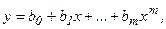 (23)
(23)
система уравнений типа (22), (23) будет иметь вид


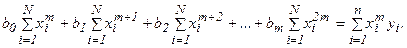 (24)
(24)
Для оценки точности совпадения теоретических и экспериментальных данных следует определить среднюю квадратичную ошибку на единицу веса
 (25)
(25)
или среднее абсолютное отклонение
 (26)
(26)
где r – число вычисляемых (табличных) значений;
s – число параметров.
Последовательность вычислений при построении уравнения регрессии на основе метода наименьших квадратов рассмотрим на конкретном примере.
Пусть например необходимо подобрать уравнение регрессии по экспериментальным данным, приведенным ниже.
| x | 0.5 | 1.0 | 1.5 | 2.0 | |
| y | 7.0 | 4.8 | 2.8 | 1.4 |
Вначале попытаемся в качестве типа эмпирической формулы принять линейную зависимость, удерживая в формуле два первых члена:
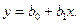
Составим нормальные уравнения, для чего предварительно заполним таблицу В таблице предусмотрим дополнительные столбцы 4, 5 и 8, которые нам могут потребоваться в дальнейшем (таблица 7).
Таблица 7
| x0 | x | x2 | x3 | x4 | y | xy | x2y |
| 7.0 | |||||||
| 0.5 | 0.25 | 0.125 | 0.0625 | 4.8 | 2.4 | 1.2 | |
| 1.0 | 2.8 | 2.8 | 2.8 | ||||
| 1.5 | 2.25 | 3.375 | 5.0625 | 1.4 | 2.1 | 3.15 | |
| 2.0 | |||||||
| 7.5 | 12.5 | 22.125 | 7.3 | 7.15 |
Пользуясь данными столбцов 1, 2, 3, 6, 7, составим нормальные уравнения (3.26), которые применительно к нашему случаю при удержании только двух первых членов формулы будут иметь вид:
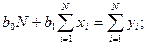

Подставляя табличные данные, получим:

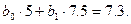
Решая эти уравнения, найдем: b0 = 6, 68; b1 = -3, 48, следовательно,
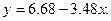
Оценим точность выполненных построений. Подставив в полученную формулу значения x (табл. 8), определим вычисленные значения уt и отклонения.
Таблица 8
| x | yt | y-yt | (y-yt)2 |
| 0.5 1.0 1.5 2.0 | +6.68 +4.94 +3.20 +1.46 -0.28 | +0.32 -0.14 -0.40 -0.06 +0.28 | 0.1024 0.0196 0.1600 0.0036 0.0784 |
Суммируя данные последнего столбца, будем иметь:
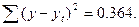
Средняя квадратическая ошибка на единицу веса
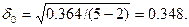
Среднее абсолютное отклонение (5.9) равно
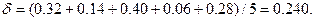
Полученные величины показывают, что формула подобрана неудовлетворительно, так как исходные данные имеют точность до 0, 1, а средняя квадратическая ошибка на единицу веса значительно больше 0, 1.
Повторим все операции, используя более точное выражение
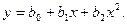
Для записи нормальных уравнений (7) дополним вспомогательную табл. 3.8 новыми данными, которые приведены в столбцах 4, 5, 8 и выделены курсивом. Составим нормальные уравнения:
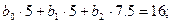
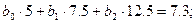
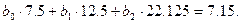
После решения этой системы найдем b0 =7.00; b1 =-4.74; b2 =0.63 и запишем искомую зависимость:

Для определения средней квадратической ошибки составим табл. 9.
Таблица 9
| x | yt | y-yt | (y-yt)2 |
| 0.5 1.0 1.5 2.0 | 7, 0 4.79 2, 89 1.30 0.04 | +0.01 -0.09 +0.10 -0.04 | 0.0001 0.0081 0.0100 0.0016 |
Суммируя последний столбец, получим
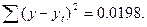
Средняя квадратическая ошибка на единицу веса
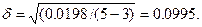
Среднее абсолютное отклонение
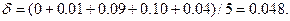
Следовательно, формула 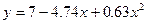 вполне удовлетворительно соответствует экспериментальным данным.
вполне удовлетворительно соответствует экспериментальным данным.
Литература
1. Ильина Н.В. Системный анализ и моделирование процессов в техносфере: Учеб. пособие / Н.В. Ильина, Д.Д. Лапшин, В.И. Федянин. – Ч. 1. Воронеж: ГОУВПО «Воронежский государственный технический университет, 2008. – 206 с.
|
|
