
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 9. Теория игр
|
|
9.1 Конфликт ‒ предмет рассмотрения теории игр
В природе и обществе часто встречаются явления, в которых те или иные участники имеют несовпадающие интересы и располагают различными путями для достижения своих целей. Такие явления называются конфликтами. Конфликты являются предметом рассмотрения теории игр.
Под конфликтом будем понимать всякое явление, применительно к которому можно говорить:
1) кто и как в этом явлении участвует;
2) каковы возможные исходы этого явления;
3) кто в этих исходах заинтересован и в чем эта заинтересованность состоит.
Рассмотрим возможные причины возникновения конфликтов.
Одна из характерных черт всякого общественного, социально-экономического явления состоит в множественности, многосторонности интересов и в наличии сторон, выражающих эти интересы.
Например:
1) продавец и покупатель, имеющие противоположные интересы;
2) несколько производителей, фигурирующих на рынке и обладающих достаточной силой воздействия на цену товара, имеющих в связи с этим как противоположные, так и совпадающие интересы;
3) объединения или коалиции лиц, участвующих в столкновении интересов, как в случаях определения ставок заработной платы союзами или объединениями рабочих и предпринимателей, голосования в парламенте и т. д.
Конфликт может возникать также из различия целей, которые отражают не только несовпадающие интересы, но многосторонние интересы одного и того же лица. Например:
- конструктор согласует противоречивые технико-экономические требования в процессе конструирования изделия: минимизация габаритов, минимизация стоимости, максимизация надежности, простота в обращении;
- разработчики экономической политики согласуют противоречивые требования, предъявляемые к ситуации: рост объемов производства, повышение доходов, снижение экологической нагрузки и т. д.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Конфликт может проявиться не только в результате сознательных действий различных участников, но и как результат действия тех или иных «стихийных сил» (случай так называемых «игр с природой»).
Прямо противоположные интересы различных сторон явно проявляются в непосредственной борьбе: военной, дипломатической, экономической, спортивной.
Наконец, примерами конфликтных ситуаций являются обычные игры: салонные, карточные, шахматные, морской бой и т. д. Для конфликта характерно следующее:
- ни один из его участников заранее не знает решений, принимаемых остальными участниками, т.е. вынужден действовать в условиях неопределенности;
- ход событий в конфликте зависит от решений, принимаемых каждой из сторон, поэтому поведение любого участника конфликта, если оно разумно, должно определяться с учетом возможного поведения всех его участников.
Подводя итог сказанному, отметим, что общим, объединяющим все конфликты, независимо от их физической и социальной природы, является:
1) столкновение интересов нескольких (двух или более) сторон, в том числе сознательных индивидуумов или природы;
2) преследование сторонами различных целей;
3) наличие наборов альтернатив для достижения этих целей, каждая из которых приводит к одному (или к одному из нескольких) возможных исходов.
9.2 Понятие игры. Классификация игр. Формальное представление игр
Игрой называется математическая модель конфликта.
Математическая модель конфликта должна отражать присущие ему черты, а значит, должна описывать:
- множество заинтересованных сторон (игроков);
- возможные действия каждой из сторон (стратегии и ходы);
- интересы сторон, представленные функциями выигрыша (платежа) для каждого из игроков.
В теории игр предполагается, что функции выигрыша и множество стратегий, доступных каждому из игроков общеизвестны, т.е. каждый из игроков знает свою функцию выигрыша и набор имеющихся в его распоряжении стратегий, а так же функции выигрыша и стратегии всех остальных игроков. В соответствии с этой информацией каждый из игроков организует свое поведение.
Различные виды игр можно классифицировать следующим образом:
- по числу игроков;
- по числу стратегий;
- по свойствам функции выигрыша;
- по возможности предварительных переговоров и взаимодействия между игроками в ходе игры.
По числу игроков различают игры с двумя, тремя и более участниками. В принципе возможны так же игры с бесконечным числом игроков.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
По числу стратегий различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий. Например, в игре в орлянку у игроков по две стратегии ‒ «орел» или «решка». В бесконечных играх игроки имеют бесконечное число возможных стратегий. Например, при взаимодействии продавца и покупателя каждый из игроков может назвать любую цену и любое количество продаваемого (покупаемого) товара.
По свойствам функции выигрыша различают игры:
- с нулевой суммой, когда выигрыш одного игрока равен проигрышу другого, т.е. налицо прямой конфликт между игроками;
- с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно, так что им выгодно действовать сообща;
- с ненулевой суммой, где есть и конфликты, и согласованные действия игроков.
По возможности предварительных переговоров и взаимодействия между игроками в ходе игры различают кооперативные и некооперативные игры. Игра называется кооперативной, если до начала игры игроки образуют коалиции и принимают взаимообязывающие соглашения о своих стратегиях (например, образование коалиций в парламенте перед голосованием по некоторым вопросам).
Игра, в которой игроки не могут координировать свои стратегии подобным образом, называется некооперативной (например, все игры с нулевой суммой).
Рассмотрим примеры формального представления игр.
Обозначим через I множество всех игроков, через St ‒ множество возможных действий игрока i 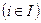 , называемое множеством стратегий.
, называемое множеством стратегий.
Например:
а) игра в орлянку
I = {1, 2}, Sf = {Орел, Решка};
б) голосование в парламенте
I = {1, 2,..., n},
где n ‒ число голосующих, Si = {За, Против, Воздержался};
в) взаимодействие на рынке двух продавцов
I = {1, 2} Si = {Pi: Pi > 0},
где Pi ‒ цена продаваемого товара.
В партии игроки выбирают каждый свою стратегию 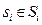 , в результате чего складывается набор стратегий s = (s1, s2, …, sn), называемый ситуацией.
, в результате чего складывается набор стратегий s = (s1, s2, …, sn), называемый ситуацией.
В рассмотренных выше примерах приведем возможные ситуации:
а) (Орел, Орел), (Орел, Решка), (Решка, Орел), (Решка, Решка);
б) (За, За, Против, За, Воздержался, …, Против);
в) (5 рублей, 3 рубля), (5 рублей, 7 рублей).
Заинтересованность игроков в конкретных ситуациях проявляется в том, что каждому игроку i в каждой ситуации s присваивается число, выражающее степень удовлетворения его интересов в данной ситуации. Это число называется выигрышем игрока i и обозначается Нi(s).
Вернемся к указанным выше примерам.
В игре в орлянку.
Н1(Орел, Орел) = Н1(Решка, Решка) = 1,
Н1(Орел, Решка) = Н1 (Решка, Орел) = -1,
Н2(Орел, Орел) = Н2(Решка, Решка) = -1,
Н2(Орел, Решка) = Н2(Решка, Орел) = 1.
Видно, что в любой ситуации Н1 + Н 2 = 0.
Запишем это в виде матрицы выигрышей, где строки будут соответствовать стратегиям 1-го игрока, столбцы ‒ стратегиям 2-го игрока.
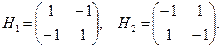
При этом или Н1 + Н 2 = 0.
Таким образом, орлянка является примером игры с нулевой суммой.
При голосовании в парламенте считается, что вопрос прошел при большем количестве проголосовавших «За», чем «Против», в противном случае – вопрос не прошел. Получаем:

В случае взаимодействия на рынке двух продавцов предположим, что потребитель приобретет товар у фирмы, объявившей меньшую цену, или распределит свой спрос поровну между фирмами в случае, если цены равны.
Если d(p) ‒ функция спроса в зависимости от цены на товар, то функция выигрыша.
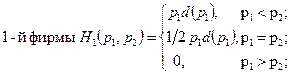
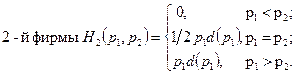
9.3 Определение бескоалиционной игры
Бескоалиционной игрой будем называть такую игру, в которой целью каждого игрока является получение по возможности большего индивидуального выигрыша.
Обозначим.
I ‒ множество всех игроков. Далее будем считать I конечным. Обычно принято различать игроков по номерам, т.е. считать I = {1, 2,..., n };
Si ‒ множество стратегий игрока 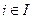 , т.е. множество возможных действий, имеющихся в распоряжении игрока i. Считается, что Si содержит не менее двух возможных стратегий, иначе его действия заранее определены.
, т.е. множество возможных действий, имеющихся в распоряжении игрока i. Считается, что Si содержит не менее двух возможных стратегий, иначе его действия заранее определены.
Процесс игры состоит в выборе каждым из игроков одной своей стратегии 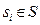 . Таким образом, в результате каждой партии игры складывается система стратегий s = (s1, s2,..., sn), которая называется ситуацией.
. Таким образом, в результате каждой партии игры складывается система стратегий s = (s1, s2,..., sn), которая называется ситуацией.
Множество всех ситуаций S=S1× S2× …× Sn, т.е. S является декартовым произведением множеств стратегий всех игроков. Обозначим: Hi(s) ‒ выигрыш игрока i в ситуации s. Функция Hi, определенная на множестве всех ситуаций, называется функцией выигрыша игрока i.
Hi: S → R, т.е. каждой ситуации 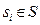 Hi ‒ сопоставляет вещественное число.
Hi ‒ сопоставляет вещественное число.
Бескоалиционной игрой называется система 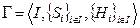 , в которой I и Si (
, в которой I и Si (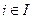 ) являются множествами, а Hi ‒ функции на множестве S=S1× S2× …× Sn, принимающие вещественные значения.
) являются множествами, а Hi ‒ функции на множестве S=S1× S2× …× Sn, принимающие вещественные значения.
Бескоалиционная игра 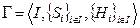 называется игрой с постоянной суммой, если существует такое постоянное число C, что
называется игрой с постоянной суммой, если существует такое постоянное число C, что 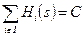
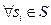 , т.е. сумма выигрышей игроков постоянна в любой ситуации.
, т.е. сумма выигрышей игроков постоянна в любой ситуации.
9.4 Приемлемые ситуации и ситуации равновесия
Ситуацию s в игре Г естественно считать приемлемой для игрока i, если этот игрок, изменяя в ситуации s свою стратегию на какую-либо другую, не может увеличить этим своего выигрыша.
Пусть s = (s1, s2,..., si-1, si, si+1,..., sn) ‒ произвольная ситуация в игре, а si ‒ некоторая стратегия игрока i.
Рассмотрим новую ситуацию 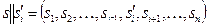 , получившуюся из ситуации s заменой стратегии si игрока i на s'i. Очевидно, что s||s'i = s, если s'i совпадает с si (s'i = si).
, получившуюся из ситуации s заменой стратегии si игрока i на s'i. Очевидно, что s||s'i = s, если s'i совпадает с si (s'i = si).
Ситуация s в игре Г называется приемлемой для игрока i, если 

Смысл названия «приемлемая» состоит в том, что, если в некоторой ситуации s для игрока i найдется такая стратегия s΄ i, что  то игрок i в случае складывающейся ситуации s может получить больший выигрыш, выбирая s΄ i, вместо si. В этом смысле ситуация s для игрока может считаться неприемлемой.
то игрок i в случае складывающейся ситуации s может получить больший выигрыш, выбирая s΄ i, вместо si. В этом смысле ситуация s для игрока может считаться неприемлемой.
Ситуация s называется ситуацией равновесия (или равновесной ситуацией), если она приемлема для всех игроков, т.е. 


Из определения видно, что в ситуациях равновесия и только в них ни один игрок не заинтересован в отклонении от своей стратегии.
Равновесной стратегией игрока в бескоалиционной игре называется такая его стратегия, которая входит хотя бы в одну из равновесных ситуаций игры.
Процесс нахождения ситуаций равновесия в бескоалиционной игре называется решением игры.
9.5 Примеры игровых задач
«Дилемма заключенных»
Предположим, игроками 1 и 2 являются преступники, находящиеся в предварительном заключении по подозрению в тяжком преступлении. Прямых улик против них нет, и возможность их обвинения в значительной мере зависит от того, сознаются ли преступники сами.
Судья предложил каждому следующую сделку. Если он сознается в преступлении, а другой нет, то сознавшийся получает 1 год наказания, а несознавшийся – 10 лет. Если сознаются оба, то каждый получит по 7 лет. Заключенным известно, что если никто из них не сознается, то оба получат по 3 года.
Запишем функции выигрышей (потерь) игроков в рассмотренной игре.
Пусть П – признание, Н – непризнание, H1 – выигрыш 1-го игрока, H2 – выигрыш 2-го игрока.
H1 (П, П) = H2 (П, П) = -7,
H1 (Н, Н) = H2 (Н, Н) = -3,
H1 (П, Н) = H2 (Н, П) = -1,
H1 (Н, П) = H2 (П, Н) = -10.
Игру можно представить с помощью следующей матрицы, в клетках которой слева вверху стоит выигрыш первого заключенного, а справа внизу – второго.
| Второй игрок | |||
| сознаться | не сознаваться | ||
| Первый игрок | сознаться | -7 -7 | -1 -10 |
| не сознаваться | -10 -1 | -3 -3 |
Ситуацией равновесия в данной игре оказывается ситуация, в которой каждый из игроков должен признаться. Тогда каждый из игроков теряет 7, т.е. оказывается осужденным на 7 лет.
В ситуации же, когда ни один не признался, потери каждого всего 3 (каждый осужден на 3 года). Однако данная ситуация явно не устойчива, так как каждый из игроков заинтересован отклониться от выбранной стратегии и признаться, рассчитывая свалить вину на другого и избежать наказания, сведя свои потери к 1 (1 год осуждения, при этом потери партнера составят 10).
Таким образом, разумной стратегией для каждого игрока является признание, так как оно гарантирует игроку неполучение максимального срока в 10 лет. Хотя более выгодной кажется тактика непризнания, дающая возможность получения незначительного наказания (срок в год), однако чревата неожиданностью в виде максимального срока в 10 лет в случае признания со стороны соучастника.
«Обмен закрытыми сумками»
Два человека встречаются и обмениваются закрытыми сумками, понимая, что одна из них содержит деньги, другая — товар. Каждый игрок может уважать сделку и положить в сумку то, о чём договорились, либо обмануть партнёра, дав пустую сумку.
В этой игре обман всегда будет наилучшим решением, означая также, что рациональные игроки никогда не будут играть в неё, и что рынок обмена закрытыми сумками будет отсутствовать.
В вариации, популярной у программистов и хакеров, каждый агент этой игры помнит предыдущие результаты (или имеет доступ к общественному мнению, «коллективной памяти»), и множество обменов повторяются длительное время.
Как отмечено выше, без памяти эта игра имеет мало смысла, она мало что объясняет в поведении систем и групп людей, кроме описания взаимодействий, которые не будут происходить.
Программисты и математики утверждают, что стратегия «око за око» наилучшая общая стратегия
Примеры с заключёнными, карточной игрой и обменом закрытыми сумками могут показаться надуманными, но на самом деле есть множество примеров взаимодействия людей и животных, имеющие такую же матрицу выигрышей.
В политологии, к примеру, сценарий ДЗ часто используется для иллюстрации проблемы двух стран, вовлечённых в гонку вооружений. Обе будут заявлять, что у них есть две возможности: либо увеличить расходы на военные нужды, либо сокращать вооружения. Ни одна из сторон не может быть уверена, что другая будет соблюдать договорённость, следовательно, обе будут стремиться к военной экспансии. Это можно считать теоретическим объяснением политики устрашения. Похожие явления наблюдаются и в автоспорте — «Формула-1», где последние 20 лет происходит гонка бюджетов команд. Из-за этого число машин-участников сократилось с 36 в 1990 году до 20 в 2003.
В велогонках дилемма заключённого возникает, когда два сильных гонщика оторвались от общей группы. Каждый из них может либо предоставить соседу сотрудничество, либо ехать сзади. Для обоих идеалом будет, когда они по очереди «висят» друг у друга на хвосте — но всегда есть желание не дать соседу преимущества (тогда тот постепенно устаёт и «скатывается» в пелотон, а ты финишируешь с большим отрывом).
Случай дилеммы заключённого может быть найден в бизнесе. Две конкурирующие фирмы должны определиться, сколько средств тратить на рекламу. Эффективность рекламы и прибыль каждой фирмы уменьшается с ростом расходов на рекламу у конкурента. Обе фирмы принимают решение увеличить расходы на рекламу, при этом их доли рынка и, возможно, объёмы продаж остаются неизменными, а прибыль сокращается. Предел гонки рекламных бюджетов — прибыль, впрочем, они могут пытаться некоторое время работать и в убыток. Фирмы могут пойти на соглашение о сокращении расходов на рекламу, но всегда есть стимул его нарушить.
В олигополистических рынках ценовая политика — это повторяющаяся ДЗ. Обычно олигополисты сотрудничают друг с другом и не доводят ситуацию до «ценовой войны».
Уильям Паундстоун в книге о дилемме заключённого описывает ситуацию в Новой Зеландии, где газетные ящики оставляют открытыми. Газету можно взять, не заплатив за неё, но мало кто так делает, потому что большинство осознаёт вред, который был бы, если бы все воровали газеты. Поскольку ДЗ в чистом виде одновременна для всех игроков (никто не может повлиять на решения других), эта распространённая линия рассуждений называется «магическое мышление».
Теоретическое заключение ДЗ — одна из причин, почему во многих странах сделка о признании вины запрещена. Часто сценарий ДЗ повторяется очень точно: в интересах обоих подозреваемых сознаться и свидетельствовать против другого подозреваемого, даже если оба невиновны. Возможно, наихудший случай — когда только один виноват, в этом случае невиновный вряд ли сознаётся в чём либо, а виновный пойдёт на это и даст показания против невиновного.
Многие дилеммы в реальной жизни включают множество игроков. Хотя и метафорическую, «трагедию общин» Ардена можно рассматривать как обобщение ДЗ для множества игроков. Каждый житель общины выбирает — пасти ли скот на общем пастбище и получить выгоду, истощая его ресурсы, либо ограничить свой доход. Коллективный результат от всеобщего (или частого) максимального использования пастбища — низкий доход (ведущий к разрушению общины). Однако такая игра не является формальной, поскольку может быть разбита на последовательность классических игр с 2 участниками.
|
|
