Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Лекция 10. Моделирование на основе орграфов
|
|
10.1 Граф и его виды
Первая работа по теории графов принадлежит Леонарду Эйлеру (1736 год), хотя термин «граф» впервые ввел в 1936 году венгерский математик Денеш Кениг. Графами были названы схемы, состоящие из точек (вершины графа) и соединяющих эти точки отрезков прямых или кривых (ребра графа) (рис. 1).
Рис. 1. Примеры графов
С помощью графов часто упрощалось решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. С помощью графов изображаются схемы дорог, газопроводов, тепло- и электросети. Помогают графы в решении математических и экономических задач.
Рассмотрим задачу.
Задача. Аркадий, Борис, Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?
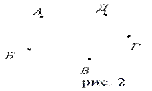
Рис. 2. Нулевой граф с пятью вершинами
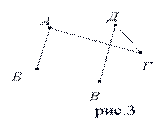
Рис. 3. Неполный граф с пятью вершинами
Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени (рис.2), а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена (рис. 3).
Точки А, Б, В, Г, Д называются вершинами графа, а отрезки линий, соединяющие эти точки — ребрами графа. При изображении графов на рисунках или схемах отрезки могут быть прямолинейными или криволинейными; длины отрезков и расположение точек произвольны.
Например, все три фигуры на рис. 4 изображают один и тот же граф.
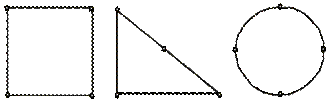
Рис. 4. Графы
Рассмотрим процесс соединения точек А, Б, В, Г, Д ребрами.
1. Ситуация, соответствующая моменту, когда рукопожатия еще не совершались, представляет собой точечную схему, изображенную на рис. 2. Такая схема, состоящая из «изолированных» вершин, называется нулевым графом.
2. Ситуация, когда совершены еще не все рукопожатия, может схематически быть изображена, например, с помощью рис. 3: пожали руки А и Б, А и Г, Д и Г, В и Д. Графы, в которых не построены все возможные ребра, называются неполными графами.
3. На рис. 5 изображен граф, соответствующий всем совершенным рукопожатиям. Этот граф является полным графом.
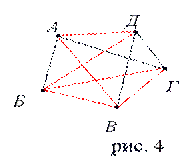
Рис. 5. Полный граф с пятью вершинами
Если подсчитать число ребер графа, изображенного на рисунке, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.
Заметим, что если полный граф имеет n вершин, то количество ребер будет равно n(n-1)/2.
На рисунке 4 ребра превращающие граф в полный граф изображены другим цветом, совокупность вершин графа с этими ребрами называется дополнением графа.
Степень вершины – количество ребер графа, исходящих из этой вершины.
На рис. 3 изображен граф с пятью вершинами. Степень вершины А обозначим Ст.А. На рис. 4: Ст.А = 2, Ст.Б = 1, Ст.В = 1, Ст.Г = 2, Ст.Д = 2.
Вершина называется нечетной ‒ если степень этой вершины нечетная, четной ‒ если степень этой вершины четная.
Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный.
Введем понятие ориентированного графа. В таком графе дуги имеют стрелки, направленные от одной вершины к другой (рис. 6).
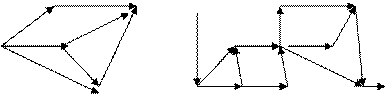
Рис.6. Примеры ориентированных графов
Ориентированный граф был бы полезен, например, для иллюстрации организации перевозок в транспортной задаче. В экономике дугам ориентированного или обычного графа часто приписывают числа, например, стоимость проезда или перевозки груза из пункта А (начальная вершина дуги) в пункт Б (конечная вершина дуги)
Путем в графе от одной вершины к другой называется такая последовательность ребер, по которой можно проложить маршрут между этими вершинами, при этом никакое ребро маршрута не должно встречаться более одного раза. Вершина, от которой проложен маршрут, называется началом пути, вершина в конце маршрута — конец пути. Простой путь – путь, в котором ни одна дуга не встречается дважды. Элементарный путь – путь, в котором ни одна вершина не встречается дважды. Контур – путь, у которого конечная вершина совпадает с начальной вершиной. Длиной пути (контура) называется число дуг пути (или сумма длин его дуг, если последние заданы).
Циклом называется путь, в котором совпадают начало с концом. Если все вершины цикла разные, то такой цикл называется элементарным (или простым) циклом. Если же цикл включает в себя все ребра графа по одному разу, то такой цикл называется Эйлеровой линией. На рис. 7 приведены примеры Эйлеровых линий.
Рис. 7. Примеры Эйлеровой линии
Элементарный путь (контур), проходящий через все вершины графа, называется гамильтоновым путем (контуром).
Две вершины графа называются связными, если в графе существует путь с концами в этих вершинах. Если такого пути не существует, вершины называются не связными.
Так, на рис. 8 любая пара вершин, взятая из набора А, Б, В, Г, Д, будет связной, т.к. от любой из них к любой можно " пройти" по ребрам графа. Пары вершин, одна из которых взята из набора А, Б, В, Г, Д, а другая из набора Е, Ж, З, не будут связными, т.к. от одной к другой " пройти" по ребрам не удается.
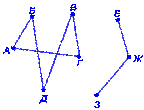
Рис. 8. Примеры связных и несвязных графов
Граф называется связным, если любая пара его вершин — связная.
Граф называется несвязным, если в нем есть хотя бы одна несвязная пара вершин.
На рис.8, очевидно, изображен несвязный граф. Если, например, на рис. 8 между вершинами Д и Е провести ребро, то граф станет связным. Такое ребро в теории графов, после удаления которого, граф из связного превращается в несвязный, называется мостом.
Примерами мостов на рис. 8 могли бы служить ребра ДЕ, AЗ, ВЖ и др., каждое из которых соединяло бы вершины «изолированных» частей графа.
Деревом называется любой связный граф, не имеющий циклов. Договорились считать «деревом» и всякий граф, состоящий из одной (изолированной) вершины.
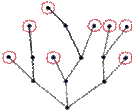
Рис. 9. Дерево
На рисунке приведен пример графа «дерева». Вершина дерева, имеющая степень единицу, называется висячей вершиной (на рис. 9 они отмечены кружком).
Рассмотрим несколько типичных задач принятия решений, связанных с оптимизацией на графах:
1. Задача о кратчайшем пути.
2. Задача о максимальном потоке.
3. Задача коммивояжера.
10.2 Задача о кратчайшем пути
Как кратчайшим путем попасть из одной вершины графа в другую (следовательно, с наименьшим расходом топлива и времени, наиболее дешево попасть из пункта А в пункт Б)? Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число – время движения по этой дуге от начальной вершины до конечной (рис. 10).
Рис. 10. Исходные данные
Ситуацию можно описать не только ориентированным графом с весами, приписанными дугам, но и таблицей (табл. 1).
Табл. 1. Исходные данные к задаче о кратчайшем пути
| Начало дуги | Конец дуги | Время в пути |
Спрашивается: как кратчайшим путем попасть из вершины 1 в вершину 4?
Решение. Введем обозначение: С(Т) ‒ длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) Рассматриваемая задача состоит в вычислении С(4) и указании пути, на котором этот минимум достигается.
Для исходных данных, представленных на рис. 10 и в табл. 1, в вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, поэтому С(3) = 1. Кроме того, очевидно, что С(1) = 0.
В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 4, либо из вершины 5, пройдя путь, равный 5. Поэтому справедливо соотношение
С(4) = min {С(2) + 4; С(5) + 5}.
Таким образом, проведена реструктуризация задачи ‒ нахождение С(4) сведено к нахождению С(2) и С(5).
В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3. Поэтому справедливо соотношение
С(5) = min {С(3) + 2; С(6) + 3}.
Мы знаем, что С(3) = 1. Поэтому
С(5) = min {3; С(6) + 3}.
Поскольку очевидно, что С(6) ‒ положительное число, то из последнего соотношения вытекает, что С(5) = 3.
В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 7, либо из вершины 3, пройдя путь, равный 5, либо из вершины 5, пройдя путь, равный 2. Поэтому справедливо соотношение
С(2) = min {С(1) + 7; С(3) + 5; С(5) + 2}.
Нам известно, что С(1) = 0, С(3) = 1, С(5) = 3. Поэтому
С(2) = min {0 + 7; 1 + 5; 3 + 2} = 5.
Теперь мы можем найти С(4):
С(4) = min {С(2) + 4; С(5) + 5} = min {5 + 4; 3 + 5} = 8.
Таким образом, длина кратчайшего пути равна 8. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 5. Возвращаясь к вычислению С(5), видим, что в вершину 5 надо идти через вершину 3. А в вершину 3 можно попасть только из вершины 1. Итак, кратчайший путь таков:
1 → 3 → 5 → 4.
Задача о кратчайшем пути для конкретных исходных данных (рис.10 и табл. 1) полностью решена.
10.3 Задача о максимальном потоке
По каким маршрутам послать максимально возможное количество грузов из начального пункта в конечный, если пропускная способность путей между пунктами ограничена?
Для решения этой задачи каждой дуге ориентированного графа, соответствующего транспортной системе, должно быть сопоставлено число – пропускная способность этой дуги (рис. 11).
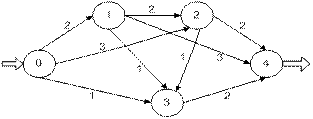
Рис. 11. Исходные данные
Исходные данные о транспортной системе, например, внутризаводской, приведенные на рис.11, можно также задать таблицей (табл. 2).
Табл. 2. Исходные данные к задаче о максимальном потоке
| Пункт отправления | Пункт назначения | Пропускная способность |
Решение задачи о максимальном потоке может быть получено из следующих соображений.
Очевидно, максимальная пропускная способность транспортной системы не превышает 6, поскольку не более 6 единиц грузов можно направить из начального пункта 0, а именно, 2 единицы в пункт 1, 3 единицы в пункт 2 и 1 единицу в пункт 3.
Далее надо добиться, чтобы все 6 вышедших из пункта 0 единиц груза достигли конечного пункта 4. Очевидно, 2 единицы груза, пришедшие в пункт 1, можно непосредственно направить в пункт 4. Пришедшие в пункт 2 грузы придется разделить: 2 единицы сразу направить в пункт 4, а 1 единицу ‒ в промежуточный пункт 3 (из-за ограниченной пропускной способности участка между пунктами 2 и 4). В пункт 3 доставлены такие грузы: 1 единица из пункта 0 и 1 единица из пункта 3. Их направляем в пункт 4.
Итак, максимальная пропускная способность рассматриваемой транспортной системы ‒ 6 единиц груза. При этом не используются внутренние участки (ветки) между пунктами 1 и 2, а также между пунктами 1 и 3. Не догружена ветка между пунктами 1 и 4 ‒ по ней направлены 2 единицы груза при пропускной способности в 3 единицы.
Решение можно представить в виде таблицы (табл. 2) или графа (рис. 12).
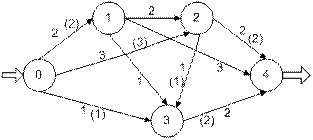
Рис. 12. Решение задачи (числа в скобках)
Табл. 3. Решение задачи о максимальном потоке
| Пункт отправления | Пункт назначения | Пропускная способность | План перевозок |
Дадим формулировку задачи о максимальном потоке в терминах линейного программирования. Пусть ХKM ‒ объем перевозок из пункта К в пункт М. Согласно рис. 11 К = 0, 1, 2, 3, М = 1, 2, 3, 4, причем перевозки возможны лишь в пункт с большим номером. Значит, всего имеется 9 переменных ХKM, а именно, Х 01, Х 02, Х 03, Х 12, Х 13, Х 14, Х 23, Х 24, Х 34. Задача линейного программирования, нацеленная на максимизацию потока, имеет вид:
F → max,
Х01 + Х02 + Х03 = F (0)
- Х01 + Х12 + Х13 + Х14 = 0 (1)
- Х02 ‒ Х12 + Х23 + Х24 = 0 (2)
- Х03 ‒ Х13 ‒ Х23 + Х34 = 0 (3)
- Х14 ‒ Х24 ‒ Х34 = ‒ F (4)
Х01 ≤ 2
Х02 ≤ 3
Х03 ≤ 1
Х12 ≤ 4
Х13 ≤ 1
Х14 ≤ 3
Х23 ≤ 1
Х24 ≤ 2
Х34 ≤ 2
ХКМ ≥ 0, К, М = 0, 1, 2, 3, 4
F ≥ 0.
Здесь F ‒ целевая функция, условие (0) описывает вхождение грузов в транспортную систему. Условия (1) ‒ (3) задают балансовые соотношения для узлов 1- 3 системы. Другими словами, для каждого из внутренних узлов входящий поток грузов равен выходящему потоку, грузы не скапливаются внутри и системы и не " рождаются" в ней. Условие (4) ‒ это условие " выхода" грузов из системы. Вместе с условием (0) оно составляет балансовое соотношение для системы в целом (" вход" равен " выходу"). Следующие девять неравенств задают ограничения на пропускную способность отдельных " веток" транспортной системы. Затем указана неотрицательность объемов перевозок и целевой функции. Ясно, что последнее неравенство вытекает из вида целевой функции (соотношения (0) или (4)) и неотрицательности объемов перевозок. Однако последнее неравенство несет некоторую общую информацию ‒ через систему может быть пропущен либо положительный объем грузов, либо нулевой (например, если внутри системы происходит движение по кругу), но не отрицательный (он не имеет экономического смысла, но формальная математическая модель об этом " не знает").
Литература:
1. Белов В.В. Теория графов / В.В. Белов, Е.М. Воробьев, В.Е. Шаталов. ‒ М.: Высшая школа, 1976. ‒ 392 с.
2/ Электронный учебник по решению задач на графах Татарского института содействия бизнесу. URL: https://www.tisbi.ru/resource/lib/graph/cont.htm
Лекция 11. Основные положения теории планирования экспериментов
11.1 Поверхность отклика
Планирование эксперимента позволяет оптимизировать трудовые, временные и материальные затраты на проведение исследований, обеспечить их наиболее эффективное выполнение, а отсутствие соответствующего плана может существенно повысить трудоемкость исследований или сделать экспериментальную программу полностью безрезультатной.
Исторически теория планирования эксперимента начала развиваться с факторного планирования, основы которого зародились еще в 30-х годах XX столетия. Основы этой теории состоят в построении экономичных планов, по результатам экспериментальных измерений в точках которых можно делать статистические выводы о неизвестных параметрах функций регрессии, причем делать это на основе четко формализованных процедур. Факторное планирование включает построение полных и дробных факторных планов, ортогональных латинских квадратов и сбалансированных блок-схем. В отличие от классического эксперимента, в котором влияние различных значений входных переменных на результаты исследования рассматривается по одному при факторном планировании эти значения одновременно комбинируются в разных вариантах. Это позволяет дать более точные оценки неизвестных параметров регрессии при равном числе измерений.
К настоящему времени сложилась стройная теория планирования эксперимента, оперирующая с достаточно сложным математическим аппаратом, имеющая свою терминологию. Здесь мы рассмотрим лишь основные положения этой теории, позволяющие организовать процесс моделирования не очень сложных систем. При этом мы ограничимся рассмотрением двухуровневых планов, в которых влияние на результат эксперимента каждой из входных переменных изучается на двух уровнях, т.е. при наименьшем и наибольшем значениях этой переменной в пределах исследуемой области. Двухуровневые планы в силу ряда преимуществ получили наибольшее распространение при факторном планировании эксперимента.
Поскольку математические методы планирования эксперимента основаны на кибернетическом подходе, наиболее подходящей моделью эксперимента является «черный ящик», для которого известно лишь то, что подается на его вход, и то, что получается на выходе, а устройство этого ящика значения не имеет. Соответственно мы будем иметь два типа переменных (входных и выходных), которые называют факторами и откликами. Для выяснения различий между ними рассмотрим простой эксперимент, в котором рассматриваются лишь две переменные x и y и целью которого является ответ на вопрос: как при изменении x будет изменяться у В этом случае x – фактор, а у – отклик. В литературе встречаются другие термины: для фактора – режим, независимая переменная, входная переменная, экзогенная переменная; для отклика – реакция, выход, зависимая переменная, переменная состояния, эндогенная переменная. Подобная терминология возникла в связи с тем, что первые исследования с применением статистических экспериментов проводились в сельском хозяйстве, биологии, а затем стремительно вторгались в другие ниши, пополняясь там терминами, наиболее близкими и понятными читателям.
Каждый фактор xi может принимать в эксперименте одно из нескольких значений, называемых уровнями. Каждому уровню соответствует определенная точка в многомерном пространстве, а множество таких точек образует поверхность отклика. На рис. 1 показана поверхность отклика для двухфакторного эксперимента. Факторами являются переменные х1 и х2. В точках 1, 2, 3, 4 эти факторы принимают определенные значения, которым отвечают соответствующие точки на поверхности отклика.
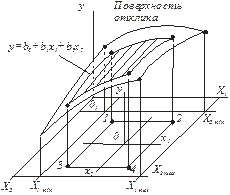
Рис. 1.Поверхность отклика
Конфигурация поверхности отклика, следовательно, функция не известна. Целью
(1)
эксперимента является либо описание этой поверхности (хотя бы приближенное) в интересной для исследователя области варьирования факторов, либо определение экстремального значения отклика. Вторая задача может быть сведена к пошаговому выполнению первой, поэтому на начальном этапе нас будет интересовать только поиск аналитического выражения, близкого к искомой функции (1) в заданной области. Этот поиск осуществляют на основе обработки экспериментальных данных в точках 1, 2, 3, 4 (рис. 3.3) факторного пространства.
11.2 Этапы планирования эксперимента
Общая схема планирования экспериментов для решения экстремальных задач состоит из следующих этапов:
1) постановка задачи;
2) выбор параметра оптимизации;
3) выбор факторов;
4) составление линейного плана;
5) реализация линейного плана и построение линейной модели;
6) поиск области экстремума;
7) описание области экстремума;
8) интерпретация результатов.
Постановка задачи. Решение любой задачи начинается с ее формулировки. При этом необходимо иметь ясное, четкое и вполне однозначное представление о цели работы. Желательно, чтобы эта цель была сформулирована количественно, так как планирование экспериментов связано прежде всего с установлением количественных связей между входными и выходными параметрами изучаемой системы. Разумеется, объект обследования должен быть управляемым.
Выбор параметра оптимизации. Одним из наиболее ответственных этапов является выбор параметра оптимизации. Он должен быть однозначным, характеризоваться числами, действительно определять оптимум. Надо стремиться к тому, чтобы параметр был только один, имел ясный физический смысл и оценивался с максимальной статистической эффективностью (последнее позволяет сократить до минимума число параллельных опытов).
Простейший случай имеет место, когда заранее известен и сам параметр, и то его значение, к которому следует стремиться. При этом иногда приходится изменять вид параметра (например, переходить от его натуральных значений к логарифмам, обратным величинам и пр.). Если значение параметра, к которому следует стремиться, неизвестно, все же следует пытаться установить ограничения его величины хотя бы с одной стороны.
Иногда параметр оптимизации приходится изменять из-за технических трудностей, связанных, например, с отсутствием необходимых методик или достоверных методов оценки. В этих условиях можно применять параметры, дающие косвенные оценки, но поиск экстремума становится во многом интуитивным, а интерпретация результатов усложняется.
Часто возникают трудности в количественной оценке параметра оптимизации. Тогда можно использовать субъективные ранговые параметры, такие, как сорт, балл, класс и др. Некоторые методы планирования экспериментов вообще не требуют количественных оценок параметра оптимизации.
Выбор факторов. Не менее сложен этап выбора факторов, влияющих на изменение параметра оптимизации. Если при постановке задачи пропустить какой-нибудь сильно влияющий фактор, то вся работа окажется бесполезной. Поэтому при планировании экспериментов необходимо включать в план исследования все факторы, которые могут влиять на параметр оптимизации. Часто выбранных факторов оказывается очень много; если число их превышает 10, то возникает задача отсеивания незначимых факторов.
Факторы, которые по тем или иным причинам невозможно учесть в эксперименте, необходимо в течение всех опытов стабилизировать на постоянных уровнях.
Важным требованием, предъявляемым к факторам, является невозможность их взаимозаменяемости. Взаимозаменяемость не следует допускать даже для двух любых факторов из общей совокупности.
Выбирая факторы, рекомендуется учитывать область, ограничивающую их возможное варьирование. Желательно, чтобы факторы имели количественную оценку, хотя планирование экспериментов возможно, когда некоторые факторы представлены качественно.
После выбора факторов для каждого из них устанавливают основной уровень и интервалы варьирования. Последние следует выбирать таким образом, чтобы их величина не превышала удвоенной среднеквадратичной ошибки в определении данного фактора.
Составление линейного плана и определение коэффициентов регрессии производят по правилам, изложенным в первых двух разделах данной главы.
Определение доверительных интервалов коэффициентов регрессии. Если проводятся повторные серии опытов или осуществляется несколько прогонов модели на компьютере, то возникает задача статистической оценки коэффициентов регрессии. После определения таких коэффициентов следует прежде всего установить их статистическую значимость. С этой целью проверяют гипотезу об однородности выборочных дисперсий и вычисляют доверительные интервалы коэффициентов регрессии.
Статистический анализ уравнения регрессии. После вычисления коэффициентов регрессии и проверки их значимости проводят статистический анализ уравнения регрессии. С этой целью проверяют гипотезу об адекватности данного уравнения, т. е. ищут ответ на вопрос, соответствует ли полученное линейное уравнение изучаемому явлению или необходима более сложная модель.
Количественной оценкой адекватности уравнения регрессии является дисперсия неадекватности, характеризующая квадрат отклонений экспериментальных значений у от теоретических. Гипотезу адекватности обычно проверяют с помощью критерия Фишера, но возможно использование других критериев.
Адекватность линейного уравнения можно проверить и другим способом. Свободный член уравнения регрессии bо является, по сути дела, оценкой результата опыта на основном уровне, когда все остальные факторы исключены. Поэтому, сделав соответствующий опыт, можно сравнить его результат с величиной свободного члена, т.е. проверить гипотезу о равенстве нулю суммы коэффициентов при квадратичных членах (нуль-гипотезу). Нуль-гипотеза может быть принята, если разность | b 0— у0 | не превышает среднеквадратической ошибки эксперимента. Значимость этого различия иногда проверяют сопоставлением с критерием Стьюдента.
Выбор факторов. При проведении эксперимента факторы могут быть управляемыми и неуправляемыми, наблюдаемыми и ненаблюдаемыми, изучаемыми и неизучаемыми, количественными и качественными, фиксированными и случайными.
Фактор является управляемым, если его уровни назначаются лицом, проводящим эксперимент, в соответствии с задачами исследования. В процессе эксперимента все управляемые факторы должны поддерживаться на заданном уровне или изменяться в соответствии с заданной программой.
Не всяким наблюдаемым (т.е. фиксируемым в процессе эксперимента) фактором можно управлять. Такие наблюдаемые, но не управляемые факторы получили название сопутствующих. К ним относятся, в частности, воздействия внешней среды. Обычно сопутствующих факторов бывает довольно много, поэтому рационально учитывать влияние лишь тех из них, которые наиболее существенно воздействуют на результаты эксперимента.
После выбора факторов для каждого из них следует определить область, ограничивающую их возможное варьирование, и назначить основной уровень. Если, например, по условиям эксперимента нас интересует диапазон температуры воды от 20 до 60°С, то основной уровень (для середины интервала) составит 40°, нижний уровень 20°, верхний уровень 60°С. Разница значений между верхним и нижним уровнями фактора не может быть больше физически возможной. Например, для температуры обычной воды при нормальных условиях эта разность не может превысить 100°С. При этом интервал варьирования не должен быть меньше ошибки фиксирования уровня фактора, иначе верхний и нижний уровни окажутся Факторы, которые по тем или иным причинам невозможно учесть в эксперименте, необходимо во всех опытах стабилизировать на постоянных уровнях.
11.3 Обработка и анализ результатов моделирования
Для обработки данных эксперимента существуют различные методы, зависящие от целей исследования и вида получаемых при моделировании характеристик.
В результате эксперимента получают набор данных, между которыми может существовать или отсутствовать функциональная либо структурная связь. Если такая связь между факторами и откликом существует, то она проявляется в эксперименте в неявном виде, а для использования результатов эксперимента в практических целях неявную зависимость следует сделать явной и представить ее в виде функции, системы уравнений, номограммы, графика и т. п. Если функциональная зависимость между факторами и откликом не существует, то следует обработать их независимо друг от друга по правилам математической статистики.
Первым шагом при записи аналитического выражения, аппроксимирующего требуемую зависимость, является нанесение экспериментальных точек на график в прямоугольной системе координат, В результате будет получена диаграмма разброса (рис. 2), из которой часто удается визуально найти плавную кривую и определить соответствующую ей функциональную зависимость. Точки, изображенные на рис. 3.6, а, группируются около прямой, а точки, показанные на схеме б, соответствуют кривой. Описание точек схемы в зависит от задач эксперимента: это может быть прямая линия или некоторая периодическая функция. При построении диаграммы разброса нужно иметь в виду постоянно возникающую трудность графического изображения соотношений, связывающих большое число переменных. Частично эту трудность можно преодолеть, построив несколько графиков, каждый из которых отражает зависимость функции отклика от одной переменной при фиксированных значениях всех остальных.
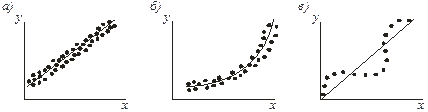
Рис. 2.Диаграммы разброса
Задачу подбора вида функции, наилучшим образом соответствующей конфигурации кривой, называют подгонкой кривых по точкам. Для этой цели используют графические изображения наиболее характерных функций, некоторые из которых показаны на рис. 3.
ри подгонке кривых по точкам прежде всего следует определить количественный принцип соответствия теоретической функции экспериментальным точкам. В качестве меры такого соответствия было бы логичным принять минимальные отклонения по всем точкам, т. е. суммы всех отклонений. Но поскольку отклонения теоретических значений от экспериментальных могут быть положительными и отрицательными, то с математической точки зрения проще предварительно возвести эти отклонения в квадрат и обеспечить минимум для суммы квадратов отклонений. Этот метод, названный методом наименьших квадратов, соответствует критерию наилучшего приближения.
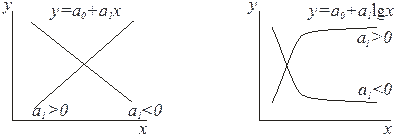
а)
б)
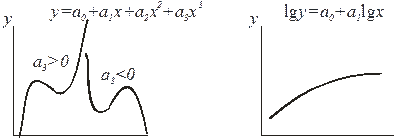
в)
Рис. 3. Различные виды регрессионных кривых
Для поиска математических зависимостей между переменнымипо накопленным экспериментальным данным обычно используют методы регрессионного и корреляционного анализов. Регрессионный анализ дает возможность построить по экспериментальным данным уравнение, а корреляционный анализ позволяет судить, насколько хорошо экспериментальные точки согласуются с выбранным уравнением, а также насколько тесна связь между двумя и более величинами, наблюдаемыми ификсируемыми при моделировании.
Регрессионный анализ. Математический метод, обеспечивающий такую подгонку выбранной кривой, при которой экспериментальные точки описывают ее наилучшим образом в смысле критерия наименьших квадратов, называют регрессионным анализом.
Корреляционный анализ. Наилучшее приближение теоретической кривой к экспериментальным данным еще не означает, что реально существующая физическая зависимость соответствует именно этой кривой. Наглядный этому пример дает рис. 3, в. Описание экспериментальных точек прямой линией вполне соответствует методу наименьших квадратов, но не соответствует физической сущности явления, если мы не постулируем приближенное представление последнего в линейной постановке.
Для оценки согласованности экспериментальных точек с теоретическими прогнозами используют понятие корреляции. Если регрессия определяет эту согласованность по форме, то корреляция показывает, насколько точно она отражает действительность. Вместе с тем корреляция между переменными означает лишь то, что их изменения взаимосвязаны, однако это еще не доказывает наличие причинно-следственной связи между переменными.
Мерой корреляционной связи между переменными X a Y служит коэффициент корреляции rху, представляющий собой отношение корреляционного момента (математического ожидания произведения отклонений X и Y) к произведению средних квадратических отклонений этих величин
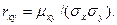
Для случая простой линейной регрессионной задачи (т.е. для случая, когда имеются одна зависимая и одна независимая переменные, связанные между собой линейно) коэффициент корреляции вычисляют по формуле
(2)
Коэффициент корреляции лежит в пределах от -1 до +1. Коэффициент корреляции, равный нулю, соответствует полному отсутствию корреляции (рис. 4, а). При наличии слабой (схема б) или сильной (схема в) положительной корреляции коэффициент корреляции соответственно равен +1 или близок к нему. Если этот коэффициент равен ‒ 1, то имеет место сильная отрицательная корреляция (схема г).
Рис. 4. Виды корреляции
Литература:
1. Ильина Н.В. Системный анализ и моделирование процессов в техносфере: Учеб. пособие / Н.В. Ильина, Д.Д. Лапшин, В.И. Федянин. – Ч. 1. Воронеж: ГОУВПО «Воронежский государственный технический университет, 2008. – 206 с.
|
|