Перспективные изображения

Следует заметить, что реально существующий мир и видимый нами

мир – не одно и то же. Например: рельсы железной дороги кажутся нам сходящимися на горизонте, хотя мы прекрасно знаем, что это не так. В сочинении Евклида присутствует постулат, повествующий о том, что мы воспринимаем предметы, когда исходящие от них прямолинейные лучи света сходятся в нашем глазу. Таким образом, всю систему лучей зрения можно представить в виде " пирамиды зрения", вершина которой находится в глазу наблюдателя, а основанием служит рассматриваемый объект.

Перспектива была не просто объективным геометрическим методом построения изображений, но и " физиологическим" методом, т.е. методом, учитывающим закономерности работы человеческого глаза. Именно поэтому перспектива давала изображения столь реалистичные – " похожие" на видимую глазом натуру.

Перспектива открыла возможности, позволяющие, используя геомет-

рический метод, строить изображения не отдельного предмета, а всего видимого трехмерного пространства, всего окружающего мира, чего в аксонометрии просто невозможно.

В основу современной теории перспективы положен метод построения перспективного изображения на плоской прозрачной картине (плоскости). Наглядно этот процесс можно представить следующим образом.

Наблюдатель стоит перед окном и, не изменяя положения своего тела и головы, обводит на стекле все то, что видит за окном в пределах его рамы.

Полученное на стекле изображение и будет перспективным изображением предметов, видимых за окном.

Изучение закономерностей построений перспективных изображений

удобнее рассматривать на так называемом перспективном аппарате

(рис. 25).

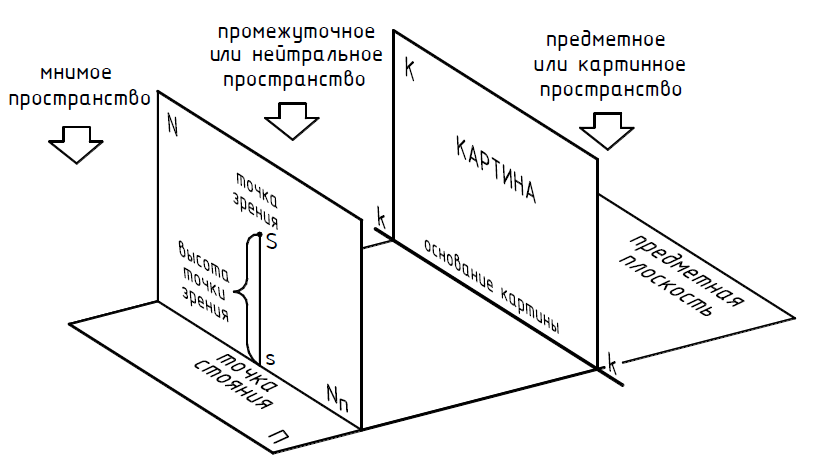
Рис. 25. Перспективный аппарат

Предметная плоскость П располагается горизонтально и подразуме-

вается безграничной. На ней находятся картина, наблюдатель и изображаемые объекты.

Картинная плоскость К – это вертикальная плоскость, перпендику-

лярная к предметной плоскости. На ней строятся перспективное изображение.

Основание картины кк – линия пересечения картинной плоскости с

предметной.

Точка зрения S – это центр проецирования, через который проходят

проецирующие лучи ко всем точкам изображаемого предмета. Точка зрения условно определяет положение " глаз" наблюдателя.

Точка стояния s – основание перпендикуляра, проведенного из точки

зрения на предметную плоскость.

Высота точки зрения Ss – длина перпендикуляра, определяющего

расстояние от точки зрения до предметной плоскости. Чаще всего высоту точки зрения принимают равной среднему значению роста человека.

Нейтральная плоскость N – плоскость зрителя, проходящая через

высоту точки зрения параллельно картинной плоскости.

Перспективное изображение объекта и степень его соответствия зри-

тельному восприятию и пространственному образу во многом зависит от выбора элементов перспективного аппарата: предметной, картинной плоскостей и точки зрения, которые взаимосвязаны с картиной. На основе этой взаимосвязи определяются основные (или главные) элементы картины (рис. 26): форма и размер рамки с ее основанием kk; линия горизонта hh,

определяющая высоту точки зрения; главная точка Р, показывающая точку непосредственно перед наблюдателем; дистанционные точки D1 и D2, расположенные на линии горизонта по обе стороны от главной точки на расстоянии, равном расстоянию от наблюдателя до картины.

Рис. 26. Элементы картинной плоскости

Элементы картины дизайнер (проектировщик, художник) выбирает в

зависимости от назначения перспективного изображения.

Принципы построения перспективы продемонстрируем на примере

создания перспективного изображения простейшего из геометрических объектов – точки.

При построении перспективы точки необходимо вначале построить ее

основание – ортогональную проекцию на предметную плоскость. Например, для точки A основанием будет точка AП (рис. 27, а).

Итак, для построения перспективы точки в нее (точка A) и в ее осно-

вание (точка AП) из точки зрения S проводят лучи зрения и находят точки (A', A'П) пересечения их с картинной плоскостью. Для этого лучи зрения заключают в вертикальную плоскость и строят линию пересечения ее с картиной (рис. 27, а). Точки пересечения лучей зрения с линией пересечения плоскостей определяют перспективу заданной точки A и ее основания – точки AП.

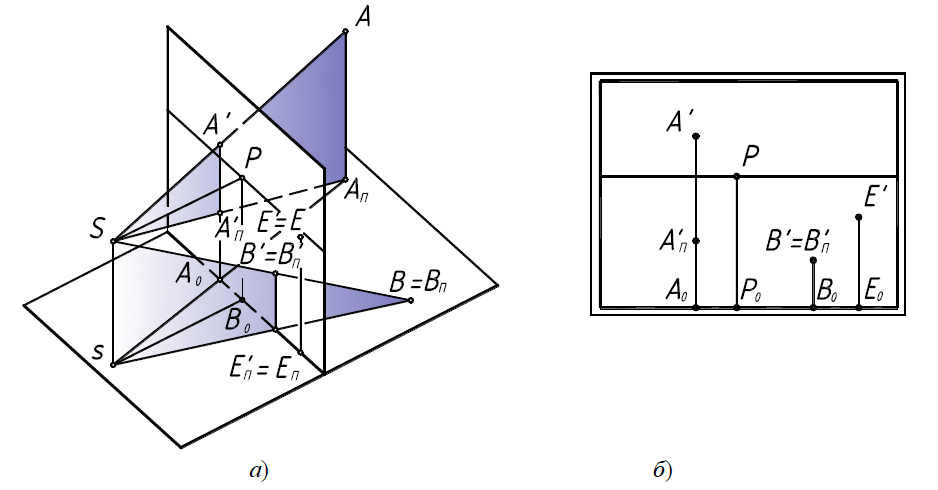
Рис. 27. Перспективное изображение точек

На рисунке 27 также показано построение точки B, которая принад-

лежит предметной плоскости, т.е. совпадает со своим основанием – точкой BП, и точки Е, расположенной в картинной плоскости, а, следовательно, совпадающей со своим перспективным изображением.

Сравнивая пространственное положение точек (рис. 27, а) с их пер-

спективным изображением на картине (рис. 27, б), рассмотрим удаленность каждой из них относительно наблюдателя. На перспективном аппарате видно, что точка B расположена ближе к картинной плоскости, чем точка A. На картине это расположение отражено расстоянием их проекций (А'П и В'П) от основания картины: величина А'ПА0 больше В'ПВ0, следовательно, точка А дальше, а В ближе к картинной плоскости. Из всех трех представленных точек самая ближняя к наблюдателю – это точка Е, так как она находится в плоскости картины, а ее проекция ЕП на предметную плоскость лежит в основании картины.

Кроме удаленности точек по перспективному изображению можно

определить высоту расположения точек относительно предметной плоскости. Так, точка В лежит в предметной плоскости (рис. 27, а) и ее высота равна нулю. Именно поэтому ее перспективное изображение совпадает с перспективным изображением ее основания (рис. 27, б). Точка А отстоит от предметной плоскости на расстоянии ААП, перспективным изображением которого является отрезок А'А'П. Кроме того, по картине можно сказать, что точка А расположена выше линии горизонта, а точки В и Е ниже.

Перспективные изображения геометрических фигур, аналогично их

построению в ортогональных проекциях и в аксонометрии, строятся с помощью опорных (характерных) точек – вершин, которые определяют положение ребер (рис. 28).

Рис. 28. Перспективное изображение многогранников

Перспектива окружности для предметов, имеющих округлые формы,

в зависимости от расположения относительно картины и точки зрения, может иметь различное начертание. Окружность изобразится в виде отрезка, если она принадлежит плоскости, параллельной предметной плоскости и расположенной на уровне линии горизонта, либо в вертикальном расположении непосредственно перед наблюдателем. При расположении окружности в плоскости, параллельной картине, она сохранит свое начертание, то есть изобразится в виде окружности. Во всех остальных случаях

перспективным изображением окружности является эллипс, либо его

часть.

Вспомним, что эллипс – это замкнутая плоская лекальная кривая,

симметричная относительно двух взаимно перпендикулярных осей

(рис. 29, а). Большая АВ и малая CD оси эллипса, пересекаясь в его центре О, делятся пополам, как и любой диаметр, например EL. Кроме того, эллипс имеет сопряженные диаметры, которые являются изображением двух взаимно перпендикулярных диаметров окружности. Диаметр MN является сопряженным, поскольку он проходит через середину хорды, которая параллельна заданному диаметру EL.

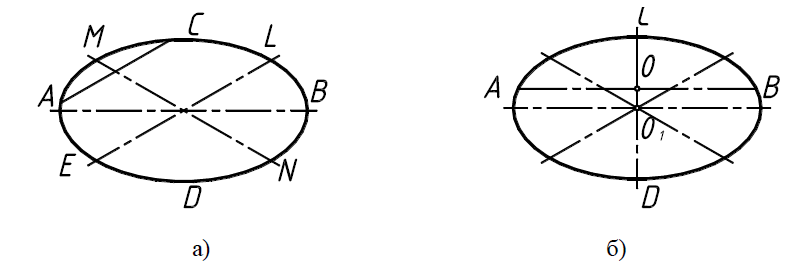
Рис. 29. Свойства эллипса и его перспективное изображение

Эллипсы, являющиеся в перспективе изображением окружности, сохраняет свои свойства. Однако перспективное изображение горизонтального диаметра окружности с центром О не является большой осью эллипса с центром О1, так как по закону перспективы ближняя половина окружности будет больше, чем дальняя (рис. 29, б).

Построение перспективы эллипса, как и другой лекальной кривой,

сводится к построению ряда его точек, которые затем соединяются плавной кривой линией.

Отличия изображений эллипса в перспективе зависит от расположения его относительно горизонта (рис. 30, а) и от смещения относительно главной точки Р (рис. 30, б).

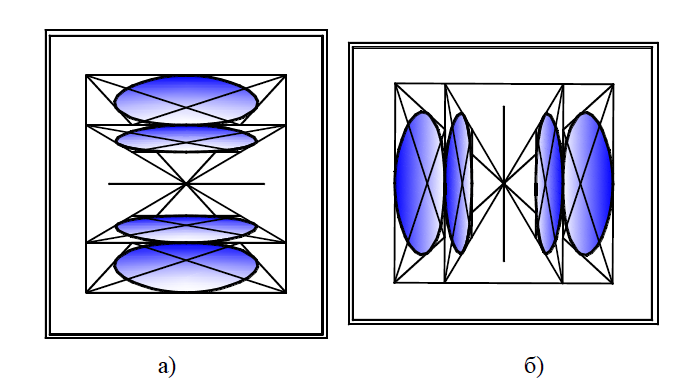
Рис. 30. Перспективные изображения эллипса

Непосредственно само изображение окружности строится с помощью

описанного вокруг нее квадрата. Этот способ является основным и наиболее простым и практически удобным. Сущность способа заключается в том, что сначала во фронтальном расположении под основанием картины строят вспомогательный квадрат KLMN с вписанной окружностью (рис. 31). Затем отмечаются восемь точек: четыре – середины сторон квадрата или же концы сопряженных диаметров окружности (горизонтального и вертикального), и четыре – точки пересечения окружности с диагоналями квадрата.

Для построения перспективного изображения окружности, лежащей в

предметной плоскости, вначале необходимо на картине построить квадрат KLMN, проведя глубинные прямые, сходящиеся на линии горизонта в главной точке Р. Прямая линия, проведенная из точки N в дистанционную точку D на пересечении с глубинной прямой. определит положение дальней горизонтальной стороны LM квадрата. Построение второй диагонали квадрата в пересечении с построенной задаст центр окружности. Через него можно провести два диаметра: вертикальный, уходящий в точку Р, и горизонтальный. Концы построенных диаметров являются четырьмя из восьми искомых точек. Для нахождения еще четырех точек необходимо провести две вспомогательные глубинные прямые, месторасположение которых определяется на построенной вспомогательной окружности (вертикальные прямые 5-6 и 8-7). Соединив последовательно все восемь построенных точек плавной линией, получим перспективное изображение окружности – эллипс.

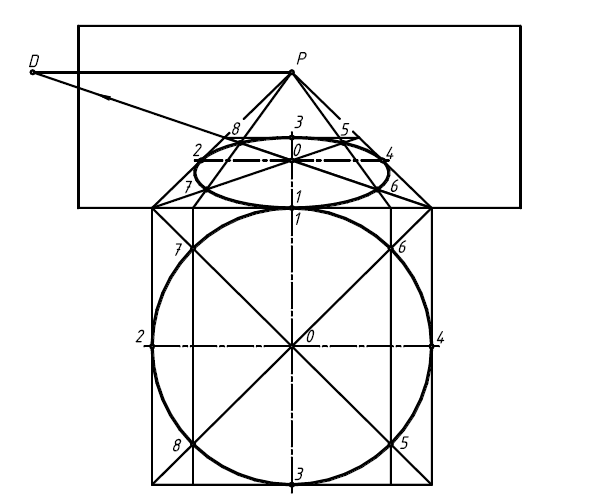
Рис. 31. Перспективное изображение окружности

Построение окружности в перспективе достаточно точно позволяет

изображать предметы, имеющие круглые очертания их формы (рис. 32).

Рис. 32. Перспективное изображение конуса и цилиндра

Применение центрального проецирования в перспективе позволяет

создавать наиболее реалистичные изображения, но ввиду сложности построений и значительных искажений формы и размеров, данный метод получения изображения применяют художники, дизайнеры, архитекторы в архитектурно-строительных проектах.

Что касается аксонометрических проекций, то в них нет перспективных искажений, а для упрощения процесса построения, на их основе был изобретен еще один метод построения изображений – технический рисунок.