Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Комплексный чертеж.

В основе построения комплексного чертежа лежит ортогональное проецирование, которое является частным случаем параллельного проецирования. Слово " ортогональный" (с греческого ortos – прямой, gonia – угол) означает " прямоугольный". То есть направление параллельного проецирования, а, следовательно, и проецирующие лучи перпендикулярны к плоскости проекций (к картине).

Несмотря на то, что ортогональные проекции известны человечеству с незапамятных времен, простая мысль использовать две ортогональные проекции для получения взаимно однозначного отображения пространства на плоскость пришла французскому математику Гаспару Монжу (1746-1818) лишь в конце XVIII в. Простота метода Монжа ошеломила современников.

Суть его метода заключается в следующем: пространственный объект

проецируется ортогонально (т.е. перпендикулярно) на одну плоскость и также проецируется на некоторую другую плоскость, перпендикулярную первой (рис. 10, а). Затем одна из этих плоскостей поворачивается вокруг прямой пересечения этих плоскостей, до их совмещения (рис. 10, б). В результате в одной и той же плоскости оказываются две различные проекции (два изображения) рассматриваемого объекта, по которым уже можно,

методом Монжа, восстановить размеры, углы и т.д., имеющиеся у данного пространственного объекта в натуре. Данное изображение называется комплексным чертежом (рис. 10, в).

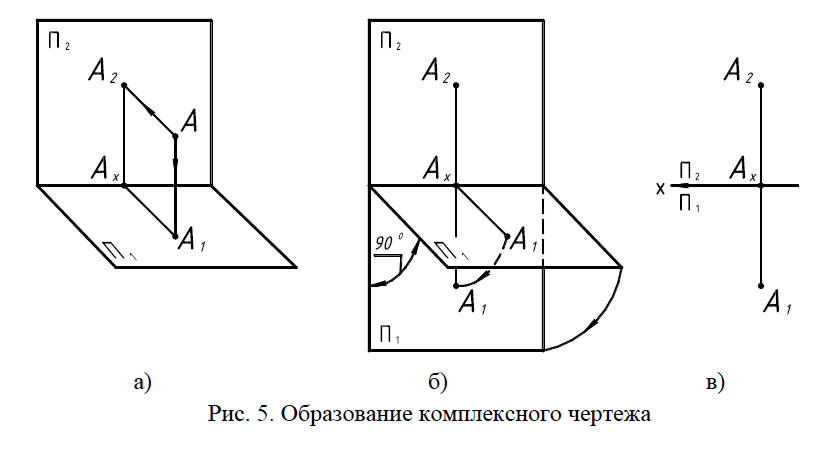
Рис. 10. Образование комплексного чертежа

Построение проекций гранных поверхностей сводится к построению проекций некоторых точек и прямых линий, принадлежащих этой поверхности, например, вершины и ребра (рис. 11). На рисунке 6 показан процесс построения комплексного чертежа четырехгранной призмы (рис. 11, а).

Следует заметить, что ортогональные проекции изображаемого объекта связаны между собой (рис. 11, б), так как он и его положение неизменны относительно ортогональной системы плоскостей проекций.

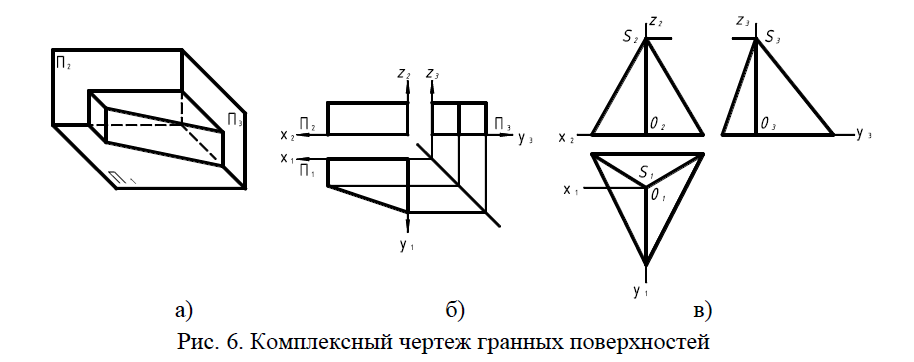
Рис.11. Комплексный чертеж гранных поверхностей

Образование комплексного чертежа осуществляется путем вращения

плоскостей проекций вокруг координатных осей до их совмещении. Положение точки в пространстве определяется тремя координатами: x, y, z.

Их числовые значения определяются расстояниями от точки до плоскостей проекций, которые равны длине перпендикуляров, опущенных из точки на эти плоскости проекций (рис. 12).

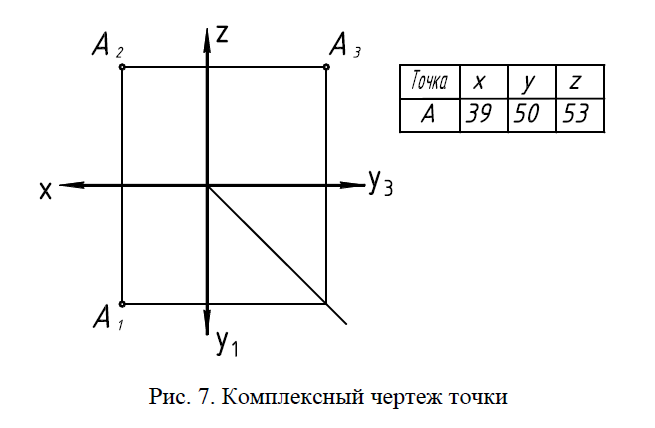
Рис.12. Комплексный чертеж точки

Ортогональное проецирование сохраняет взаимное расположение элементов (точек, прямых, плоскостей), что позволяет решать задачи различного характера, например, построение проекции точки, принадлежащей поверхности пирамиды (рис. 13).

Рис. 13. Комплексный чертеж пирамиды и точки на ее поверхности

Правила изображения изделий, сооружений и их элементов устанавливает ГОСТ 2.305-68. Изображения выполняются по методу прямоугольного проецирования
(в аксонометрии допускается косоугольное проецирование).
При этом предмет располагают между наблюдателем и соответствующей плоскостью проекций. За основные плоскости проекций принимают шесть граней куба. Изображение на фронтальной плоскости (вид спереди) является главным. Изображения разделяются на виды, разрезы, сечения.
Вид - изображение обращенной к наблюдателю видимой части поверхности предмета, который располагают так, чтобы изображение давало наиболее полное представление о форме и размерах предмета.

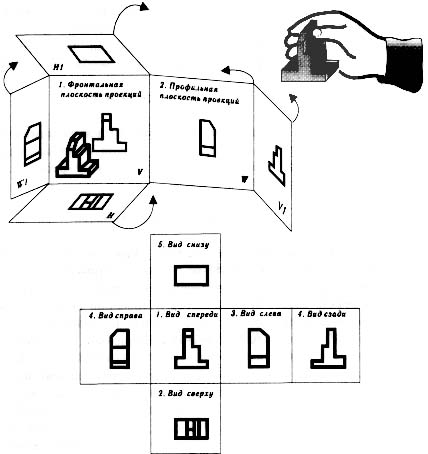
Рис.14. Основные виды

Основные виды: вид спереди (главный вид); вид сверху; вид слева; вид справа; вид снизу; вид сзади. Если часть предмет невозможно показать на основных видах без искажения формы и размеров, то используют дополнительный вид. Изображение отдельного, ограниченного места предмета называется местным видом.