Прямоугольные изометрические проекции геометрических фигур.

В прямоугольной изометрической проекции оси x, y, z расположены под углом 120º друг к другу. При этом ось z всегда располагается вертикально. Все коэффициенты искажения по аксонометрическим осям одинаковы и равны 0, 82, поэтому размеры изображаемого объекта вдоль осей, при создании аксонометрического изображения, должны быть умножены на данный коэффициент искажения. Такая изометрия называется точной или теоретической. Для упрощения обычно применяют приведенную или практическую изометрию, выполненную в масштабе 1, 22: 1. При этом применяют приведенные коэффициенты искажения, которые равны единице по всем трем осям, что очень удобно при выполнении построении.

Процесс построения изометрических изображений " плоских" геомет-

рических фигур начинают с построения их исходного изображения.

Например, для построения изометрии правильного пятиугольника сначала необходимо построить его ортогональную проекцию (рис. 20, а), на кото-

рой можно будет замерять необходимые расстояния: a, k, m, n и отклады-

вать их вдоль направления соответствующих координатных осей (рис. 20, б).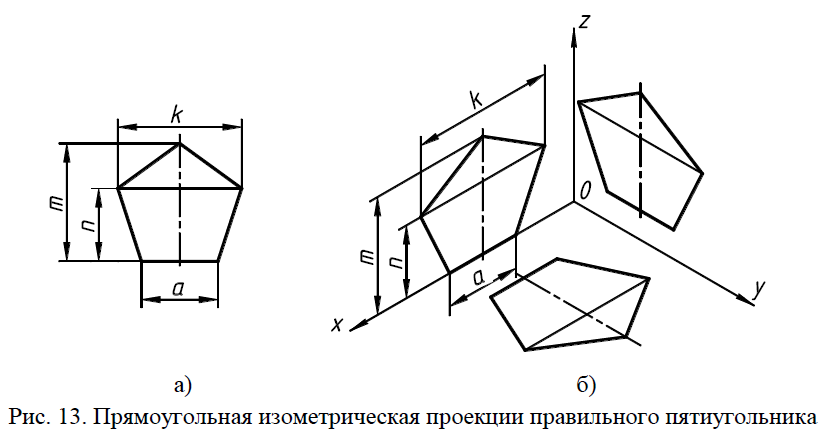

Рис. 20. Прямоугольная изометрическая проекция правильного пятиугольника

На рисунке 19, а) изображена изометрическая проекция куба с

окружностями, вписанными в его грани. Квадратные грани куба будут

изображаться в виде ромбов, а окружности – в виде эллипсов. Стоит заметить, что малая ось каждого эллипса всегда перпендикулярна его большой оси.

В зависимости от того, какой плоскости проекций принадлежит эл-

липс, его малая ось будет располагаться параллельно одной из координационных осей. Так, например, если окружность лежит в плоскости XOY,

то его малая ось будет располагаться параллельно оси z, а большая ось будет ей перпендикулярна (рис. 21, а). Аналогично, если эллипс лежит в плоскости XOZ, то малая ось параллельна оси y, а если эллипс в YOZ, то малая ось сонаправлена с осью x. При этом длина малой оси равна 0, 71d, где d – диаметр изображаемой окружности, а большая ось – 1, 22d (рис. 21, б).

Рис.21. Прямоуголная изометрическая проекция окружности

Построение изометрических проекций геометрических тел, в частно-

сти многогранников, сводится к определению аксонометрических проекций их вершин, которые затем соединяются между собой отрезками прямых линий.

На рисунке 22 показано построение изометрического изображения правильной шестигранной пирамиды, основание которой лежит в плоскости XOY, а высота пирамиды совпадает с осью z, по ее ортогональным проекциям (рис. 22, а).

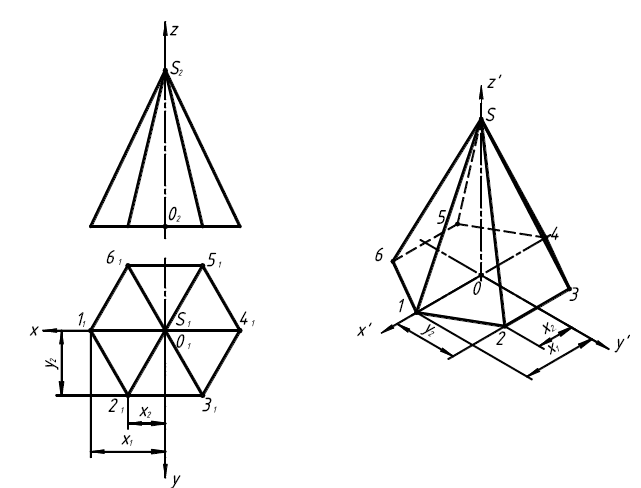
Рис. 22. Прямоугольная изометрия правильной шестиугольной пирамиды

Очень часто для повышения наглядности аксонометрического изоб-

ражения выполняются разрезы изображаемого объекта, то есть предмет изображают с удаленной некоторой ее частью (рис. 23). При этом секущие плоскости располагаются параллельно координатным плоскостям. Для обозначения материала предмета в разрезе наносят штриховку

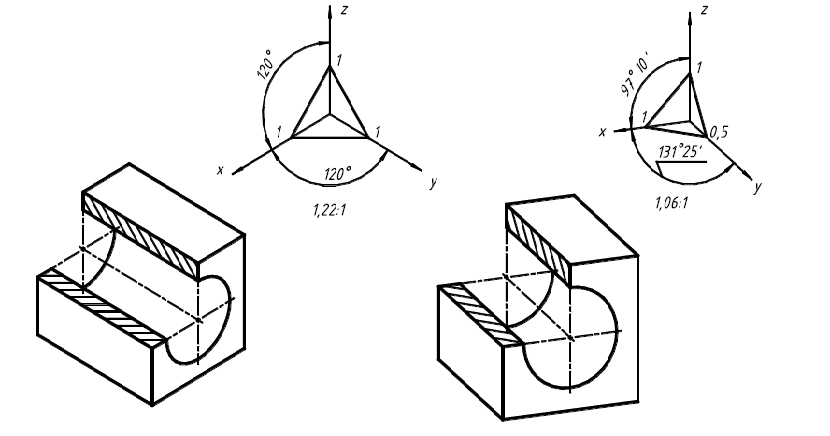
Рис. 23. Аксонометрические проекции детали с четвертью выреза

Линии штриховки наносятся параллельно одной из диагоналей квад-

ратов, лежащих в соответствующих координатных плоскостях (рис. 24).

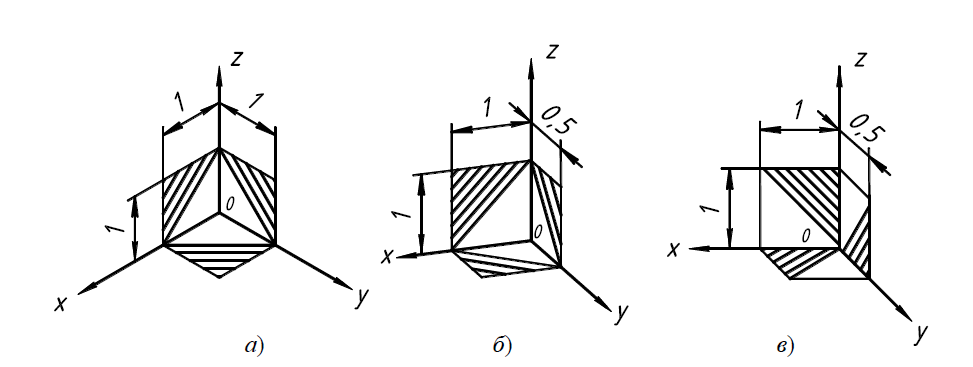
Рис. 24. Штриховка на аксометрических изображениях

а) в прямоугольной изометрии; б) в прямоугольной диметрии;

в) в косоугольной диметрии

Аксонометрические изображения является достаточно наглядными.

Однако перспектива наиболее реалистичнее передает видимый нами объект, так как аппарат центрального проецирования более всего соответствует аппарату человеческого глаза, но перспективные проекции являются и наиболее трудными для построения.