Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Свойства сходящихся последовательностей в некоторых метрических пространствах

Теорема 5.1 (о покоординатной сходимости последовательности в метрическом пространства R^m). Для того, чтобы последовательность точек метрического пространства R^m (х_n = (х₁⁽ⁿ⁾, х₂⁽ⁿ⁾, …, х_m⁽ⁿ⁾, …)) сходилась к точке а = (а₁, а₂, …, а_m) этого пространства, необходимо и достаточно, чтобы числовые последовательности (х₁⁽ⁿ⁾), (х₂⁽ⁿ⁾), …, (х_m⁽ⁿ⁾) сходились соответственно к числам а₁, а₂, …, а_m:

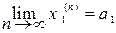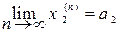, ,..., (5.1)

Если выполняются условия (1), то говорят, что последовательность (х_n)сходится к точке а покоординатно.

3необходимости.

Пусть 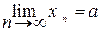(5.2) в метрическом пространстве R^m.

Докажем, что выполняются равенства (5.1).

В силу равенства (5.2) по определению предела последовательности в метрическом пространстве R^m будем иметь:

(" e> 0)($N (e))(" n> N) Þ [r (x_n, а) < e ],

где r - метрика метрического пространства R^m :

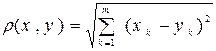" x, yÎ R^m.

Неравенство r (x_n, а) < e примет вид:

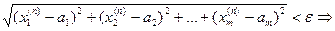
Þ ½ x₁⁽ⁿ⁾-a₁ ½ < e, ½ x₂⁽ⁿ⁾- a₂ ½ < e, …, ½ x_m⁽ⁿ⁾-a_m ½ < e.

Таким образом, если k = 1, 2, …, m доказано, что

(" e> 0)($N (e))(" n> N) Þ [½ x_k⁽ⁿ⁾- a_k ½ < e 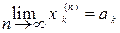]Þ Þ

равенство (5.1). 4

3достаточности.

Пусть имеют место равенства (5.1).

Докажем, что 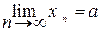(5.2) в метрическом пространстве R^m.

Пусть e - произвольное положительное число, в частности пусть его роль играет число .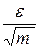

Поэтому (" e> 0)($n_k)(" n> n_k) Þ ½ x_k⁽ⁿ⁾-a_k ½ < 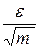, k = 1, 2, …, m.

Выберем число N = max { n₁, n₂, …, n_m }. Тогда " n> N Þ

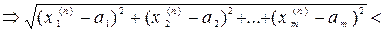
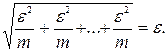
Мы доказали, что(" e> 0)($N (e))(" n> N) Þ [ r (x_n, а) < e ]Þ 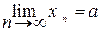.4

Пример 5.1. Найти предел a = (a₁, a₂)

последовательности в пространстве R².

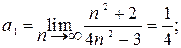
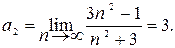
Таким образом, 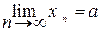= (1/4; 3).

Теорема 5.2 (Больцано-Вейерштрасса). Из всякой ограниченной последовательности пространства R^m можно выделить сходящуюся подпоследовательность.

Частный случай этой теоремы для пространства R¹ был доказан на первом курсе.

Теорема 5.3. Для того, чтобы последовательность (x_n) точек метрического пространства С [ a, b ] с чебышовской метрикой сходилась к элементу х этого пространства, необходимо и достаточно, чтобы функциональная последовательность (x_n (t))равномерно сходилась к х (t)на [ a, b ].

Докажем достаточность.

3Напомним, что метрика в пространстве С [ a, b ] имеет вид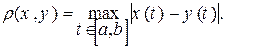

Известно, что функциональная последовательность (x_n) равномерно сходится к предельной функции х тогда и только тогда, когда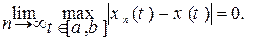

С учетом определения метрики в пространстве С [ a, b ]мы имеем равенство

по метрике r в метрическом пространстве С [ a, b ]. 4

Пример 5.2. x_n (t) = tⁿ " tÎ [0; 1/2] Ù " nÎ N. Известно, что на отрезке [0; 1/2] функциональная последовательность x_n (t) = tⁿ равномерно сходится к предельной функции x (t) = 0. Таким образом " tÎ [0; 1/2] последовательность (x_n) сходится к х = 0 в метрическом пространстве С [0; 1/2].

Теорема 5.4. Если а – предельная точка множества Е метрического пространства (X, r), то существует последовательность (x_n), элементы которой принадлежат Е и не равны а, которая сходится к а в этом метрическом пространстве.

Доказательство аналагично доказательству для пространства R.