Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Определение 2.8. Если множество ЕÌХ содержит все свои предельные точки, то оно называется замкнутым.

Пример 2.8. В пространства R¹ : Е ₁ = (a, b), 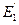= [ a, b ];

E ₂ = [ a, b ], 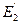= Е₂;

Е ₃ = (2, 4) È {6}; 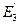= [2, 4].

Пример 2.9. Пустое множество – замкнутое множество.

Определение 2.9. Точка х_о называется изолированной точкой множества Е, если существует e - окрестность этой точки, которая не содержит никаких других точек множества Е, кроме самой точки х _о .

Замечание 2.4. Каждая точка множества Е предельная или изолированная.

Пример 2.10. В метрическом пространстве R каждая точка множества {0, 1, 1/2, …}, кроме точки 0, является изолированной; точка 0 – предельная точка данного множества.

Определение 2.10. Точка х_о называется точкой прикосновения множества Е, если любая его e - окрестность содержит хотя бы одну точку множества Е.

Из определений 2.7, 2.9 и 2.10 следует, что каждая точка прикосновения множества Е может быть

- или предельной точкой множества Е, которая принадлежит множеству Е;

- или предельной точкой множества Е, которая не принадлежит множеству Е;

- или изолированной точкой множества Е.

Определение 2.11. Множество всех точек прикосновения множества Е называется замыканием множества Е и обозначается .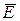

Замечание 2.5. 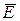= Е È Е¢.

Замечание 2.6. Множество замкнутое, если оно совпадает со своим замыканием.

Определение 2.12. Дополнением множества ЕÌ Х до множества Х называется множество всех точек множества Х, которые не принадлежат множеству Е. Это множества обозначается С_хЕ или СЕ.