Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Определение и примеры метрических пространств

Предисловие

Данное учебно-методическое пособие предназначено студентам-заочникам математического факультета для организации самостоятельной работы и подготовки к зачету и экзамену. В нем содержится теоретический материал раздзела математического анализа “Метрические пространства” и шесть вариантов контрольных работ по тематике разделов математического анализа “Метрические пространства” и “Дифференциальное и интегральное исчисление функции многих переменных”, образец решения нулевого варианта, вопросы к экзамену, список рекомендуемой литературы.

Содержание пособия соответствует программе курса математического анализа.

В пособии использованы распространенные символы математической логики и логические операторы Þ, Û, Î, Ì, ", $.

Для удобства текст, которым начинается и завершается доказательство теорем, показаны значками 3и4соответственно.

Определение и примеры метрических пространств

Известно, что расстояние между двумя точками М ₁(х ₁, y ₁) и М ₂(х ₂, y ₂)плоскости вычисляется по формуле

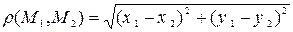
и имеет свойства:

1) r (M ₁, M ₂) ³ 0; r (M ₁, M ₂) = 0 Û M ₁ = M ₂;

2) r (M ₁, M ₂) = r (M ₂, M ₁);

3) r (M ₁, M ₂) £ r (M ₁, M ₃) + r (M ₂, M ₃) (неравенство треугольника).

Напомним, что если имеются два непустых множества X и Y, то их декартовым произведением X´ Y называется множества всех упорядоченных пар . В частности X´ Х обозначается X ².

Обобщим понятие расстояния на любое множества с помощью понятия декартового произведения двух множеств: .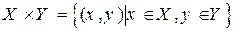

Пусть Х – некоторое непустое множества любой природы. Рассмотрим декартовое произведение .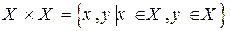

Определение 1.1. Метрикой (расстоянием) на множестве Х называется отображение r декартова произведения Х ´ Х в множества действительных чисел, удовлетворяющее следующим условиям для " x, y, zÎ X:

1) r (x, y) ³ 0; r (x, y) =0 Û x = y;

2) r (x, y) = r (y, x);

3) r (x, y) £ r (x, z) + r (y, z) (неравенство треугольника).

Значение функции r в точке (x, y), т.е. число r (x, y), называется расстоянием между точками x и y. Условия 1-3 называются аксиомами метрики.