Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Классификация точек и множеств в метрических пространствах

Пусть (Х, r) – метрическое пространство.

Определение 2.1. Открытым шаром с центром в точке х _о и радиусом e называется множества всех точек х, которые удовлетворяют условию r (x, х _о) < e. Это множества называется также e -окрестностью точки х_о и обозначается U (x _o, e) или U_e (x_o).

Пример 2.1. Открытый шар в различных пространствах:

- в пространстве R ¹: (x _o- e; x _o + e) – интервал;

- в пространстве R ²: открытый круг;

- в пространстве R ³: открытый шар.

Определение 2.2.Замкнутым шаром с центром в точке х _о и радиусом e называется множества всех точек х, которые удовлетворяют условию r (x, х_о) £ e.

Мы будем говорить шар и будем иметь в виду определение 2.2.

Сфера – множества точек, которые удовлетворяют условию r (x, х _о) = e.

Пример 2.2. Шар в различных пространствах:

- в пространстве R ¹: [ x _o- e; x _o + e ] – отрезок;

- в пространстве R ²: замкнутый круг или просто круг;

- в пространстве R ³: замкнутый шар или шар.

Определение 2.3. Множества ЕÌ Х называется ограниченным в метрическом пространстве(Х, r), если существует шар конечного радиуса, который содержит это множества.

Замечание 2.1. Множества в различных метрических пространствах могут быть ограниченными и неограниченными.

Пример 2.3. Интервал (3; 5) Ì R –ограниченное множество в пространстве R; интервал (3; 5) пространстве Х = ((3; 5), r (x, y) = ½ х-y ½) не является ограниченным в пространстве Х.

Определение 2.4. Пусть ЕÌ Х. Точка х ₀ называется граничной точкой множества Е, если в любой окрестности этой точки содержатся точки, которые принадлежат множеству Е и не принадлежат ему.

Множества граничных точек – граница множества Е и обозначается ¶Е.

Пример 2.4. Множества Е ₁ = (0; 1] Ì R Þ ¶Е = { 0; 1};

множества Е₂ = (0; 1] Ì Х = ((0; 1], r (x, y) = ½ х- в ½) не имеет границы.

Замечание 2.2. Граничные точки множества могут как принадлежать множеству, так и не принадлежать ему.

Определение 2.5. Точка х ₀ называется внутренней точкой множества Е, если существует окрестность точки х ₀, которая целиком содержится в множестве Е. Множество всех внутренних точек называется внутренностью множества Е и обозначается .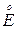

Пример 2.5. Е ₁ = (2; 3), Е ₂ = (2; 3], Е ₃ = [2; 3] Þ 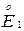= = 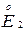= 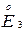(2; 3)

Пример 2.6. в метрическом пространстве R; 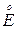= Е в пространстве: Х = ((2, 3]È È {4, 5}, r (x, y) = ½ х-в ½) – подпространство м.пр. R.

Определение 2.6. Если каждая точка множества Е внутренняя, то оно называется открытым, а его внутренность совпадает с самим множеством: 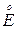= Е.

В примере 2.5 множество Е ₁ является открытым, а множества Е ₂ и Е ₃ не являются открытыми.

В примере 2.6 в первом случае множество Е не является открытым, во втором - является открытым.

Пример 2.7. Интервал (a, b)является открытым множеством в метрическом пространстве R.

Определение 2.7. Точка х _о называется предельной точкой множества Е, если в любой его окрестности содержится бесконечно много точек множества Е.

Другими словами точка х _о называется предельной точкой множества Е, если в любой его окрестности находится хотя бы одна точка множества Е, которая не совпадает с х _о.

Множество всех предельных точек множества Е называется производным множеством множества Е и обозначается Е¢.

Замечание 2.3. Предельные точки могут как принадлежать множеству Е, так и не принадлежать ему.