Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Теоретичний вступ

ЛАБОРАТОРНА РОБОТА №1.

Тема. Дослідження випадкових явищ

Мета: Глибше зрозуміти поняття ентропії, інформації та термодинамічної ймовірності, перевірити закон збереження інформації.

Теоретичний вступ

Оборотні процеси можуть проходити в обох напрямках, тоді як необоротні – тільки в одному. I закон термодинаміки вимагає, щоб загальна енергія не змінилась, тоді як про напрям процесу він нічого не говорить. Напрям процесів встановлює II закон термодинаміки.

Деякі формулювання:

1) Теплота не може самовільно передаватись від менш нагрітого тіла до більш нагрітого, якщо при цьому не відбувається ніяких змін у них або в навколишньому середовищі.

2) Неможливий вічний двигун II роду, який одержував би теплоту від нагрівача і перетворював би її пов­ністю в роботу.

Найбільш загальне формулювання II закону термодинаміки можна зробити на основі по­няття ентропії.

Якщо замкнута система переходить із стану 1 у стан 2, то кількість теплоти Q, яку вона одержує з навколишнього середовища, залежить від шляху. Але, виявляється, що при цьому величина

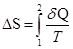(1.1)

не залежить від шляху переходу з одного стану в інший, а тільки від початкового й кінцевого станів, тобто є функцією стану. Тут Т ─ абсолютна температура, 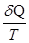─ приведена теплота. Величина S називається ентропією. Одиниця вимірювання ент­ропії [S]=Дж/К. Елементарна кількість теплоти, яку одержує система в оборотному процесі:

δ Q=TdS

В оборотних процесах при передачі теплоти Q системі її ентропія зростає на величину (1.1), а ентропія навко­лишнього середовища – зменшується на таку ж величину, тобто за­гальна ентропія ізольованої системи не міняється.

При необоротних процесах загальна ентропія ізольованої системи завжди зростає, тобто знак зміни ентропії однозначно визначає напрям необоротного процесу. Ентропія системи змі­нюється не тільки за рахунок обміну теплотою з навколишнім середовищем, але й за рахунок незворотних процесів всередині самої системи. Тому елементарна кількість теплоти, яку одер­жує система від навколишнього середовища:

δ Q< TdS (1.2)

Загальна ентропія зростає, поки система не досягне термодинамічної рівноваги. Отже, нерівноважна система завжди прагне до максимуму ентропії.

Формулювання II закону термодинаміки: В ізольованій системі ентропія зберігає по­стійне значення для оборотних процесів, зростає при необоротних процесах і досягає мак­симуму у стані термодинамічної рівнова­ги.

Поняття ентропії насправді значно ширше, ніж показане в (1.1), оскільки ентропія ізо­льованої системи може мінятись і без передачі теплоти. Якщо ізольована система перебуває у нерівноважному стані, то перехід у стан термодинамічної рівноваги – необоротний процес, і супроводжується зростанням ентропії.

Кількість способів, якими можна зреалізувати даний стан, називається термодинамічною ймо­вірністю. Якщо говорити про макромолекули, то вона пропорційна математичній імовірності випадкового розміщення атомів на своїх місцях. Зрозуміло, що найбільшу математичну й термодинамічну ймовірність має стан із хао­тичним, невпорядкованим розміщенням атомів. Стан із найбільшою термодинамічною ймовір­ністю – найбільш імовірний стан. Цей стан і є рівноважним станом. Біомакромолекула чи інша термодинамічна система, залишена сама на себе, необоротно переходить від упорядкованого стану в невпорядкований, при цьому її ентропія зростає. Ентропія є мірою безладдя.

Больцман установив зв'язок між термодинамічною ймовірністю та ентропією:

S=klnW(1.3)

k=1, 36·10^–23 Дж/К – стала Больцмана.

Ізольована система завжди прагне до стану рівноваги, тобто стану з максимальною ент­ропією. Але навіть стану рівноваги притаманні флуктуаці ї – невеликі відхилення параметрів від рівноважних значень.

Система з безладно перемішаних молекул має максимальну ентропію, а організм з упо­рядкованим розміщенням молекул – набагато меншу, причому у процесі росту його ентропія зменшується. Це стає можливим унаслідок того, що організм – не ізольована, а відкрита систе­ма. Ентропія організму зменшується за рахунок зростання ентропії навколишнього середовища, а в кінцевому підсумку – Сонця: його енергія, сконцентрована в межах небесного тіла, безпе­рервно розсіюється в просторі.

Упорядковане розміщення молекул в організмі – це наявність певної інформації I (у ро­зумінні впорядкованості), тоді як безладдя – її повна відсутність. Тому ентропію можна розгля­дати як величину, протилежну до інформації, тобто як міру недостачі інформації про систему. При будь-яких процесах має місце закон збереження:

I+S=const

Одиниця кількості інформації – біт – інформація, яка міститься в достовірному твер­дженні, якщо кількість можливих станів ω =2, тобто математична ймовірність події P=1/2. Вза­галі:

I=–log₂P=log₂(ω /W) (1.4)

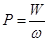
Порівнявши (1.3) і (1.4), маємо: 1 біт=0, 9427·10^–23 Дж/К=0, 22·10^–23 кал/К.

Розглянемо посудину, у лівій половині якої – N₁ молекул, у правій половині – N₂ моле­кул. Якщо всі молекули нерозрізнимі, то загальна кількість способів, якими реалізується стан N₁ – N₂:

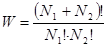
Якщо маємо, наприклад, ситему, яка складається з 6-ти однакових фазових комірок, в яких може бути поміщено деяка кількість частинок, то формула для термодинамічної ймовірності:

де A, B, C, D, E, F ─ кількість частинок в кожній з комірок.

При рівномірному розміщенні частинок по комірках маємо максимальну ентропію і відповідно мінімальну інформацію, чим нерівномірніше (більш впорядковано) розміщені частинки ─ тим менша ентропія, у випадку попадання всіх частинок в одну комірку ентропія системи буде мінімальна, а інформація ─ максимальна.

Прилади і матеріали:

1. Гральні кості.

2. Калькулятор