Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обработка ряда истинных погрешностей измерений
|
|
Истинная погрешность измерений может включать в себя не только случайную погрешность, но и систематическую, либо ряд систематических погрешностей. Если систематическая погрешность постоянно или односторонне действует на результаты многократных измерений, она исключается введением соответствующих поправок. В реальных условиях измерений одновременно могут влиять несколько систематических погрешностей, значение которых определить практически невозможно. В этом случае оценивается их совместное влияние как среднее арифметическое для ряда истинных погрешностей:
θ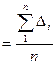 
, где n - число измерений (погрешностей).
При значении θ («тэта»), близком к нулю (сопоставимом с точностью измерений) делается вывод о незначительном влиянии систематической составляющей или ее отсутствии. В противном случае необходимо исключить систематическую погрешность вычитанием величины θ из величин истинных погрешностей Δ i. После исключения систематической части остается случайная составляющая погрешности
η i («эта») = Δ i - θ.
2.1. Вычислить систематическую часть погрешности измерений, исключить ее из приведенных в таблице значений. В заданном ряде из 24 измерений использовать по варианту значения истинных погрешностей для измерений №№ 7, 8, 15, 16, 23, 24.
2.2. Определить среднюю квадратическую погрешность измерений m после исключения систематической составляющей.
2.3. Оценить точность определения средней квадратической погрешности вычислением mm = m /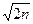 
Значения средних квадратических погрешностей округлить до двух десятичных знаков.
Результаты вычислений оформить в табличной форме:
| № | Δ, см | η | η * η | № | Δ, см | η | η * η |
| изм-я | изм-я | ||||||
| -11 | |||||||
| -3 | |||||||
| -1 | |||||||
| -5 | |||||||
| -3 | -6 | ||||||
| -4 | |||||||
| -3 | -5 | ||||||
| -1 | |||||||
| [Δ ]= | [η ] = | [η *η ] = | |||||
| θ = | m = | mm = |
4. Обработка ряда равноточных измерений одной и той же величины
В соответствии с вариантом обработать результаты равноточных измерений угла наклона (число измерений n = 5):
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
3.1. Вычислить вероятнейшее значение измеренной величины (среднее арифметическое) - хo. Для упрощения вычислений использовать способ «ложного нуля». Для этого наименьшее значение принимают за начало отсчета и вычисляют отклонения от наименьшего значения ε = хi - хmin, а вероятнейшее значение находят по формуле:
хo = хmin + [ε ] / n, где [ε ] - сумма отклонений от наименьшего
3.2. Вычислить среднюю квадратическую погрешность измерения - m;
В таблице буквой δ обозначена вероятнейшая погрешность хi - хo.
3.3. Оценить точность определения среднего арифметического значения вычислением его средней квадратической погрешности М.
| Номер изм-я | Угол хi | ε мин. | δ мин | δ *δ | среднеквадратические погрешности, мин. | ||||
| m = | |||||||||
| M = | |||||||||
| хmin = | [ε ] = | ||||||||
| [δ *δ ] = | |||||||||
| [ε ] / n = | [δ ] = | ||||||||
| хo= |
|
|