Синтез регулятора первого контура и его свойства

Основой синтеза регулятора является расчетная схема САР величины X], изображенная на рис. 28.

Регулятор Фильтр Звено объекта 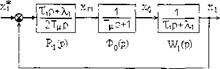Рис. 28 Расчетная схема системы регулирования величины X1

Здесь показана замкнутая система с регулированием по отклонению, элементами которой являются регулятор, фильтр и звено объекта. Передаточные функции этих элементов обозначаются соответственно как R₁(p), Ф₀(р) и W₁(p). Датчик регулируемой величины X₁ обеспечивает единичную обратную связь замкнутой САР.

В задаче синтеза регулятора заданной частью системы являются фильтр и звено объекта с передаточными функциями вида:

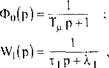
где Тμ - нскомпенсируемая постоянная времени, выбираемая

исходя из требуемого быстродействия и помехоустойчивости системы регулирования;

Т_1p - параметры звена объекта, попадающего в первый контур регулирования.

Последняя формула описывает при основных типа звеньев объекта регулирования.

Если τ ₁> 0 и λ ₁=0 то звено является апериодическим. В этом случае параметры звена объекта определяются как

λ ₁^-1 – коэффициент усиления

τ ₁ λ ₁^-1 - постоянная времени .

Если τ ₁> 0, λ ₁=0, то 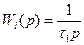т.е звено является интегрирующим

Если τ ₁₌0, λ ₁> 0, то т.е звено является усилительным

К числу элементов САР с известными параметрами отнесем также датчик регулируемой величины. Напомним, что нами принято D_i(p) = 1, т.е. рассматривается система с безынерционной единичной

обратной связью по величине X_1.

Структура и параметры регулятора величины X₁ выбираются исходя из решения трех перечисленных выше основных задач.

Для решения первой задачи (компенсации действия звена объекта методом последовательной коррекции) в структуру регулятора вводится звено, передаточная функция которого обратна по отношению к передаточной функции компенсируемого звена:

R_K1(p) = [W₁(p)]^-1

Для решения второй задачи (обеспечения аетатизма) в структуру регулятора последовательно вводится интегрирующее звено:

R_u1(p) =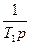

В соответствии с изложенными принципами общий вид передаточной функции регулятора определяется формулой:

R₁(p) = [W₁(p)]^-1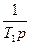

Итак, в структурном отношении регулятор состоит из двух частей: компенсирующей и интегрирующей.

Следующий этап синтеза регулятора заключается в определении его параметров, оптимизирующих процессы регулирования по некоторому критерию. Параметры компенсирующей части регулятора полностью определяются параметрами объекта. Поэтому единственным варьируемым параметром регулятора, который может быть использован для оптимизации процесса, является постоянная времени его интегрирующего звена Т₁. Эту

величину удобно выражать в долях от некомпенсируемой постоянной времени T_μ , используя коэффициент α ₁

Т₁ = α ₁ T_μ

На рис. 29. показаны реакции САР на ступенчатое задающее воздействие при различных соотношениях постоянной времени интегрирующего звена регулятора и некомпенсируемой постоянной времени. При выборе коэффициента α ₁ < < l т.е. при Т₁ < < T_μ реакция системы на типовое задающее воздействие протекает относительно быстро, но имеет сильно колебательный характер (кривая 1). При выборе α ₁> > 1, т.е. Т₁ > > T_μ переходный процесс протекает гораздо медленнее и носит апериодический характер (кривая 3). Оптимальным вариантом настройки регулятора считается такой, при котором α ₁ =2, то есть 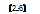Т₁= T_μ ,

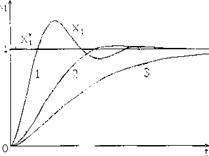
Этот вариант настройки регулятора по существу является компромиссным, удачно сочетающим достаточно высокую скорость протекания процесса с одной стороны и небольшое перерегулирование с другой (кривая 2 рис. 2..4). Такой вариант настройки системы носит специальное название; настройка на технический или модульный оптимум. Рассмотрим подробнее основные свойства системы, настроенной на модульный оптимум. С этой целью проведем эксперимент, схема которого и зображена на рис. 2.4.

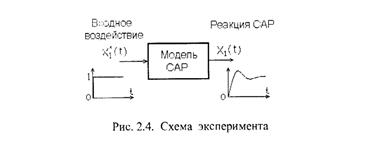
Математически эксперимент описывается следующим образом. Пусть входной сигнал представляет собой единичную ступенчатую функцию времени:

X₁^*(t)=1(t)

Тогда при нулевых начальных условиях реакция САР описывается следующим выражением:

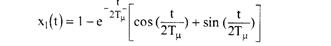
График переходного процесса, характеризующего реакцию САР на скачок управляющего воздействия, изображен на рис. 2.5.

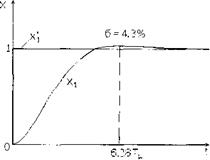Рис. 2.5. График переходного процесса при настройке первой САР на модульный оптимум

Основные показатели переходного процесса при настройке системы на модульный оптимум следующие:

· время первого согласования 4.7T μ

· время достижения максимума 6.28 T μ

· время достижения зоны 5% 4.1 T μ

· отклонения время достижения зоны 1% 8 T μ

· отклонения перерегулирование 4.3 T μ

На практике эти показатели служат определенным стандартом, которому должна удовлетворять оптимально настроенная система.

Таким образом, оптимальная настройка регулятора обеспечивает переходный процесс с незначительным перерегулированием σ = 4.3% и реальной длительностью отработки задания (оцениваемой по времени достижения максимума) порядка 6.28 T μ.

Отсюда следует важный вывод о том, что благодаря компенсирующему действию регулятора быстродействие системы не зависит от параметров объекта регулирования и полностью определяется выбранной величиной базовой (некомпенсируемой) постоянной времени T μ. Поэтому величина T μ

может быть использована в качестве инструмента для достижения необходимого быстродействия САР при сохранении стандартного перерегулирования.

Для синтеза последующих регуляторов необходимо определение передаточной функции замкнутой системы регулирования величины как элемента, подчиненного следующему регулятору. Сначала найдем передаточную функцию разомкнутой системы:

В итоге получаем ныражение, характеризующее стандартную передаточную функцию разомкнутой системы, настроенной на модульный оптимум:

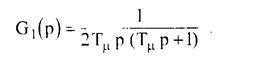
Пользуясь известной из теории автоматического регулирования [5] формулой замыкания системы единичной отрицательной обратной связью

найдем передаточную функцию замкнутой системы, настроенной на модульный оптимум:

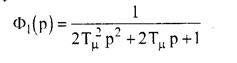
Это выражение можно представить в так называемой канонической форме

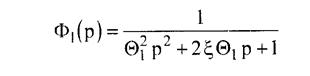
Она характеризует рассмотренную САР, как оптимально демпфированную систему второго порядка с постоянной времени Θ ₁ = 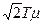и коэффициентом демпфирования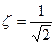