Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Якщоnнепарне, то функція f(x)в точці x0 екстремуму не має.

Дослідити на екстремум функцію

f (x) = х ³ – 3 х ² + 3 х +5. ·

· Знаходимо похідну f¢ (x) = 3 х ² – 6 х + 3. Рівняння f¢ (x) = 0 має одну стаціонарну точку х = 1, тому f¢ (1) = 0. Далі,

.

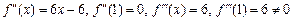Отже, f ¢ (1) = f ² (1) = 0, але f ² ¢ (1) ¹ 0. За теоремою в стаціонарній точці х = 1 функція f (x) екстремуму не має.

.

45. Асимптоти кривої

Означення. Асимптотою кривої називають пряму (або криву) лінію, до якої необмежено наближається точка, рухаючись по кривій у нескінченність.

Рис. 5.45

1. Вертикальні асимптоти. Нехай функція 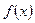визначена в одному з інтервалів (а; с) та (с; b), або на обох із них, причому
с — скінченне число.

Означення. Якщо функція 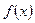має в точці с розрив другого роду і існує хоча б одна із нескінченних односторонніх границь функції 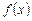в точці с (наприклад, 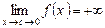або 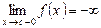, рис. 5.45), то пряму х = с називають вертикальною асимптотою кривої .

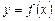Отже, усі вертикальні асимптоти виду х = с кривої 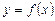можна знайти, знайшовши скінченне число точок с, в яких функція 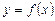має розриви другого роду й існує хоча б одна із нескінченних односторонніх границь функції f (x) у точці с.

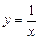Функція має вертикальну асимптоту 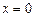(рис. 5.46), оскільки точка 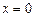— точка розриву другого роду:

; .

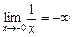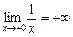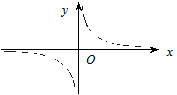
Рис. 5.46

Графік функції має вертикальні асимптоти 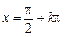(рис. 5.47).

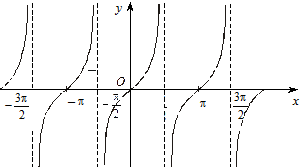
Рис. 5.47