Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Теорема 3 (друга ознака опуклості функції). Якщо f(x) опукла в інтервалі (a; b), то для будь-якої точки х0 Î (a; b) функція

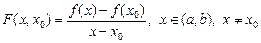, (4)

Монотонно зростаюча по х (неспадна). Якщо функція f(x) строго опукла, то F(x, x0) — строго зростаюча.

Справджується й обернена теорема.

Теорема 4. Якщо функціяf(x)задана в інтервалі(а; b)і для будь-якої точки функція

,

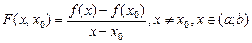неспадна, то f (x) опукла (а; b), якщо 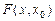строго зростаюча, то f (x) строго опукла на (а; b).

Теорема 5 (третя ознака опуклості функції). Функція f (x) строго опукла в інтервалі (а; b) тоді і тільки тоді, коли для будь-яких х ₁ < x ₂ < x ₃ із (а; b).

.

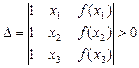Очевидно, що 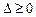є критерієм для опуклої функції.

37. Критерії опуклості та вгнутості
диференційовних функцій

Теорема 1. Для того щоб диференційовна в інтервалі(a; b)функціяf(x)була опуклою (вгнутою), необхідно і достатньо, щоб її похіднаf¢ (x)у цьому інтервалі була монотонно зростаючою (монотонно спадною).

Дослідити функцію 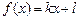на опуклість.

● Маємо 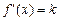і похідну f¢ (x) можна вважати і неспадною, і незростаючою. Тому функція f (x) опукла і вгнута не в строгому розумінні. ●

Знайти проміжки опуклості і вгнутості функції

.

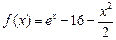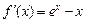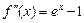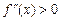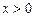● Оскільки , то задача зводиться до знаходження проміжків монотонності похідної f¢ (x). Скориставшись умовами монотонності, знайдемо, що , звідки робимо висновки, що для і 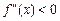для х < 0.

Отже, f¢ (x) зростає на проміжку (0; + ¥) і спадає на проміжку (–¥; 0). Звідси функція f (x) строго опукла на проміжну (0; + ¥) і спадає на проміжку (–¥; 0).

Теорема 2. Нехай функція f (x) двічі диференційовна на проміжку [ a; b ].

1) Для того щоб функція f (x) була опуклою (вгнутою) на проміжку [ a; b ], необхідно і достатньо, щоб 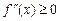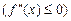для будь-якого х Î [ a; b ].

Для того щобf(x)була строго опуклою (строго вгнутою) на проміжку[a; b], необхідно і достатньо, щоб виконувалась попередня умова і щоб, крім того, не існувало інтервалу (с; d)Ì [a; b], в якому.

Означення. Диференційовна функція f (x) називається опуклою (вгнутою) в інтервалі (a; b), якщо в будь-якій точці графіка функції f (x) із інтервалу (a; b) дотична до графіка лежить не вище (не нижче) від графіка функції (рис. 5.27).

Означення. Диференційовна функція f (x) називається строго опуклою (строго вгнутою) в інтервалі (a; b), якщо в будь-якій точці графіка функції f (x) із інтервалу (a; b) дотична до графіка лежить нижче (вище) графіка функції f (x).