Принцип функционирования и математическая модель сигнала бортового радиовысотомера.

Принцип функционирования радиовысотомеров. Радиовысотомеры предназначены для измерения высоты полета ЛА относительно рельефа местности. Их работа основана на использовании сигналов, отраженных от земной поверхности. Потенциальные возможности радиовысотомеров во многом определяются статистическими характеристиками отраженных сигналов.

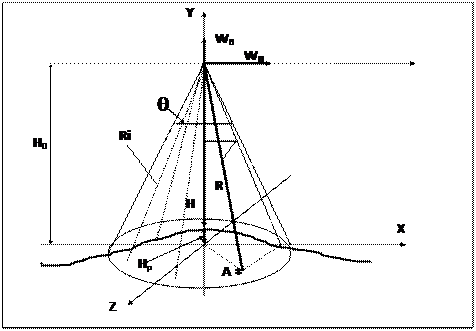
Поясним принцип функционирования РВ и источники погрешностей измерения с помощью приведенного выше рисунка.

Для обеспечения работоспособности РВ при наличии углов крена и тангажа ЛА, с целью исключения потерь сигнала в процессе пространственного маневрирования, у них используются антенны с широкими диаграммами направленности. Специфика отражения радиосигнала в диапазоне частот, в котором работают РВ заключается в том, что в результате отражения зондирующего сигнала от протяженной поверхности случайного поля рельефа полезный сигнал на входе бортового приемника представляет собой результат наложения большого количества элементарных сигналов, отраженных от точек, расположенных в пределах облучаемой площади.

То есть в отраженном сигнале заложена информация не только о высоте полета H, но и о различных наклонных дальностях Ri. в пределах зоны, ограниченной диаграммой направленности антенны РВ. Основой для измерения высоты с помощью радиовысотомеров служат временные задержки отраженного сигнала, величина которых зависит от значения наклонной дальности. Вопрос заключается в том, какое именно значение наклонной дальности (при том что в структуре отраженного сигнала содержится информация соответствующая наклонным дальностям до различных точек поверхности в пределах диаграммы направленности) использовать для последующих оценок временных задержек, а на их основе оценок высоты полета ЛА.

В РВ для измерения высоты по временной задержке отраженного сигнала полагается, что её значение соответствует не истинной высоте H, а некоторой наклонной дальности R до кажущегося точечного источника отраженного сигнала (так называемого эффективного центра отражения). Эффективный центр отражения обозначен точкой А.

При этом полагается, что положение эффективного центра отражения случайно и характеризуется наклонной дальностью R_a(t) и двумя углами u_a(t), g_a(t). Угол u_a(t) отсчитывается в вертикальной плоскости, проходящей через вектор W_П путевой скорости ЛА. Угол g_a(t) отсчитывается в плоскости проходящей через R_a(t) и перпендикулярной плоскости отсчета угла u_a(t). Угол qa характеризует ширину диаграммы направленности излучающей антенны.

Координаты точки, рассматриваемой в качестве эффективного центра отражения, а следовательно значение соответствующей ей наклонной дальности зависит от статистических свойств отражающей поверхности, характеристики диаграммы направленности антенны, параметров зондирующего сигнала и способа обработки принятого сигнала.

Известны два способа обработки отраженного сигнала, используемые для выделения высоты- локальный и интегральный.

При локальных способах обрабатывается часть отраженного сигнала, соответствующая участкам поверхности, лежащим в окрестности нормали Н. При этом положение эффективного центра отражения соответствует максимуму огибающей частотного спектра отраженного сигнала

При таком способе обработке наклонная дальность до эффективного центра отражения рассчитывается по частоте, соответствующей максимуму огибающей отраженного сигнала.

При интегральных способах для получения информации о высоте используется весь отраженный сигнал. При этом временная задержка соответствует задержке центра тяжести огибающей спектра отраженного сигнала.

Математические модели параметров сигнала радиовысотомера. Предполагается, что отраженный сигнал поступающий на вход радиовысотомера может быть представлен в следующем виде:

S(t)= Acos[w₀t + Dw/Wcos(Wt - 2/cR(t))+j(t)],

где - R(t) наклонная дальность до эффективного центра отражения; Наклонная дальность R(t) связана с высотой полета Н(t) относиельно рельефа и углами u_a(t), g_a(t) определяющими положение эффективного центра отражения соотношением:

R(t)= H(t)/[cosu_a(t)cosg_a(t)]

A, w₀, Dw, W- параметры отраженного сигнала, предполагаемые известными; j(t)- случайная фаза отраженного сигнала.

С учетом приведенного соотношения отраженный сигнал, поступающий на вход приемника радиовысотомера можно представить в виде:

S(t)= Acos[w₀t + Dw/W cos(Wt - (2/c)H(t)/cosu_a(t)cosg_a(t))+j(t)],

Рассмотрим соотношения, используемые для описания параметров отраженного сигнала.

Изменение во времени высоты полета ЛА относительно рельефа определяется как характером движения ЛА, так и изменением крупномасштабного профиля поверхности:

Н(t)= H₀(t)- H_Р(t),

где H₀(t)- высота полета относительно некоторого среднего уровня рельефа поверхности; H_Р(t) - случайные колебания профиля поверхности относительно среднего уровня. Характеристики случайных колебаний профиля поверхности определяются на основе анализа топографических карт. Строго говоря из-за большого разнообразия реальных профилей случайные колебания H_Р(t) невозможно описать единой моделью. Поэтому используют несколько типовых моделей поверхности суши и моря. К ним относятся:

1) Модель в виде гладкой поверхности. Естественных поверхностей подобного типа в природе крайне мало. Примером такой поверхности могут служить водная поверхность при абсолютном безветрии. Колебания для такой поверхности описываются уравнением H_Р(t)=0

2) Модель в виде среднеплоской поверхность. Подобная модель, известная как мелкомасштабная, используется для описания бетонных, песчаных, гравийных покрытий, высохших соляных озер, участков выхода скальных пород, водные поверхности с небольшой рябью.

3) Крупномасштабная модель. Используется для описания основных рельефов суши: невспаханные поля, холмистая местность, пустыни с барханами, обломки скал, большие волны морской поверхности.

4) Модель поверхности со сложной шероховатостью. Подобные модели могут использоваться для описания вспаханной холмистой местности, участки пустынь с крупными барханами и песчаной рябью, волнения морской поверхности в виде сочетания крупных и мелких волн.

5) Модель для поверхностей с разрывным профилем. Обычно подобная модель используется для описания поверхностей с разнообразным рпастительным покровом: культурные посадки, кустарники, лес и.т.д. В этом случае на характеристики отраженного сигнала существенное влияние оказывают густота растительного покрова, его высота, влагосодержание и.т.д. Подобные модели также используются для описания поверхностей с населенными пунктами, отдельностоящими горами.

Наиболее часто в системах обработки информации радиовысотомеров используют крупномасштабную модель. В рамках такой модели случайные колебания H_Р(t) описываются гауссовским случайным процессом, корреляционная функция которого в направлении полета ЛА описывается соотношением следующего вида:

К_Р(DZ) = s²(1+1/r½ DZ ½)exp{-1/r½ DZ ½ },

где s² - среднеквадратическое отклонение высоты рельефа поверхности относительно среднего уровня; r - радиус пространственной корреляции профиля поверхности. Указанные значения для некоторых типовых профилей поверхности равны:

1) для среднепересеченного рельефа: s² =10-20м; r = 2-3 км

2) для горного плато s² =100-300м; r = 200-800 м

В рамках такого представления случайные колебания высоты рельефа поверхности могут быть описаны системой стохастических дифференциальных уравнений вида:

dH_Р/dt= H’_Р(t)

dH’_Р/dt= -2mH’_Р(t) -m²H_Р(t)+(4m³s²_Р)^1/2 n_p(t),

где m=W_П/r; n_p(t) - формирующий гауссовский белый шум с нулевым математическим ожиданием и единичной интенсивностью

Изменение во времени случайных углов u_a(t), g_a(t) определяющих положение эффективного центра отражения описывается системой дифференциальных стохастических уравнений вида:

du_a(t)/dt = -hu_a(t)+ (2hs²_u)^1/2n_u(t)

dg_a(t)/dt = -hg_a(t) +(2hs²_g)^1/2n_g(t)

где - n_u(t), n_g(t) взаимонезависимые формирующие белые гауссовские шумы с нулевыми математическими ожиданиями и единичными интенсивностями; s²_u, s²_g) -дисперсии отклонений углов u_a(t), g_a(t). Считается, что с достаточной степенью точности можно положить равными s²_u=s²_g =q/2

Изменение случайной фазы отраженного сигнала описывается стохастическим дифференциальным уравнением:

dj(t)/dt =2w₀/с[W_Пsinu_a(t) - W_Вcosu_a(t)] + (N_u)^1/2n_j(t)

Модель измерений высоты. Реализация алгоритмов оптимальной обработки сигналов навигационных устройств опирается на определенную модель измерений, которая связывает параметры сигнала и параметры состояния ЛА. При обработке сигналов высотомеров предполагается что состояние центра масс маневрирующего ЛА может быть описано системой дифф. уравнений:

dH₀/dt=W_В(t)

dW_В/dt=a(t)

da(t)/dt=-(a+b)a(t)- abW_В(t)+(2a²bs²_a)^1/2 n_a(t),

a, b- известные коэфициенты

- s²_a среднеквадратическое отклонение случайной составляющей скорости ветра

Используя связь

Н(t)= H₀(t)- H_Р(t),

изменение высоты можно описать с помошью системы дифференциальных уравнений:

dH/dt=W_В(t) - H’_Р(t)=V(t);

dV(t)/dt=a(t)+2mH’_Р(t)+m²H_Р(t)-(4m³s²_Р)^1/2 n_p(t),

dH_Р/dt= H’_Р(t)

dH’_Р/dt= -2mH’_Р(t) -m²H_Р(t)+(4m³s²_Р)^1/2 n_p(t),

da(t)/dt=-(a+b)a(t)- ab(H’_Р(t)+V(t))+(2a²bs²_a)^1/2 n_a(t),