Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Способ компенсации.

Проиллюстрируем способ компенсации на примере объединения двух НИ, каждый из которых измеряет один и тот же навигационный параметр X(t). На выходе первого измерителя имеется сигнал: Х1(t) = X(t) + N1(t), на выходе второго- сигнал Х2(t) = X(t) + N2(t), X(t) - истинное значение навигационного параметра (полезный сигнал) N1(t), N2(t), -ошибки полагаемые стационарными гауссовскими процессами. (Стационарным называется случайный процесс математическое ожидание и дисперсия которого являются постоянными величинами, не зависящими от времени). Спектральные плотности S1(w), S2(w) ошибок предполагаются известными.

При комплексной обработке навигационной информации по способу компенсации сигналы Х1(t), Х2(t) подаются на вычитающее устройство, с выхода которого сигнал ХА(t)= N1(t) - N2(t) поступает на оптимальный линейный фильтр (ОФ) передаточная функция которого F(p). Тогда сигнал ХВ(p) на выходе фильтра с передаточной функцией F(p) имеет вид:

ХВ(р)= ХА(р) F(p) = (N1(р) - N2(р)) F(p)

Сигнал ХВ(p) сформированный на выходе фильтра в свою очередь подается на другое вычитающее устройство, где формируется разность:

Y(р)= Х1(р)- ХА(р) = Х(р)+ N1(р) -(N1(р) - N2(р)) F(p)=

Х(р)+ (1- F(p))N1(р)+ F(p) N2(р)

Обозначим Ф(р)=1-F(p). Тогда выходной сигнал Y(р) можно представить в виде:

Y(р)= Х(р)+ e(р),

где e(р)-результирующая ошибка

e(р)= e1(р)+ e2(р).

e1(р) = (1- F(p))N1(р)= Ф(р) N1(р)

e2(р) = F(p))N2(р)

В идеальном случае передаточная функция F(p) оптимального фильтра должна выбираться таким образом, чтобы обеспечить минимум дисперсии результирующей ошибки e(t). Однако, на практике исходя из требований практической реализуемости систем комплексной обработки информации, обычно не используют оптимальный фильтр, а выбирают его передаточную функцию так, чтобы результирующая ошибка e(t) была существенно меньше, чем ошибки отдельных измерителей N1(t), N2(t).

Покажем, как за счет выбора передаточной функции F(p) в рамках рассматриваемой схемы объединения НИ можно добиться уменьшения дисперсии результирующей ошибки e(t) по сравнению с дисперсиями отдельных измерителей N1(t), N2(t)., то есть добиться повышения точности определения навигационного пааметра.

Предположим, что спектральные плотности S1(w), S2(w) ошибок N1(t), N2(t) имеют вид, изображенный на рисунке.

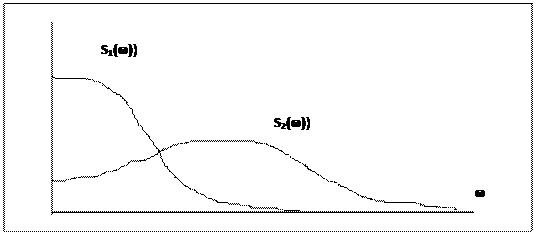
(Cпектральная плотность характеризует изменение дисперсии стационарного случайного процесса по частоте). Следовательно, дисперсии ошибок N1(t), N2(t) рассчитываются через спектральные плотности S1(w), S2(w) следующим образом:

¥

s21 =1/2p ò S1(w)dw

¥

s22 =1/2p ò S2(w)dw

Иначе говоря дисперсии s21 s22 есть ни что иное как площади под кривыми соответствующих спектральных плотностей.

Оценим дисперсию результирующей ошибки. Напомню, что в соответствии с рассматриваемой схемой комплексирования результирующая ошибка e= e1+ e2, где компонента e1 характеризует ошибку, полученную в результате прохождения стационарного случайного процесса N1(t) через линейный фильтр, описываемый амплитудно-частотной характеристикой Ф(jw)=1-F(jw). а компонента e2 характеризует ошибку, полученную в результате прохождения стационарного случайного процесса N2(t), через линейный фильтр, описываемый амплитудно-частотной характеристикой F(jw).

Тогда дисперсия результирующей ошибки может быть рассчитана следующим образом:

¥

s2e =1/2p ò [S1(w)½ Ф(jw)½ 2 + S2(w)½ F(jw)½ 2 ] dw

Какой же должна быть амплитудно-частотная характеристика оптимального линейного фильтра, чтобы дисперсия суммарной ошибки в результате комплексной обработки информации была существенно меньше, чем ошибки отдельных измерителей. Чтобы ответить на этот вопрос рассмотрим идеальный случай, когда спектральные плотности не пересекаются S1(w), S2(w). Тогда, поскольку дисперсия ошибки N1(t) сосредоточена в области нижних частот, а дисперсия ошибки N2(t) сосредоточена в области высоких частот, следовательно, логично в качестве оптимального фильтра F рассматривать - некоторый фильтр нижних частот, амплитудно-частотная характеристика F(jw) которого имеет вид, изображенный на рисунке. Тогда фильтр Ф, амплитудно частотная характеристика которого Ф(jw)= 1-F(jw) будет фильтром верхних частот.

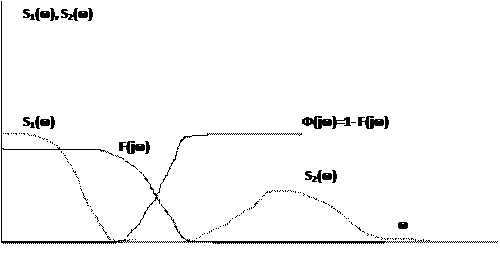
Нетрудно убедиться, что при таком выборе характеристик оптимального фильтра на выходе комплексной системы формируется сигнал Y(t) который без ошибки воспроизводит навигационный параметр X(t). Действительно в этом случае слагаемые подинтегрального выражения для определения дисперсии суммарной ошибки равны 0:

S1(w)½ Ф(jw)½ 2 =0 при любом w

S2(w)½ F(jw)½ 2 =0 при любом w

а значит дисперсия суммарной ошибки

s2e =0

Однако на практике рассмотренная нами идеальная ситуация является достаточно редкой, обычно спектральные плотности S1(w), S2(w) перекрываются, поэтому в выходном сигнале Y(t) присутствует ошибка e= e1+ e2, дисперсия которой определяется в соответствии с приведенным ранее выражением. Оказывается, что использование в подобной ситуации в качестве линейного фильтра F фильтра нижних частот, а в качестве фильтра Ф фильтра верхних частот хотя и не позволяет полностью компенсировать суммарную ошибку измерения, тем не менее позволяет добиться существенного уменьшения дисперсии результирующей ошибки e(t) по сравнению с дисперсиями отдельных измерителей N1(t), N2(t). Проиллюстрируем эту ситуацию: