
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Цилиндрических заготовок. При радиальном СВС-прессовании дно матрицы имеет сложный контур и состоит из двух участков: цилиндрического канала и расположенного по обе стороны от него
|
|
При радиальном СВС-прессовании дно матрицы имеет сложный контур и состоит из двух участков: цилиндрического канала и расположенного по обе стороны от него плоского дна, являющегося основанием песчаной оболочки (см. рис. 7.1, а). При неплоском верхнем или нижнем контуре закрытой матрицы уплотнение порошкового материала происходит неравномерно, что обусловлено различной высотой отдельных участков изделия [160, 161, 238]. В этих работах изучалось течение и распределение плотности в направлении, перпендикулярном оси прессования, которой является ось у. В работе [79] и настоящем разделе впервые выполнено исследование закономерностей уплотнения вдоль оси прессования.
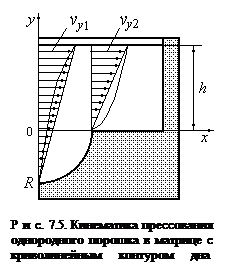
Сначала рассмотрим прессование однородного порошкового материала в матрице с криволинейным профилем дна (рис. 7.5). Процесс деформирования будем описывать по теории пластического течения сжимаемых тел. Тензор скоростей деформации eij связан со скоростью vi соотношениями Коши:
 . (7.5)
. (7.5)
Скорость деформации вдоль оси прессования у будет равна
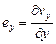 . (7.6)
. (7.6)
Выполним качественный анализ поля скоростей. Для этого используем метод плоских сечений, согласно которому скорость течения порошка в направлении прессования vy линейна по у, а в перпендикулярном ему направлении скорость vх от координаты у не зависит [161]. Это означает, что в вертикальном слое бесконечно малой ширины скорость уплотнения по оси у является постоянной величиной: еу = const. Тогда из выражения (7.6) следует
 , (7.7)
, (7.7)
где С 1, С 2 – постоянные интегрирования. Функция vу (у) должна удовлетворять кинематическим граничным условиям: на пуансоне
vу = - v 0, где v 0 – скорость движения пуансона; на неподвижном дне матрицы vу = 0.
Рассмотрим два сечения: сечение 1 – на оси прессования (х = 0) и сечение 2 – на границе цилиндрического и плоского дна (х = R).
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 Из уравнения (7.7) с учетом граничных условий для сечений 1 и 2 получим
Из уравнения (7.7) с учетом граничных условий для сечений 1 и 2 получим
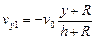 ;
; 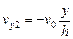 .(7.8)
.(7.8)
Распределение скорости vу (у) при однородном деформировании в характерных сечениях показано на рис. 7.5. При сопоставлении зависимостей vу 1(у) и vу 2(у) несложно заметить, что при одном и том же значении координаты у быстрее движутся частицы в сечении с большей высотой деформируемого объема:
vу 1(у) > vу 2(у). Поскольку порошок рассматривается как сплошная среда, то при неразрывном поле скоростей будет происходить торможение в зонах с большой высотой и ускорение в зонах с малой высотой деформируемого объема, причем кинематические граничные условия для функций vу (у) остаются прежними. В результате зависимость vу (у) будет криволинейной, а деформирование и уплотнение в матрице с неплоским основанием – неоднородным. Примерный схематический вид нелинейных зависимостей vу 1(у) и vу 2(у) показан на рис. 7.5.
О качественном характере уплотнения можно судить по виду зависимости vу (у). Если кривая vу (у) обращена к оси у выпуклостью, то при удалении от пуансона скорость деформации еу уменьшается. Соответственно плотность верхних объемов прессовки будет больше плотности нижних объемов прессовки. Напротив, если кривая vу (у) обращена к оси у вогнутостью, то при удалении от пуансона скорость деформации еу будет увеличиваться. В этом случае более плотными будут объемы, находящиеся в нижней части прессовки.
Гипотеза плоских сечений позволила выполнить только качественный анализ характера деформирования и уплотнения однородного порошкового материала в закрытой матрице с криволинейным контуром дна. При СВС-прессовании совместно деформируются два порошковых тела, имеющие различные реологические свойства. Для этого случая анализ закономерностей уплотнения был выполнен в ходе решения краевой задачи плоского пластического деформирования пористого цилиндра и песчаной оболочки.
Рассматривался процесс радиального прессования цилиндра из твердого сплава TiВ-40% Ti радиусом R 1 = 18, 5 мм. Толщина слоя оболочки над заготовкой составляла 15 мм, ширина оболочки – а об=15 мм. Начальная относительная плотность заготовки принималась равной r 10 = 0, 5 (здесь и далее параметры, относящиеся к заготовке, имеют индекс 1, к оболочке – индекс 2). В качестве характеристики скорости уплотнения рассматривалась скорость изменения объема е, которая при плоской деформации равна сумме скоростей деформации по координатам х и у: е = ех + еу.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
На рис. 7.6 приведены расчетные данные о распределении скорости  , скорости объемной деформации
, скорости объемной деформации 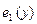 и относительной плотности r1 вдоль вертикальной оси заготовки (х = 0) на разных стадиях прессования. Аналогичные зависимости для оболочки в сечении х = R 1 представлены на рис. 7.7.
и относительной плотности r1 вдоль вертикальной оси заготовки (х = 0) на разных стадиях прессования. Аналогичные зависимости для оболочки в сечении х = R 1 представлены на рис. 7.7.
На начальной стадии прессования (давление прессования q £ 100 МПа) характер зависимостей  и
и  , полученных из решения краевой задачи, соответствует зависимостям
, полученных из решения краевой задачи, соответствует зависимостям  и
и  , вытекающим из качественного кинематического анализа по модели плоских сечений.
, вытекающим из качественного кинематического анализа по модели плоских сечений.
 Высота уплотняемого объема на оси заготовки больше, чем высота оболочки над плоским дном. Соответственно заготовка является «быстроходным» элементом, а боковая зона оболочки – «тихоходным» элементом. В результате взаимодействия квази-
Высота уплотняемого объема на оси заготовки больше, чем высота оболочки над плоским дном. Соответственно заготовка является «быстроходным» элементом, а боковая зона оболочки – «тихоходным» элементом. В результате взаимодействия квази-
сплошных сред с различными кинематическими характеристиками в заготовке и оболочке формируется нелинейное поле скоростей. В заготовке происходит торможение, и кривая  к оси у обращена выпуклостью (см. рис. 7.6, а). Скорость объемной деформации е 1 верхних зон заготовки выше, чем нижних зон (см. рис. 7.6, б), и верхняя часть заготовки имеет более высокую плотность, чем нижняя (см. рис. 7.6, в).
к оси у обращена выпуклостью (см. рис. 7.6, а). Скорость объемной деформации е 1 верхних зон заготовки выше, чем нижних зон (см. рис. 7.6, б), и верхняя часть заготовки имеет более высокую плотность, чем нижняя (см. рис. 7.6, в).
В оболочке кривая  к оси у обращена вогнутостью
к оси у обращена вогнутостью
(см. рис 7.7, а). Поэтому нижняя часть оболочки деформируется и уплотняется более интенсивно, чем верхняя часть
(см. рис. 7.7 б, в). По мере уплотнения верхней части заготовки и нижней части оболочки изменяется характер зависимостей vу (у): кривая  к оси у обращается вогнутостью, а кривая
к оси у обращается вогнутостью, а кривая 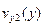 – выпуклостью. Соответственно трансформируются кривые скорости объемной деформации е 1(у) и е 2(у).
– выпуклостью. Соответственно трансформируются кривые скорости объемной деформации е 1(у) и е 2(у).

 В заготовке начинает увеличиваться скорость уплотнения нижней части, а в оболочке – верхней части. После достижения беспористого состояния характерные зоны заготовки и оболочки становятся несжимаемыми, и скорость деформации в них уменьшается до нуля (кривые 3 на рис. 7.6, б и рис. 7.7, б). Расчеты выполнены для давления прессования q = 200 МПа, которое является предельным для штатной инструментальной оснастки радиального СВС-прессования. При дальнейшем росте давления прессования q следует ожидать расширения беспористых несжимаемых объемов сверху вниз в заготовке и снизу вверх в оболочке.
В заготовке начинает увеличиваться скорость уплотнения нижней части, а в оболочке – верхней части. После достижения беспористого состояния характерные зоны заготовки и оболочки становятся несжимаемыми, и скорость деформации в них уменьшается до нуля (кривые 3 на рис. 7.6, б и рис. 7.7, б). Расчеты выполнены для давления прессования q = 200 МПа, которое является предельным для штатной инструментальной оснастки радиального СВС-прессования. При дальнейшем росте давления прессования q следует ожидать расширения беспористых несжимаемых объемов сверху вниз в заготовке и снизу вверх в оболочке.
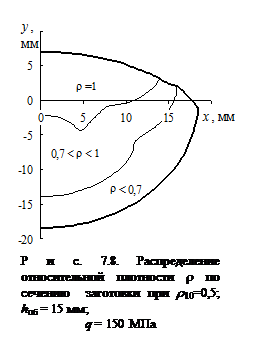 На рис. 7.8 показано расчетное распределение относительной плотности r 1 по сечению заготовки. Согласно результатам расчета в верхней части заготовки образуется беспористая зона с r 1 = 1, которая заканчивается на глубине ~ 2, 5 мм от диаметрального сечения с у =0. Далее плотность уменьшается, и наименьший уровень плотности соответствует донной части заготовки.
На рис. 7.8 показано расчетное распределение относительной плотности r 1 по сечению заготовки. Согласно результатам расчета в верхней части заготовки образуется беспористая зона с r 1 = 1, которая заканчивается на глубине ~ 2, 5 мм от диаметрального сечения с у =0. Далее плотность уменьшается, и наименьший уровень плотности соответствует донной части заготовки.
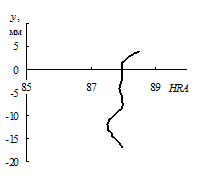
Представляет интерес исследование влияния начальной относительной плотности r 10 на характер уплотнения заготовки. С увеличением r10 увеличиваются размеры беспористой зоны и плотность заготовки в целом (рис. 7.9, а). При начальной относительной плотности r 10 = 0, 6 практически по всей высоте заготовка уплотняется до беспористого состояния. Экспериментальные данные по распределению твердости HRA вдоль оси спрессованной заготовки (рис. 7.9, б) показывают хорошую корреляцию с результатами расчета плотности: по всей высоте заготовки наблюдается почти равномерное распределение твердости. Максимальная величина твердости составляет HRA 88, 5; минимальная – HRA 87, 5.
Неоднородное поле скоростей и скоростей деформаций приводит к формированию неоднородного поля плотности и свойств по сечению спрессованной заготовки. С точки зрения получения конструкционного материала, когда необходимо иметь высокий уровень свойств во всем объеме, это негативное явление. В нашем случае эффект локализации пластической деформации и уплотнения в верхней части заготовки имеет положительные следствия.
 а
а
|  б
б
|
| Р и с. 7.9. Распределение относительной плотности (а) и твердости HRA (б) по высоте заготовки: 1 – r 10 = 0, 5; 2 – r 10 = 0, 55; 3 – r 10 = 0, 6 |
Напомним, что из заготовок в дальнейшем изготавливаются детали износостойких сопел для пескоструйной обработки и профиль сопла выполняется на плоском участке образующей. С учетом функциональных требований достаточно обеспечить высокий уровень плотности и механических свойств только в верхних ² рабочих² объемах заготовки. Материалы, в которых на основании их функционального назначения целенаправленно создается градиент свойств, получили название функционально-градиентных материалов (ФГМ). В итоге по схеме радиального СВС-прессования получается ФГМ с полезным градиентом плотности по высоте цилиндрических заготовок. Это позволяет, во-первых, уменьшить начальную относительную плотность продуктов синтеза, которая на основании геометрических соотношений для цилиндра круглого сечения принимается равной r 10 = 0, 5 и, во-вторых, вместо шихтовой заготовки в виде цилиндра круглого сечения использовать шихтовую заготовку, имеющую форму сегментного цилиндра. Этот вариант рассматривается ниже в подразд. 7.3. Использование низкоплотных и сегментных шихтовых заготовок обеспечивает снижение материалоемкости изделий.
Таким образом, кинематический анализ показал, что при осевом прессовании однородного порошка в закрытой матрице с криволинейным основанием характер уплотнения прессовки зависит от высоты деформируемого объема. В высоких участках прессовки скорость уплотнения верхних зон больше скорости уплотнения нижних зон. Для низких участков прессовки, наоборот, темп роста плотности нижних зон выше, чем верхних.Этот эффект имеет место и при радиальном СВС-прессовании цилиндрических изделий при передаче давления на заготовку через сыпучую оболочку.
|
|
