Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Крупногабаритных колец

Закономерности уплотнения и формообразования при СВС-прессовании контролируются двумя физическими процессами: теплообменом и пластическим деформированием заготовки и оболочки. Сначала рассмотрим процесс теплообмена, который предшествует процессу деформирования. Для быстрого и равномерного сжигания крупногабаритной шихтовой заготовки используется система многоточечного зажигания [77]. Такой способ зажигания обеспечивает быстрое выравнивание температуры по объему заготовки на стадии синтеза-горения, и можно принять, что в начальный момент времени заготовка мгновенно нагревается до температуры горения Т _г. В этом состоит отличие рассматриваемой задачи от задачи теплообмена при одноточечном зажигании, когда необходимо учитывать подвижность фронта горения и теплообмен за фронтом горения. Температурная задача формулируется следующим образом.

Заготовка в форме кольца толщиной h ₁, внешним радиусом R ₁ и внутренним радиусом r ₁ помещена в сыпучую оболочку и стальную матрицу. Размеры заготовки, оболочки и матрицы известны. В начальный момент времени температура заготовки равна температуре горения Т _г, температура оболочки и инструмента – температуре среды T_S. Требуется найти температурное поле Т (х, t) системы трех соприкасающихся тел в произвольный момент времени t цикла прессования. Здесь х – вектор координат точек системы. Расчетная схема приведена на рис. 6.7. В связи с осевой симметрией рассматривается половина меридионального сечения в цилиндрических координатах r и z.

Математическая постановка задачи осесимметричного теплообмена включает:

1) систему трех дифференциальных уравнений нестационарной теплопроводности в цилиндрических координатах

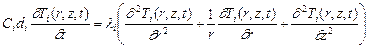, (6.4)

где Т_i – температура тел; С_i – удельная теплоемкость; d_i – гравиметрическая плотность; l_i – коэффициент теплопроводности; t – время; i – индекс тела системы;

2) граничные условия:

на границах «заготовка-оболочка» и «оболочка-инструмент» условия четвертого рода

; T ₁(х, t) = T ₂(х, t);

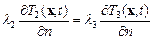; T ₂(х, t) = T ₃(х, t); (6.5)

на границе «инструмент-окружающая среда» условия третьего
рода

+ a _т[ T ₃(х, t) - T_S ] = 0, (6.6)

где a _т – коэффициент теплоотдачи; n – нормаль к граничной поверхности;

3) начальные условия

Т ₁(х, 0) = T _г; Т ₂(х, 0) = T_S; Т ₃(х, 0) = T_S. (6.7)

Здесь, как и ранее, характеристики, относящиеся к заготовке, имеют индекс 1; к оболочке – индекс 2 и к инструменту – индекс 3. Зависимость теплофизических свойств от температуры не учитывалась, и решалась физически линейная задача.

В качестве компактируемого материала рассматривались продукты горения системы Ti-12%(мас.) В. Необходимые для решения задачи теплообмена теплофизические свойства продуктов СВС определялись расчетным путем. Согласно диаграмме состояния продуктом синтеза является твердый сплав состава TiB-40% (мас.) Ti. Температура горения Т _г рассматриваемой системы составляет
Т _г = 1800^оС и превосходит эвтектическую температуру системы Ti-TiB, равную 1667 ^оС [168]. Соответственно продукты синтеза при температуре горения представляют собой двухкомпонентную смесь твердых частиц моноборида титана TiB и боридотитанового расплава, который в свою очередь является двухкомпонентным раствором. Теплофизические свойства смесей рассчитывались по методике, изложенной в п. 2.1. Теплопроводность моноборида титана TiB не исследована, и поэтому использовались справочные данные для диборида титана TiB₂ при температуре 1800 ^оС: = 100 Вт/м× К [4]. Получены следующие значения теплофизических свойств продуктов синтеза: d _СВС = 4, 98 г/см³; l _СВС = 53, 8 Вт/м× К; С _СВС = 873 Дж/кг× К. Эти величины относятся к компактному сплаву TiB-40% Ti. Текущие значения гравиметрической плотности d, коэффициента теплопроводности λ и удельной теплоемкости С уплотняемых продуктов синтеза и песчаной оболочки вычисляли по соотношениям, приведенным в разд. 2. Начальную относительную плотность продуктов синтеза r ₁₀ определяли из условия эквивалентности размеров синтезированной и шихтовой заготовок (см. формулу (2.11)). В экспериментах шихтовая заготовка спрессовывалась до относительной плотности r _ш = 0, 66. При гравиметрической плотности беспористой шихты d _ш = 4, 1 г/см³ и сплава TiB-40% Ti d _СВС = 4, 94 г/см³ расчетное значение начальной относительной плотности составляет r ₁₀ = 0, 55.

Краевая задача пластического деформирования формулируется следующим образом. Горячая пористая заготовка, имеющая форму кольца, помещена в теплоизолирующую песчаную оболочку и в закрытую матрицу. Заготовка является сжимаемым нелинейно-вязким телом; оболочка – сыпучим материалом с хрупкими частицами. Заготовку вместе с оболочкой сжимают жестким пуансоном по заданной ступенчатой программе нагружения. Скорость перемещения пуансона v ₀ на этапе активного нагружения мала, и поле напряжений удовлетворяет условию квазистатичности. На границе заготовки и оболочки выполняется условие полного сцепления по всей поверхности контакта. На границе оболочки с инструментом действуют силы трения. Требуется определить конечные размеры и распределение плотности в материале заготовки и оболочки. Для описания процесса деформирования используется континуальная теория пластического течения сжимаемых сред. Решение сформулированной задачи состоит в нахождении в каждый момент времени t вектора скоростей v (x, t) и относительной плотности r (x, t) точек деформируемой среды. При осесимметричном деформировании поле скоростей определяется двумя компонентами вектора v: осевой скоростью v_z (r, z, t) и радиальной скоростью v_r (r, z, t). Расчетная схема представлена на рис. 6.7.

Математическая формулировка задачи неупругого деформирования включает соотношения Коши, уравнение неразрывности, уравнение равновесия, определяющие соотношения и приведена в подразд. 4.2. Для удобства дальнейшего изложения напомним вид определяющих соотношений для продуктов синтеза

(6.8)

и песчаной оболочки

. (6.9)

К феноменологическим параметрам вязкого течения твердой фазы продуктов синтеза относятся коэффициент А и показатель нелинейности n. Кроме того, коэффициент А определяет температурную зависимость реологических свойств твердой фазы:

, (6.10)

где Т – абсолютная температура; U – энергия активации; k – постоянная Больцмана; С – константа. В определяющих соотношениях песчаной оболочки (6.9) феноменологическим параметром является предел прочности частиц песка t_b. Влияние температуры на прочность частиц песка и расчетная зависимость t_b (Т) были рассмотрены в подразд. 4.1.

Выше уже отмечалось, что при температуре горения сплав TiВ–40% Ti находится в твердожидком состоянии. Напомним основные положения реологической модели пористого вязкого тела с жидкой фазой. В приближении идеальной жидкости сопротивление деформации оказывает только твердая фаза, и параметры a ₁, y и j в уравнениях (6.8) являются функциями объемной доли твердой фазы r_S. Объемная доля твердой фазы r_S связана с относительной плотностью r пористого твердожидкого тела соотношением

r_S = r (1 - m_L). (6.11)

Расчеты показали, что изменение объема расплава m_L при охлаждении сплава TiB-40% Ti от температуры горения до эвтектической температуры можно аппроксимировать следующей линейной зависимостью:

m_L (Т) = 3, 3× 10^-4 Т - 0, 187. (6.12)

В зависимости m_L (Т) температура выражена в градусах Кельвина. При охлаждении сплава ниже эвтектической температуры Т _эвт происходит кристаллизация боридотитанового расплава и жидкая фаза исчезает. Температура Т _эвт является равновесной температурой кристаллизации, и для начала кристаллизации необходима определенная степень переохлаждения. Принималось, что переохлаждение составляет 50^o и при охлаждении от температуры Т _эвт до температуры полной кристаллизации Т _кр объемная доля жидкой фазы изменяется по линейному закону от m_L (Т _эвт) до m_L (Т _кр) = 0. Если объемная доля твердой фазы r_S будет меньше теоретического значения насыпной относительной плотности, составляющей r_{S Н} = 0, 53, то материал заготовки не оказывает сопротивления деформации.

Система разрешающих уравнений пластического деформирования дополняется начальными и граничными условиями. Принималось, что в начальный момент времени относительная плотность по объему заготовки 1 и оболочки 2 распределена однородно:

r ₁(x, 0) = r ₁₀; r ₂(x, 0) = r ₂₀. (6.13)

Рассмотрим граничные условия. На границе «заготовка-оболочка» принималось условие полного сцепления, которое представляет собой равенство скоростей на всей поверхности контакта:
v _к1(x, t) = v _к2(x, t).

На внешней границе оболочки при наличии трения имеют место смешанные граничные условия. Кинематическая часть граничных условий представляет собой условие непроницаемости инструмента (см. рис. 6.7):

v_r (r ₂, z, t) = 0; v_z (r, 0, t) = 0; v_z (r, h, t) = - v ₀; v_r (R ₂, z, t) = 0. (6.14)

Статическая часть граничных условий выражается законом трения на контактной поверхности через соотношение между нормальной s _n и касательной t составляющими вектора поверхностных напряжений. Расчетные зависимости напряжения t для законов трения Кулона и Прандтля приведены в подразд. 4.2.

При ступенчатом нагружении происходит изменение граничных условий на пуансоне. На этапе активного нагружения пуансон перемещается с постоянной скоростью v ₀, и поэтому задавались кинематические граничные условия:

v_z (r, h, t) = - v ₀. (6.15)

На этапе выдержки с постоянным давлением q вместо кинематических граничных условий (6.15) задавались статические граничные условия:

q (r, h, t) = q_j, (6.16)

где q_j – заданное давление прессования на j – том этапе ступенчатого нагружения.

Для описания нелинейно-вязкого течения продуктов синтеза необходимы количественные данные об энергии активации U, константе С и показателе течения n. В литературе этих данных для моноборида титана TiB и материалов на его основе нет. Искомые физические константы были определены следующим образом. Индекс течения n для тугоплавких боридов равен n = 3 [82]. Это значение было принято и для моноборида титана. Энергию активации U находили, опираясь на правило Ле Клера, согласно которому для металлов с одинаковыми типом кристаллической решетки и валентностью отношение энергии активации к температуре плавления Т _пл, выраженной в энергетических единицах kТ _пл, должно быть примерно постоянным [104]. В работе [82] показано, что это правило также выполняется для тугоплавких карбидов и боридов переходных металлов. В частности, для диборида титана TiB₂ отношение U / kT _пл равно значению 23, 9. Из последнего соотношения для температуры плавления моноборида титана Т _пл = 2500 К [168] можно получить величину энергии активации U = 8, 22× 10^-19 Дж. Величину постоянной С в уравнении (6.10) находили с привлечением экспериментальных данных работы [59]. Для модели линейно-вязкого тела коэффициент сдвиговой вязкости m сплава TiB–40% Ti в интервале температур цикла прессования примерно постоянен и равен m = 570 МПа× с [59]. В этой же работе приведены экспериментальные данные по скорости уплотнения dr ₁/ dt для текущей относительной плотности заготовки r ₁, что позволяет из уравнения неразрывности вычислить скорость объемной деформации:

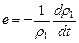. (6.17)

Из определяющих соотношений получим зависимость между скоростью объемной деформации и средним напряжением 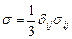для линейно-вязкого (n = 1) и нелинейно – вязкого тел соответственно:

s = 2 myе; (6.18)

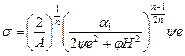. (6.19)

Из условия равенства напряжений (6.18) и (6.19) в характерной точке температурно-временной траектории r ₁(T, t) можно найти искомую величину константы С. В качестве расчетной точки принимались параметры состояния для второго эксперимента в момент начала выдержки при давлении q = 106 МПа. В этот момент времени относительная плотность и скорость уплотнения соответственно равны r ₁ = 0, 92 и dr ₁/ dt = 0, 0364 с^-1. Из решения тепловой задачи получено, что в этот же момент времени средняя по объему температура заготовки составляет Т = 1660 ^оС и сплав содержит жидкую фазу в объеме m_L = 0, 327. Структурные характеристики продуктов синтеза a ₁, y и j рассчитывались по объемной доле твердой фазы r_S, которая согласно (6.11) равна r_S = 0, 616. Данные о сдвиговой вязкости m в работе [59] получены из модели одноосного прессования в жесткой матрице. В этом случае интенсивность скоростей деформации сдвига Н выражается через скорость объемной деформации е: 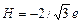. С использованием приведенных соотношений и их количественных оценок определили значение константы С для моноборида титана:
С = 2, 97× 10^-32 м⁷× Н^-2/с.

Поставленная краевая задача пластического деформирования решалась методом конечных элементов. Методика и алгоритм решения краевой задачи изотермического пластического деформирования со смешанными граничными условиями подробно рассмотрены в подразд. 4.2. При неизотермическом процессе в пределах каждого шага решения задачи пластического течения дополнительно выполняется шаг решения задачи нестационарного теплообмена.