Порошковых материалов. Адекватное описание процесса пластического или вязкого деформирования порошковых тел возможно при условии точного определения феноменологических параметров и

Адекватное описание процесса пластического или вязкого деформирования порошковых тел возможно при условии точного определения феноменологических параметров и их зависимостей от пористости. Функции пористости y, j в уравнении (1.1) представляют собой соответственно отношение модуля всестороннего сжатия и модуля сдвига пористого тела к модулю сдвига несжимаемой твердой фазы. Из аналогии между теорией упругости и гидродинамикой линейно-вязкой среды следует идентичность функциональных зависимостей y (q) и j (q) для пластического и вязкого пористого тела в определяющих соотношениях (1.3).

Зависимости y (q) и j (q) для эллиптических условий пластичности определялись как экспериментально [93, 105, 142, 154, 179, 245, 255, 260, 263, 273, 279], так и теоретически [29, 30, 34, 36, 46, 88, 153, 170, 185, 190, 258, 260, 272]. Некоторые аналитические аппроксимации функций y и j приведены в работе [231]. Теоретические зависимости находились из решений модельных задач поведения представительного элемента пористого тела при двух различных напряженных состояниях. В условиях чистого сдвига определялся вид функции j (q); в условиях гидростатического нагружения – вид функции y (q). В теоретических моделях в качестве представительного элемента пористого тела использовались полый шар [29, 34, 36, 199, 260], полый куб [170, 272], полый цилиндр [34, 36, 258], брус квадратного сечения с цилиндрическим отверстием [88], цилиндр со сферической полостью [30] и статистические смеси вещества и пустоты [16, 46, 185, 190].

Для коэффициентов вязкости непосредственно принимаются зависимости, которые установлены для модулей упругости пористых тел. На основании экспериментальных данных предложены степенные зависимости модуля Юнга и коэффициента Пуассона пористого тела от пористости [9, 55, 75, 81, 218]. Теоретический подход основан на использовании методов расчета эффективных упругих свойств двухфазных матричных композитов с включениями. В соотношениях для композитов включения наделяют нулевыми материальными константами и получают искомые зависимости для пористых тел. В настоящее время разработан ряд теоретических методов расчета упругих постоянных микронеоднородных тел [23, 89, 110, 120, 149, 169, 172, 178, 224, 225, 229]. Однако для несплошных тел представляют интерес лишь такие методы, которые рассматривают материалы с существенно различными свойствами компонентов [83]. Это вариационный метод Хашина-Штрикмана и метод самосогласования, основанный на принципе эквивалентного включения Эшелби [237]. Вариационный метод дает очень широкую вилку отношений эффективных упругих модулей пористого тела к соответствующим модулям твердой фазы [83]. Метод самосогласования не в состоянии описать поведение материалов с большой объемной долей пор [184, 241, 257]. Кроме того, различные исходные структурные модели дают отличающиеся друг от друга результаты [229].

Выше уже отмечалось, что поровая структура реальных квазисплошных тел намного сложнее, чем принимается в теоретических моделях, и теория может дать только приближенный результат. В работе [154] показано, что из-за различия поровой структуры не существует единых зависимостей для экспериментальных функций пористости. Соответственно не могут быть установлены и единые теоретические зависимости для всех разновидностей несплошных тел. Для точных моделей предлагается определять вид функций пористости для каждого материала экспериментально [142, 154]. Такой подход может быть осуществлен для однопараметрических моделей, когда известны или могут быть установлены реологические свойства беспористой твердой фазы. Для материалов, у которых температура плавления позволяет получить образцы в беспористом состоянии, искомые реологические свойства могут быть напрямую определены из соответствующих экспериментов. Тугоплавкие соединения, имеющие температуру плавления свыше 2500 ^оС, получают, как правило, в порошкообразном состоянии. Материалы теплоизолирующей оболочки, например песок, в исходном состоянии также являются дисперсным телом. Беспористые образцы из природно-порошкообразных материалов будут содержать ² биографические² макродефекты, связанные с технологическими условиями изготовления образцов из порошков. Естественно, что свойства компактного материала, состоящего из частиц, подвергнутых различным технологическим воздействиям, будут значительно отличаться от свойств исходных дисперсных частиц. Более точный результат (и без дополнительных затрат на компактирование) может быть получен при проведении экспериментов для исходного дисперсного состояния материала. При обработке экспериментальных результатов необходимо выделить эффекты, которые вызваны пористостью. Прямой путь экспериментального определения функциональных зависимостей коэффициентов сдвиговой и объемной вязкости от пористости требует проведения большого числа испытаний по схемам высокотемпературного сдвигового или объемного деформирования. В этой связи на практике реализуется подход, при котором априори принимаются определенные теоретические зависимости функций пористости и феноменологические константы находят из относительно простых опытов, например, при одноосном сжатии в закрытой матрице [82]. Получаемые таким образом оценки эффективных реологических свойств вещества твердой фазы жестко связаны с принятыми функциями пористости. Наибольшее распространение и достаточно хорошее соответствие с экспериментальными данными [115] имеют зависимости, полученные В.В. Скороходом методом самосогласования [184]. Для принятых формулировок эллиптического условия пластичности (1.1) и определяющих соотношений (1.3) эти функции имеют следующий вид:

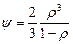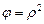; . (1.4)

Имеющиеся экспериментальные данные об эффективных реологических свойствах тугоплавких соединений [82] получены для зависимостей, отличающихся от соотношений (1.4) только постоянным множителем, поэтому в настоящей работе при построении реологических моделей продуктов синтеза и сыпучей оболочки авторы используют функции y и j в виде (1.4).

В континуальной теории деформируемое порошковое тело рассматривается как двухфазный материал, состоящий из пластичной или вязкой твердой фазы и порового пространства. Вместе с тем горячие продукты СВС при температуре деформирования, как правило, содержат жидкую фазу в виде расплава легкоплавких компонентов [58, 148, 215]. В работе [199] исследовано влияние жидкой фазы на реологические свойства пористых тел с пластической твердой фазой, однако влияние жидкой фазы на реологические свойства пористых тел с вязким веществом в научной литературе не рассматривалось.