Материалов

Необходимым условием получения беспористых изделий является способность синтезированного материала к пластическому деформированию. Тугоплавкие соединения, которые являются основой СВС-прессованных материалов, начинают проявлять макропластические свойства при гомологических температурах выше (0, 5¸ 0, 7) Т _пл [4]. Технологически необходимый уровень пластичности приобретается при температурах выше температуры рекристаллизации, и по температурному режиму процессы обработки давлением тугоплавких соединений относятся к процессам горячей деформации. Как показывают эксперименты [82], горячая деформация тугоплавких соединений осуществляется по механизму вязкого течения. Выше уже отмечалось, что в СВС-материалах тугоплавкие соединения образуются в виде дисперсных частиц [215, 265] и они по своей структуре идентичны порошкам, но с вязкой твердой фазой. Известно, что вязкая среда прилипает к граничным поверхностям [109], поэтому в дисперсно-вязких телах межчастичного скольжения нет и деформирование связано только с вязким течением твердой фазы в поры согласно теории Я.И. Френкеля. Аналогичная реологическая модель горячих продуктов синтеза используется для описания процесса СВС-экструзии [17, 191, 195].

Горячее прессование порошковых материалов рассматривается как разновидность спекания при постоянном давлении [82], и теория горячего деформирования порошковых тел развивалась параллельно с теорией спекания. Ранние теории спекания основывались на представлениях о дискретном характере порошковых тел. Основные этапы развития и результаты дискретной теории спекания, в том числе по механизму вязкого течения, подробно рассмотрены в работах [24, 82, 181, 187]. Имея исключительно большое значение для изучения физического механизма межчастичного взаимодействия, это направление, как и дискретно-контактные теории пластического деформирования, не позволяет учесть такие макроскопические факторы, как кинематические граничные условия, внешнее механическое воздействие, форму тела и др.

Основы континуального подхода к описанию процесса спекания и горячего деформирования были сформулированы в работах Дж. Маккензи [266, 267], где впервые была обоснована аналогия между гидродинамикой линейно-вязкой среды и теорией упругости. С макроскопической точки зрения пористое тело рассматривается как сжимаемая среда с двумя коэффициентами вязкости – сдвиговой и объемной. При этом предполагается, что вязкий и упругий тензоры напряжений имеют одинаковую структуру, если и упругое тело, и линейно-вязкая жидкость являются изотропными. Тензору деформации в теории упругости соответствует тензор скорости деформаций в теории вязкого течения, модулю сдвига соответствует коэффициент сдвиговой вязкости, а модулю всестороннего сжатия – коэффициент объемной вязкости.

Дальнейшее развитие континуальной модели спекания связано с работами В.В. Скорохода [182-184], рассмотревшего пористое тело как предельный случай композиционного материала, в котором одна из фаз имеет нулевые материальные константы. Особенно эффективным оказалось применение метода диссипативной функции к описанию поведения пористых тел [183, 184]. Метод диссипативной функции позволил достаточно просто получить аналитические решения для ряда модельных задач об однородном деформировании линейно-вязких пористых тел [184]. На основании постулата об однозначности диссипативной функции пористого тела и его вещества появилась возможность оценить уровень истинных напряжений и истинных скоростей деформации в вещественной фазе несплошного тела [82, 183, 184]. Это позволило выполнить обобщение теории на случай нелинейного течения твердой фазы, образующей пористое тело [37, 286]. В основу обобщения положена уже упоминавшаяся ранее гипотеза [186, 231, 232]: зависимость эквивалентной скорости деформации твердой фазы от макроскопических скоростей деформаций инвариантна относительно реологических свойств твердой фазы. Для линейно-вязкого тела эквивалентная скорость деформации твердой фазы w равна [186, 188]

, (1.2)

где е – макроскопическая скорость объемной деформации; g – макроскопическая скорость изменения формы. Принимается, что зависимость (1.2) имеет место для нелинейно-вязкой или пластической твердой фазы.

Из макроскопического диссипативного потенциала и принципа Онзагера для необратимых деформаций следуют определяющие соотношения между тензором напряжений s_ij и тензором скоростей деформаций е_ij для пористого тела с произвольной реологией твердой фазы [186, 188]:

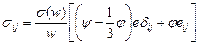, (1.3)

где s (w) – эквивалентное напряжение в твердой фазе, функционально связанное с эквивалентной скоростью деформации w; dij – символ Кронекера.

Статистическое осреднение микроскопических скоростей деформации сдвига в работах [186, 188] проводится по всему объему вещества, количественной мерой которого в зависимости (1.2) служит относительная плотность r пористого тела. Осреднение по всему объему вещества несплошного тела означает, что независимо от вида макроскопической деформации все вещество испытывает однородную деформацию растяжения-сжатия или сдвига [82, 184]. Вместе с тем известно, что пористые и порошковые тела деформируются неоднородно, и пластическая деформация локализуется вокруг пор в пористых материалах или в зонах контакта частиц в порошках [9, 13, 55, 70, 116]. Это явление, по-видимому, должно иметь место и для дисперсно-вязких тел. Условия пластичности, учитывающие локализацию пластической деформации вокруг пор в пористых телах, рассмотрены в работах [36, 199]. Для континуальных моделей пластических и вязких порошковых материалов этот вопрос в научной литературе не рассматривался.

В дискретно-контактных теориях [9, 55] неоднородный характер пластической деформации частиц учитывается тем, что поля напряжений и пластических деформаций связывают не с полным объемом твердой фазы, а лишь с ее частью – активным объемом [9]. Активный объем представляет собой объем, прилегающий к контактным поверхностям частиц. Уравнения прессования, использующие концепцию контактного объема, достаточно хорошо соответствуют экспериментальным данным [2, 9, 55]. В этой связи перспективным представляется развитие континуальной теории пластического и вязкого течения порошковых тел на основе структурных моделей дискретно-контактной теории.