Порошковых материалов. Ранние теоретические работы по деформированию и уплотнению порошковых материалов основывались на анализе условий контактного взаимодействия и деформаций

Ранние теоретические работы по деформированию и уплотнению порошковых материалов основывались на анализе условий контактного взаимодействия и деформаций отдельных частиц и отражали дискретное строение порошков. Основой дискретно-контактных теорий являются уравнения, моделирующие процесс прессования, в котором функционально связаны плотность прессовки и приложенное давление. В соответствующие формулы включены некоторые параметры, подлежащие определению опытным путем, как правило, при одноосном прессовании в закрытой матрице. Оценка состояния дискретно-контактного направления дана в монографиях [5, 55, 71, 151]. В рамках дискретно - контактного подхода оказывается невозможным учет взаимодействия прессовки с инструментом, поэтому не поддаются учету такие факторы, как схема деформирования, кинематические граничные условия, влияние внешнего трения, течение порошка в радиальном направлении и др. [173].

В настоящее время доминирующей является континуальная теория пластического деформирования уплотняемых тел, в соответствии с которой порошковое тело рассматривается как сплошная среда. Континуальный подход для несплошных сред основывается на концепции представительного элемента [43, 214, 230]. Согласно этой концепции точка континуума отождествляется с областью, размеры которой малы по сравнению с размерами образца, но велики по сравнению с отдельными частицами. Свойства представительного элемента полагаются идентичными свойствам тела. Для каждого элемента и материала в целом выполняются все основные законы механики и термодинамики континуума. О допустимости континуального подхода свидетельствуют экспериментальные данные с использованием крашенных порошков [158], которые показывают, что при прессовании в закрытых пресс-формах происходит депланация поперечного сечения с сохранением целостности слоев порошка.

Континуальная теория пластического и вязкого течения несплошных сред получила развитие в работах С.Е. Александрова, В.Н. Анциферова, Я.Е. Бейгельзимера, А.К. Григорьева, Г.Я. Гуна, И.С. Дегтярева, Б.Н. Дидуха, Е.А. Дорошкевича, Б.А. Друянова, В.В. Дудукаленко, В.Т. Головчана, А.Г. Залазинского, Л.А. Исаевича, В.П. Каташинского, О.А. Катруса, С.Л. Киселева, В.Л. Колмогорова, А.М. Лаптева, Е.Б. Ложечникова, В.З. Мидукова, И.Ф. Мартыновой, Н.Н. Павлова, В.Е. Перельмана, Г.Л. Петросяна, И.Д. Радомысельского, О.В. Романа, А.И. Рудского, В.Д. Рудь, В.М. Сегала, А.Н. Смыслова, А.В. Степаненко, В.В. Скорохода, М.Б. Штерна, В.Н. Цеменко и многих других ученых.

Среди зарубежных ученых большой вклад в развитие теории пластичности сжимаемых тел внесли Д. Вилкинсон, Р.Дж. Грин, А. Гэрсон, К. Дауни, Д. Друккер, Х. Кун, Дж. Маккензи, М. Ояне, В. Прагер, Н.Р. Сах, Т. Табата, В. Твергаард, Р. Хилл, Р.Т. Шилд, С. Шима, М. Эшби и др.

Основная проблема математического моделирования процесса пластического деформирования связана с выбором определяющих соотношений. По аналогии с теорией пластичности несжимаемых материалов определяющие соотношения для сжимаемых сред могут быть построены в рамках деформационной теории и теории пластического течения.

Теоретические и прикладные вопросы деформационной теории сжимаемых тел изложены в работах [95, 96, 142, 143]. Определяющие уравнения деформационной теории относительно просты и удобны для расчета напряженно-деформированного состояния, однако область их применения ограничена малыми упруго-пластическими деформациями и случаями простого (или близкого к простому) нагружения [95, 96]. Решения задач деформирования жесткопластического пористого материала по деформационной теории и теории течения совпадают только в случае простого нагружения в девиаторной плоскости и при гидростатическом нагружении [95]. Большинство технологических процессов деформирования порошковых материалов не удовлетворяет этим условиям, и деформационная теория не нашла широкого применения для рассматриваемого круга задач.

В теории пластического течения определяющие соотношения могут быть получены двумя эквивалентными путями: либо через определение функции нагружения (условия пластичности), либо через определение диссипативной функции [18, 66]. Качественные особенности теорий пластичности удобно рассматривать при ана­лизе формы поверхности нагружения, которую в пространстве на­пряжений определяет функция нагружения. Наглядное представле­ние об условии текучести можно получить, представляя поверх­ность нагружения в пространстве главных напряжений s ₁, s ₂, s ₃ или кривую нагружения на плоскости р - Т, где р – гидростатическое давление; Т –интенсивность касательных напряжений. Если опреде­ляющие соотношения получены из диссипативного потенциала, то и в этом случае восстанавливают функцию нагружения и соответст­вующую ей поверхность нагружения.

По основной гипотезе теории течения функцию нагружения отождествляют с пластическим потенциалом для скоростей пласти­ческих деформаций и из ассоциированного закона находят искомые определяющие соотношения. Ассоциированный закон течения сле­дует из постулата Д. Друккера, согласно которому работа на замк­нутом по напряжениям цикле нагружения неотрицательна. Другое следствие постулата Д. Друккера состоит в том, что вектор скоро­сти пластической деформации направлен по нормали к поверхности или кривой нагружения в той ее точке, которая соответствует действительным напряжениям. Экспериментальные исследования [67, 121] показали, что для реальных процессов деформирования порошковых материалов векторы скоростей пластической деформации ортогональны к поверхности нагружения и для этих материалов также выполняется ассоциированный закон.

Условие пластичности формулируется путем комбинаций инвариантов тензора напряжений. Неоднократно было установлено [219], что учет третьего инварианта тензора напряжений в теории пластичности несжимаемых тел не дает существенных количественных уточнений. Аналогичный результат получен авторами работы [233], рассмотревшим влияние третьего инварианта на пластичность пористых тел. Полученные в [233] определяющие соотношения содержат выражения, которые сводятся к эллиптическим интегралам и не могут быть выражены через элементарные функции, поэтому современные теории пластичности сжимаемых тел учитывают только первый и второй инварианты тензора напряжений. Так как рассматриваются условия пластичности, которые не зависят от третьего инварианта тензора напряжений, то ось поверхности нагружения совпадает с гидростатической осью. Условие пластичности несжимаемых материалов не зависит также от среднего напряжения, и поверхность нагружения не замкнута. Она представляет собой либо цилиндр Мизеса, либо призму Треска с образующей, параллельной октаэдрической оси. Пластическое уплотнение при гидростатическом нагружении, свойственное порошковым материалам, может быть описано в рамках моделей, использующих лишь замкнутую поверхность нагружения.

Физически адекватные модели должны отражать следующие основные закономерности пластического течения порошковых материалов:

1) эффект изменения объема при сдвиге (эффект пластической дилатансии);

2) разносопротивляемость порошковых материалов растяжению и сжатию (деформационная анизотропия);

3) двойственный механизм необратимой деформации – межчастичное скольжение или пластическое деформирование частиц.

Важным свойством модели пластического тела является возможность получения однозначной зависимости компонентов тензора напряжений от скоростей деформаций. Это позволяет формулировать задачу в кинематических переменных и использовать для решения вариационные и основанные на них численные методы. Свойством однозначности определяющих соотношений обладают только строго выпуклые поверхности нагружения [44]. С учетом отмеченных требований рассмотрим известные континуальные модели пластического течения порошковых материалов.

Такие свойства дисперсных материалов, как явление дилатансии и значительные изменения объема при пластической деформации, впервые установлены для грунтов. Именно в механике грунтов в 60-х гг. прошлого столетия были предложены многочисленные критерии пластичности, зависящие от гидростатического давления [38, 39, 128, 246-248, 261, 280, 281]. Подробный анализ этих критериев был выполнен Н.Н. Николаевским в работе [127]. Несколько позднее были предложены еще две модели дилатирующих материалов.

В.В. Дудукаленко и А.Ю. Смыслов [45] на основе статистической модели условия текучести Мизеса-Шлейхера получили поверхность нагружения, которая на плоскости р - Т описывает область, ограниченную сбоку отрезками эллиптических кривых и имеющую плоское дно, которое расположено перпендикулярно оси гидростатического сжатия. Авторы отмечают, что форма теоретической области предельного равновесия близка к экспериментально определенной в [38] форме области предельного равновесия.

Э.С. Макаров [112, 113] для обеспечения гибкости при описании процесса деформирования порошковых материалов предложил использовать многопараметрические поверхности нагружения. Эти поверхности нагружения не имеют физического обоснования и представляют собой аналитическую аппроксимацию экспериментальных данных. Для определения эмпирических параметров и их зависимостей от плотности необходимо проводить многочисленные эксперименты по схемам, труднореализуемым для порошковых тел – одноосное растяжение и сжатие, а также кручение.

Рассмотренные критерии пластичности [38, 39, 45, 112, 113, 127, 128, 246 – 248, 261, 280, 281], основанные на условии Кулона-Мора, ориентируются, главным образом, на описание дилатансии грунтов, а не на уплотнение, которое характерно для процессов технологического деформирования порошков [278]. Кроме того, требуются трудоемкие экспериментальные процедуры для построения поверхностей нагружения и определения феноменологических параметров и их зависимостей от плотности.

В ранних работах для описания процесса деформирования порошковых тел использовались условия пластичности и соответствующие им поверхности нагружения, которые во многом подобны применяемым в механике грунтов.

Для анализа качественной картины пластического течения используется упрощенное условие текучести, которому соответствует поверхность нагружения в виде кругового цилиндра с двумя плоскими донышками. Эта модель впервые предложена С.С. Григоряном в механике грунтов [32, 33]. При цилиндрическом условии пластичности дилатансионное соотношение отсутствует, и соответствующая модель характеризуется независимыми механизмами сдвига и уплотнения [44]. Достоинства и недостатки этой модели подробно рассмотрены в работе [214].

В модели В.Е. Перельмана [5, 139, 140] использовались обобщенный закон Кулона-Мора и поверхность нагружения в виде правильной шестиугольной пирамиды с плоским дном, пересекающим гидростатическую ось в области сжимающих напряжений. Интенсивность уплотнения, функционально связанная с давлением и степенью деформации, принималась зависящей не от пористости, а от угла внутреннего трения. Применение ассоциированного закона течения к этой модели не представляется возможным [140].

Т. Табата, С. Масаки, Ю. Абе [282] предложили критерий пластичности, подобный критерию В.Е. Перельмана. Вместе с тем они учли влияние на вид критерия пластичности знака среднего напряжения. Соответствующая поверхность нагружения представляет собой две правильные пирамиды с общим основанием. Высоты пирамид совпадают с гидростатической осью; координаты вершин по модулю равны пределам текучести на гидростатическое сжатие или гидростатическое растяжение. Недостатки пирамидального и подобных ему условий пластичности, использующих условие Треска, отмечены в работе [97]. Во-первых, при расчетах необходимо заранее знать, какое из трех главных напряжений наибольшее, а какое наименьшее, что не всегда можно установить. Во-вторых, эти критерии не учитывают влияния промежуточного главного напряжения на процесс пластического деформирования.

Недостатков пирамидального условия пластичности не имеет условие пластичности, предложенное в работе [282]. Этому условию пластичности, являющемуся обобщением критерия Друккера-Прагера [248], в пространстве главных напряжений соответствует поверхность нагружения в виде двух конусов, опирающихся на девиаторную плоскость общим основанием. Высоты конусов совпадают с гидростатической осью; координаты вершин по модулю равны пределам текучести на гидростатическое сжатие или гидростатическое растяжение. Различие в высоте конусов или пирамид может отражать разное сопротивление пористого материала растяжению и сжатию.

Важным этапом в развитии теории пластического деформирования квазисплошных тел явилось создание моделей, в которых поверхность нагружения принимается в виде эллипсоида вращения, симметричного относительно оси гидростатического давления и девиаторной плоскости. Размеры полуосей эллипсоида являются функциями объемной концентрации пор. Сечение эллипсоида плоскостью р - Т представляет собой эллипс, и эллипсоидальное условие чаще называют эллиптическим. Эллиптическое условие является строго выпуклым и обеспечивает однозначную зависимость компонентов тензора напряжений от скоростей деформаций. Появлению эллиптического условия пластичности способствовало развитие методов обработки давлением не полностью спеченных материалов с остаточной пористостью, которые образовали класс новых объектов – пористых тел [214]. Было установлено, что с макроскопической точки зрения при уплотнении в замкнутых объемах поведение пористых тел подобно поведению порошков [114, 145], а при наличии свободной поверхности они так же, как и компактные тела, могут деформироваться без разрушения. Первоначальный вариант эллиптического условия пластичности, предложенный Г. Куном и Ч. Дауни [263], основывался на экспериментальных данных. В настоящее время эллиптическое условие пластичности получило многочисленное экспериментальное и теоретическое обоснование [1, 16, 29, 30, 31, 34, 36, 46, 88, 93, 105, 122, 153, 154, 167, 170, 179, 185, 190, 199, 244, 245, 252, 254, 255, 258, 260, 272, 273, 275, 279, 284] и наиболее широко используется при решении прикладных и технологических задач обработки давлением порошковых и пористых материалов.

Многочисленные математические формулировки эллиптического условия пластичности связаны с использованием разными авторами различных структурных моделей и методов решения задачи о пластическом равновесии пористых тел. Основное различие связано с разным типом функций, определяющих зависимость свойств материала от пористости. Однако поровая структура реальных квазисплошных тел намного сложнее, чем принимается в теоретических моделях. Прежде всего, следует отметить неправильную форму пор, различие размеров, степень разветвленности и связности и т.д. Существенное влияние на механические свойства оказывают также технологические факторы (способ получения порошкового или пористого материала, режимы термообработки и др. [9, 55, 180]), поэтому теоретическое описание свойств несплошных материалов может дать только приближенный результат. Точность теории может быть обеспечена путем экспериментального определения феноменологических параметров в моделях относительно простой математической формы. Соответственно в дальнейшем рассматриваются эллиптические условия пластичности, полученные при предельном переходе изотропного представительного элемента к пластическому состоянию из упругой или вязкой области. Предельный переход из упругой области основан на гипотезе Бельтрами и ее обобщениях [153, 185, 199, 214]. Переход из линейно-вязкой области осуществляется на основании гипотезы о том, что зависимость осредненной интенсивности скоростей деформации сдвига твердой фазы от макроскопических скоростей деформаций инвариантна относительно реологических свойств твердой фазы [186, 231, 232].

В физической формулировке эллиптический критерий пластичности идентичен условию пластичности Бельтрами: пластическое течение наступает тогда, когда сумма удельных упругих энергий изменения формы и объема достигает предельного значения для данного материала. Соответствующая математическая формулировка имеет вид [186, 230]

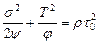, (1.1)

где y, j – функции пористости q или относительной плотности r, которая связана с соотношением r = 1 - q; s – среднее напряжение; Т – интенсивность касательных напряжений сдвига; t ₀ – предельное напряжение сдвига, равное пределу текучести на сдвиг пластичной твердой фазы или пределу прочности при сдвиге хрупкой твердой фазы. За предельное значение суммарной упругой энергии принимается предельное значение удельной упругой энергии изменения формы несжимаемой твердой фазы, количественной мерой которой служит относительная плотность r. Функции y и j выбираются так, чтобы обеспечить предельные переходы 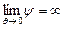; 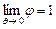. Тогда для беспористого материала эллиптический критерий (1.1) переходит в критерий пластичности Мизеса.

Отметим, что в работах [186, 230] интенсивность касательных напряжений сдвига через компоненты тензора-девиатора напряжений s_ij определена выражением . В настоящей работе рассматривается классическое понятие интенсивности касательных напряжений сдвига . Это различие приводит к появлению множителя 2 в знаменателе перед y.

Эллиптическое условие пластичности, первоначально разработанное для описания механического поведения пористых тел, можно применять и для порошковых материалов, деформируемых в замкнутых объемах с преобладанием сжимающих гидростатических давлений [115, 231]. В этом случае экспериментально определенная область предельного равновесия имеет форму эллипса [67, 122, 154, 167]. Однако опытные данные о поведении порошковых материалов при трехосном нагружении [154, 193, 285] показывают, что в области малых степеней связности и при малых значениях гидростатического давления наблюдается существенное отклонение от эллиптического условия пластичности. Это расхождение следует связать с изменением механизма деформирования порошкового материала – вместо пластической деформации частиц происходит межчастичное скольжение (структурная деформация).

Обобщение концепции предельного перехода представительного элемента от упругого состояния к пластическому для случая структурной деформации выполнено в работе [12]. Здесь предполагается, что в твердой фазе имеет место внутреннее трение и предельное напряжение сдвига t ₀ в (1.1) является функцией гидростатического давления р и подчиняется закону сухого трения Кулона. При определенном значении гидростатического давления р * величина напряжения сдвига твердой фазы становится равной своему предельному значению – пределу текучести для пластичных частиц или пределу прочности для хрупких частиц. Начиная с величины р * скольжение частиц прекращается и порошковый материал деформируется за счет пластического сдвига или разрушения частиц. Указанное обобщение приводит к асимметричному расположению поверхности нагружения относительно девиаторной плоскости и учету деформационной анизотропии порошкового тела. При деформировании по механизму скольжения в зависимости от плотности порошка поверхность нагружения может быть эллипсоидом, параболоидом или гиперболоидом вращения.

Эллиптическое условие пластичности порошкового тела с пределом текучести, подчиняющимся закону трения Кулона, предложено также в работе [278]. Авторы этой работы не проводили анализ влияния плотности порошка на форму поверхности нагружения и считают, что учет внутреннего трения приводит только к сдвигу эллипсоидов вдоль гидростатической оси в сторону сжимающих давлений. Кроме того, не введено ограничение по величине гидростатического давления, при котором прекращается межчастичное скольжение и наступает пластический сдвиг частиц. Несмотря на отмеченные недостатки, за счет феноменологических параметров получено хорошее соответствие результатов расчета и эксперимента при одноосном сжатии образцов из неспеченного медного порошка.

Дисперсное состояние порошковых тел, наряду с двойственным механизмом пластического деформирования, обусловливает принципиально разное механическое поведение порошка и пористого тела в начальном состоянии. Пористое тело с непрерывной матричной структурой твердой фазы оказывает сопротивление деформации при любой величине плотности, в том числе и начальной. В отличие от пористых тел пластическая деформация порошков в состоянии насыпной плотности, когда r = r ₀, начинается при произвольно малых нагрузках. Вместе с тем из (1.1) следует, что для состояния насыпной плотности сопротивление порошка чистому сдвигу Т отлично от нуля: . Следовательно, структурная модель с осреднением локальных напряжений и скоростей деформаций по всему объему вещества не удовлетворяет граничным условиям по напряжениям для насыпного состояния порошкового тела. Этот недостаток также характерен для моделей [12, 278]. В работах [35, 72] отсутствие сопротивления деформации порошков при насыпной плотности r₀ учитывается через функции пористости y, j. В этом случае проводят нормировку функций y и j: вместо относительной плотности r используется параметр вида 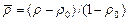, который принимает нулевое значение при r=r ₀. При этом нормируются либо один [72], либо все аргументы r [35], входящие в функции y и j. Такой подход носит формально-математический характер и не имеет физического обоснования.

Обобщение для несплошных тел модели микронеоднородного континуума и таких фундаментальных физических свойств, как энергия и диссипация энергии пластической деформации, приводит к получению поверхностей нагружения второго порядка. В работах [193, 194] в рамках формального выполнения требований к замкнутости и строгой выпуклости предложена поверхность нагружения четвертого порядка в пространстве главных напряжений. Благодаря своей структуре критерий пластичности [193, 194] обладает достаточной общностью; его можно распространить как на пористые, так и на порошковые тела. В последнем случае обеспечивается выполнение граничных условий по напряжениям при насыпной плотности. В качестве частных случаев из рассматриваемого критерия следуют поверхности нагружения в форме лемнискаты вращения [281], цилиндра с плоскими донышками и эллипсоида вращения. Однако универсальность достигается за счет использования большого числа экспериментальных констант и функций, которые определяются в технически сложных для порошковых материалов экспериментах – гидростатическое сжатие и растяжение, а также кручение. В итоге определяющие соотношения имеют громоздкий вид и неудобны для практического применения.

Физически строгие континуальные модели порошковых тел должны отражать, во-первых, дискретно-контактное строение порошков и, во-вторых, двойственный механизм пластической деформации (межчастичное скольжение или пластический сдвиг частиц). В известных эллиптических условиях пластичности [12, 278] учитывается только двойственный механизм пластической деформации. Многопараметрическое условие пластичности [193, 194] отражает обе особенности порошковых тел, однако формально-математический подход обуславливает необходимость проведения многочисленных трудоемких экспериментов. Таким образом, в настоящее время отсутствуют физически обоснованные и достаточно простые условия пластичности, в которых одновременно учитываются и механизм деформации, и несвязанное начальное состояние порошковых материалов.