
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: Деление двоичных знаковых чисел в компьютерных системах
|
|
Так как данные в памяти компьютера хранятся в ДК, операцию деления целесообразно выполнять в ДК.
За основу можно принять базовый алгоритм деления (без восстановления остатка), т.к. он предполагает использование отрицательного делителя, дополнительного кода для вычитания и учет знаков остатка и делителя на каждом шаге деления.
Делимое участвует в операции только на первом шаге, а далее используются остатки, которые могут быть как положительными, так и отрицательными. Поэтому не имеет смысла рассматривать алгоритмы деления в ДК, где знаки операндов обрабатываются отдельно от их числовых частей.
Таким образом, при делении чисел в ДК трудности, связанные с коррекцией результата (как при умножении в дополнительном коде), практически отсутствуют.
Пусть:
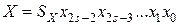 - разрядность (2s), -
- разрядность (2s), - 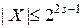 .
.
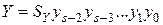 - разрядность (s), -
- разрядность (s), - 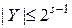 .
.
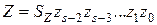 - разрядность (s), -
- разрядность (s), - 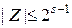 .
.
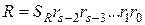 - разрядность(s), -
- разрядность(s), - 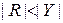 .
.
Для проверки на корректность операции деления используется условие:
 . Таким образом, при пробном вычитании делитель должен быть сдвинут на (s-1) разряд влево. Однако чтобы обеспечить регулярность процесса деления, делитель сдвигается влево на s разрядов, а перед пробным вычитанием делимое сдвигается на один разряд влево.
. Таким образом, при пробном вычитании делитель должен быть сдвинут на (s-1) разряд влево. Однако чтобы обеспечить регулярность процесса деления, делитель сдвигается влево на s разрядов, а перед пробным вычитанием делимое сдвигается на один разряд влево.
В каждом цикле сдвинутый остаток складывается с делителем, которому приписывается знак, противоположный знаку частичного остатка.
Алгоритм деления знаковых чисел отличается от алгоритма деления беззнаковых чисел способом формирования разрядных цифр частного.
Очередная цифра определяется на основе анализа знаков частичного остатка и делителя. Если знак полученного остатка совпадает со знаком делителя, то цифра частного равна (1), если нет – (0). При этом частное формируется в прямом или обратном коде (в зависимости от соотношения знаков делимого и делителя). На этапе пробного вычитания автоматически формируется старшая цифра частного, которая представляет его знак. Если знак полученного частичного остатка совпадает со знаком делителя, участвующего в операции пробного вычитания, деление является корректным. В противном случае имеет место переполнение разрядной сетки компьютерной системы.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Алгоритм деления целых двоичных знаковых чисел заключается в следующем:
1. Частному присваивается значение (0); (Сч.Т) – (s). Исходное значение частичного остатка равно (s) старшим разрядам делимого.
2. Частичный остаток удваивается сдвигом влево на (1) разряд, с занесением в младший разряд очередной цифры делимого.
3. Если частичный остаток и делитель разного знака, то они складываются, если же одного знака, то из частичного остатка вычитается делитель.
4. Частное сдвигается влево на (1) разряд. В освобождающийся младший разряд заносится очередная цифра частного: (1) - если знак делителя и остатка совпадают, (0) - в противном случае (Сч.Т) уменьшается на (1).
5. Пункты 2-4 повторяются до тех пор, пока (Сч.Т) не станет равным (0).
6. Частное и остаток сформированы в обратном коде. Если знак окончательного остатка не совпадает со знаком делимого, то выполняется его восстановление. Для получения ДК результата выполняется его коррекция в зависимости от соотношения знаков делимого и делителя.
При делении в дополнительном коде возможные комбинации знаков операндов образуют следующий перечень.
Случай №1 X > 0; Y > 0. Деление в этом случае ничем не отличается от деления положительных операндов в прямом коде. Коррекция не требуется;
Случай №2 X > 0; Y < 0. Этот случай легко сводится к обычному делению в прямом коде, если считать, что в наличии имеется (-Y) и (+Y). Однако для формирования правильного знака частного и обратного кода отрицательного результата необходимо псевдознаковую цифру и цифры частного получать равными цифрам знаковых разрядов соответствующих остатков. Переполнение разрядной сетки здесь фиксируется по (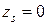 ). В конце деления для образования дополнительного кода и округления частного следует прибавить единицу к младшему разряду: (Z=Z’+1);
). В конце деления для образования дополнительного кода и округления частного следует прибавить единицу к младшему разряду: (Z=Z’+1);
Случай №3 X < 0; Y > 0. Из отрицательного делимого должен вычитаться положительный делитель, в отличие от деления без восстановления остатка в прямом коде, когда на первом шаге (Х> 0, Y< 0). Поэтому псевдознаковая цифра частного (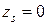 ), полученная по знаку нулевого остатка в соответствии с алгоритмом деления без восстановления остатка, здесь указывает на переполнение разрядной сетки. Если же переполнения разрядной сетки нет, эта цифра является правильной знаковой цифрой частного (то есть,
), полученная по знаку нулевого остатка в соответствии с алгоритмом деления без восстановления остатка, здесь указывает на переполнение разрядной сетки. Если же переполнения разрядной сетки нет, эта цифра является правильной знаковой цифрой частного (то есть, 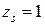 ).
).
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Знаки всех других остатков в этом случае определяют инверсные значения цифр частного.
В результате будет записан обратный код отрицательного частного.
Для округления и получения дополнительного кода результата необходимо добавить единицу в младший разряд, если полученный остаток не равен нулю: (Z=Z’+1).
Случай№4 X < 0; Y < 0.
На первом шаге алгоритма для формирования правильного знака частного (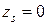 ), необходимо из отрицательного делимого вычитать отрицательный делитель (
), необходимо из отрицательного делимого вычитать отрицательный делитель (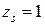 соответствует переполнению разрядной сетки). Далее же этот случай сводится к третьему.
соответствует переполнению разрядной сетки). Далее же этот случай сводится к третьему.
Здесь все цифры частного, включая псевдознаковую, равны знакам остатков.
В случае, когда полученный остаток равен нулю, к частному следует прибавить единицу (Z=Z’+1).
При использовании методов с восстановлением остатка и без восстановления остатка сдвиг влево может вызвать передачу значащей цифры из старшего разряда остатка в знаковый, и остаток будет искажен.
Поэтому надо оперировать двумя знаковыми разрядами.
Правильный знак при этом находится в дополнительном знаковом разряде, а единица в основном относится к разряду переполнения (в случае правильных дробей - к разряду целых).
Знак остатка от деления должен совпадать со знаком делимого.
Например: необходимо разделить два беззнаковых числа (21: 7=3).
Для удобства возьмем длину разрядной сетки равную четырем битам, а именно:
Х = 21 – делимое;
Y = 7 – делитель;
Z = 3 – частное.
Если (Z) и (Y) равняется четырем битам, то как было отмечено выше (X) должно быть восьмиразрядным значением, т.е длина разрядной сетки делимого в два раза больше делителя и частного.
Алгоритм деления приведен в табл. 4.10.
Таблица 4.10 - Алгоритм деление целых двоичных знаковых чисел методом без восстановлением остатка.
| Регистр (В) делимое X | Регистр (С) делитель Y | Регистр (А) частное Z | Счетчик тактов (Сч.Т) | |||||||||||||||||
| < 0 | ||||||||||||||||||||
| < 0 | ||||||||||||||||||||
| < 0 | ||||||||||||||||||||
| > 0 | ||||||||||||||||||||
| > 0 | ||||||||||||||||||||
| СТОП | ||||||||||||||||||||
Для закрепления материала рекомендуется выполнить следующие упражнения:
1. Перевести в двоичную систему счисления и вычислить выражение:
((19(10) – 15(10)) * (18(10) – 11(10)))/7(10).
2. Перевести в двоичную систему счисления и вычислить выражение:
((10(10) – 15(10)) * (18(10) – 12(10)))/6(10).
3. Перевести в двоичную систему счисления и вычислить выражение:
((17(10) – 12(10)) * (23(10) – 17(10)))/(-6(10)).
4. Перевести в двоичную систему счисления и вычислить выражение:
((25(10) – 21(10)) * (10(10) – 17(10)))/(-7(10)).
5. Перевести в двоичную систему счисления и вычислить выражение:
((14(10) – 21(10)) * (10(10) – 16(10)))/5(10).
6. Перевести в двоичную систему счисления и вычислить выражение:
((15(10) – 11(10)) * (12(10) – 17(10)))/5(10).
Лекция № 13 (90-минут)
Тема: Выполнение арифметических операций в компьютерных системах над числами с плавающей точкой
Каждой форме представления чисел (с фиксированной или плавающей точкой) свойственны свои преимущества и недостатки. Поэтому в современных компьютерных системах обычно имеется возможность использования любой из них. Компьютерные средства, в которых используется преимущественно представление чисел в форме с фиксированной точкой, представляют собой специализированные компьютерные системы для управления технологическими процессами, обработки статистической информации и результатов измерений, решения задач с большим числом логических операций и т.д. Представление же чисел в форме с плавающей точкой используется в компьютерных системах, которые служат для решения широкого круга задач научного и технического характера. Это обусловлено тем, что использование формы с плавающей точкой позволяет значительно расширить диапазон представимых чисел, по сравнению с фиксированной точкой, обеспечивая при этом высокую точность представления.
 . (5.1)
. (5.1)
где M — мантисса;
P — порядок.
При представлении чисел в форме с плавающей точкой мантисса может быть любым знаковым числом: целым, правильной дробью, смешанным числом. Однако условие нормализации предполагает представление мантиссы в виде правильной дроби:
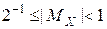 . (5.2)
. (5.2)
где M — мантисса.
Знак мантиссы определяет знак всего числа.
Порядок определяет фактическое положение запятой вместо положения, которое она занимает в изображении мантиссы, и может быть положительным или отрицательным, но обязательно целым числом. Понятие «ПЗ» можно рассматривать как перемещение запятой в изображении числа влево, если Р< 0, или вправо, если P> 0. Для обозначения чисел с плавающей точкой используют форму вида:
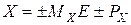 . (5.3)
. (5.3)
где М – мантисса числа;
Е – разделитель мантиссы и порядка;
Р – порядок числа.
Вместо E могут использоваться другие символы, например, D (double — двойная точность), когда для мантиссы отводится большее количество разрядов. Если для записи порядка используется (Р) разрядов, а для записи мантиссы (М) разрядов, то в форме с плавающей точкой может быть представлено следующее максимальное (по абсолютной величине) число:
 (5.4)
(5.4)
В свою очередь, минимальное по абсолютной величине, но не равное нулю, число в форме с плавающей точкой может быть представлено в виде:
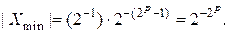 (5.5)
(5.5)
При получении последней оценки полагаем, что минимальное значение мантиссы равно (2-1) из-за условия нормализации. Подобные рассуждения применимы и для определения максимального и минимального отрицательных чисел, поскольку они представляются в компьютерных системах. В компьютерных системах, где используется представление чисел в форме с плавающей точкой, арифметические операции выполняются как над мантиссами операндов, так и над их порядками. При этом часто необходимо выполнять операцию нормализации чисел. Поэтому процессоры с плавающей точкой являются более сложными и менее быстродействующими, чем процессоры с фиксированной точкой (естественно, при сравнимом быстродействии электронных компонентов этих процессоров). Вместе с тем, в компьютерных системах с фиксированной точкой возникают определенные трудности из-за необходимости масштабирования данных. Кроме того, здесь значительно уже диапазон представимых чисел. В этом легко убедиться, сравнивания отношения для различных форм представления числовых данных:
 (5.6)
(5.6)
Для чисел с плавающей точкой:
 (5.7)
(5.7)
Из рассмотренного следует, что диапазон представления чисел в форме с плавающей точкой зависит от разрядности порядка. Увеличение разрядности порядка на (1) значительно расширяет диапазон (таблица 5.1).
Таблица 5.1- Зависимость диапазона представимых чисел от разрядности порядка
| P | 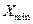
| 
|

| 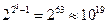
| |
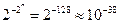
| 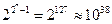
| |
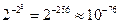
| 
|
Хотя диапазон представления чисел в форме с плавающей точкой во много раз шире диапазона представления чисел с фиксированной точкой, тем не менее в процессе вычислений могут возникать ситуации, когда результат вычислений выходит за пределы диапазона.
5.2 Форматы двоичных числовых данных с плавающей точкой
Формат данных с плавающей точкой, использовавшийся в компьютерных системах первых поколений, включал четыре поля, а именно: указанные ранее поля для мантиссы и ее знака (длиной (m+1) разряд), а также два дополнительных поля для порядка и его знака (длиной (p+1) разряд).
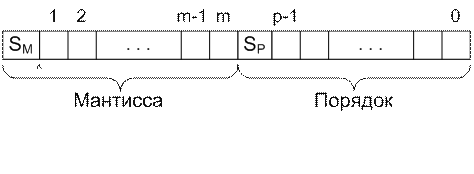
Рисунок 5.1 — Классический формат данных с плавающей точкой
В отличие от рассмотренного выше классического формата, в современных компьютерных системах используют смещенный порядок, т.е. порядок, представленный в смещенном коде.
Смещенный порядок (Ех) представляет собой целое беззнаковое число, равное истинному порядку, увеличенному на некоторое значение смещения.
Такой прием устраняет необходимость использования знака порядка, давая возможность манипулировать порядками как целыми беззнаковыми числами.
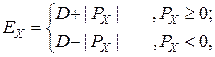 . (5.8)
. (5.8)
где 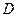 — некоторая константа (смещение).
— некоторая константа (смещение).
Если Рх > Рy, то Ex > Ey. Если (D = 2p-1), то такой смещенный код называют кодом с положительным нулем. Для перехода от смещенного кода к дополнительному достаточно проинвертировать знаковый бит.
Широко применяются смещенные коды с отрицательным нулем, когда
(D = 2p-1 - 1). При сложении и вычитании смещенных порядков результирующий порядок также должен быть смещенным.
При использовании смещенных кодов с отрицательным нулем сложение порядков выполняется в соответствии с правилом:
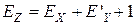 , (5.9)
, (5.9)
где Е’y - смещенный порядок с инвертированным старшим разрядом.
В этом случае может возникать как положительное, так и отрицательное переполнение. Если во втором слагаемом старший разряд (1) был инвертирован в (0), а при сложении возник перенос (CY=1), то имеет место переполнение порядка. Результат оказывается за пределами представления. Признаком получения отрицательного переполнения (антипереполнение) является отсутствие переноса (CY=0) из старшего разряда суммы при условии, что во втором слагаемом старший разряд из (0) был инвертирован в (1).
При вычитании смещенных порядков для получения смещенного порядка разности необходимо выполнить следующее действие:
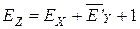 , (5.10)
, (5.10)
где Е’y - инверсное значение смещенного порядка с инвертированным старшим разрядом.
5.3 Стандарт IEEE-754
К настоящему времени разработаны многочисленные варианты форматов чисел с плавающей точкой и практической реализации арифметических устройств с плавающей точкой. Это, в свою очередь, создает трудности при написании переносимых программ, согласовании правил обработки числовых данных и т.д.
Поэтому был разработан международный стандарт IEEE-754, нормам которого должны удовлетворять практически все вновь разрабатываемые компьютерные системы. Указанный стандарт решает следующие задачи:
- упорядочивает форматы чисел с плавающей точкой;
- унифицирует реакции на особые случаи в процессе обработки;
- определяет требования к точности вычислений.
В соответствии со стандартом IEEE-754 определены два базовых и два расширенных формата. Во всех форматах используется смещенный код порядка. Мантисса имеет старший разряд (m0) с весом (20), относящийся к целой части. Поэтому условие нормализации изменяется:
 . (5.11)
. (5.11)
Базовый одинарный формат - (БОФ) имеет длину в 32 разряда. Поле порядка в этом формате содержит 8 разрядов, а смещение равно 127.
Максимальный положительный порядок числа здесь равен +127, минимальный отрицательный -128.
Базовый двойной формат - (БДФ) имеет одноразрядное знаковое поле, 11-разрядное поле смещенного порядка и 52-разрядное поле мантиссы.
Смещение здесь равно 1023. Особенность двух указанных форматов заключается в том, что минимальный и максимальный смещенные порядки зарезервированы для представления специальных чисел. Поля мантисс в явном виде не содержат разряда (m0), так как в памяти должны храниться нормализованные мантиссы чисел, а значит, их старший разряд всегда равен (1). При передаче числа из памяти в процессор этот «неявный» разряд становится «явным», и в операциях участвует 24-разрядная (БОФ) или 56-разрядная (БДФ) мантисса.
Расширенный одинарный формат - (РОФ) не имеет жестко фиксированных параметров, однако для конкретных реализаций он устанавливается, исходя из следующих требований:
- наличие одноразрядного знакового поля;
- наличие явного или скрытого разряда в мантиссе;
- длина мантиссы не менее 31 разряда;
- диапазон значений порядка — -1023... +1024.
Расширенный двойной формат - (РДФ) отличается от одинарного тем, что диапазон порядка составляет -16383...+16384, а поле мантиссы - не менее 63 разрядов. В качестве примера практической реализации форматов стандарта IEEE-754 можно рассмотреть представление числовых данных с плавающей точкой в компьютерных системах. Здесь используются данные трех типов (таблица 5.2):
- вещественные числа одинарной точности (single real), соответствующие БОФ;
- вещественные числа двойной точности (double real), соответствующие БДФ;
- вещественные числа расширенной точности (extended real) или временные вещественные числа, соответствующие РДФ.
Временные вещественные числа имеют в своем представлении явный бит (m0). В памяти компьютера числа хранятся чаще всего в форматах БОФ или БДФ, а их обработка выполняется в РДФ.
Следует отметить, что целые числа в диапазоне (2-64….2+64 ) представляются абсолютно точно в РДФ.
Таблица 5.2 - Зависимость диапазона представимых чисел от базовых форматов
| Тип | Длина | Точность | Диапазон (дв.) | Диапазон (дес.) |
| БОФ | 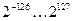
| 
| ||
| БДФ | 
| 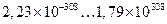
| ||
| РДФ | 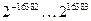
| 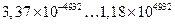
|
Если в процессе вычислений результат выходит за пределы представимых чисел, то имеет место особый случай:
- нарушение нормализации;
- если результат превышает |Xmax|, то такой случай называют переполнением или переполнением порядка, и вычисления при этом останавливают (прерывание);
- если результат меньше |Xmin|, имеет место антипереполнение или исчезновение порядка, что обычно воспринимается как нулевой результат (машинный 0);
- в результате выполнения сложения-вычитания мантисса может оказаться равной (0) при ненулевом порядке. Это ситуация потери значимости (псевдонуль). Результат интерпретируется как машинный (0).
Лекция № 14 (90-минут)
Тема: Принципы выполнения арифметических операций над числами в форме с плавающей точкой
Пусть требуется выполнить некоторую арифметическую операцию над операндами X и Y в форме с плавающей точкой:
 . (5.12)
. (5.12)
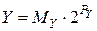 . (5.13)
. (5.13)
Результатом операции будет число:
 . (5.14)
. (5.14)
Порядки чисел X и Y представлены p разрядами, а мантиссы – (m-разрядные) правильные дроби, то есть,
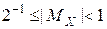 ,
, 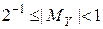 . (5.15)
. (5.15)
5.5 Сложение и вычитание чисел в форме с плавающей точкой
Представим операцию сложения в виде:
Z = X + Y. (5.16)
Пусть Рх > Py, тогда:
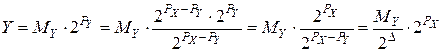 . (5.17)
. (5.17)
где 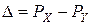 .
.
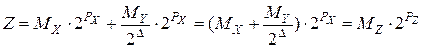 . (5.18)
. (5.18)
где 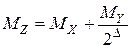 ;
; 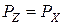 .
.
Операция сложения и вычитания операндов в форме с плавающей точкой включает следующие этапы:
- выравнивание порядков операндов и определение порядка результата;
- сложение и вычитание мантисс;
- нормализация результата;
- округление результата.
Выравнивание порядков необходимо для того, чтобы цифры мантисс с определенными весами располагались в соответствующих им разрядах регистров. Выполняется такая операция путем сдвига вправо мантиссы того операнда, порядок которого меньше. (Не выравнивать в сторону меньшего порядка! — теряем значащие цифры). Алгоритм выравнивания порядков сводится к следующему:
- сформировать разность порядков 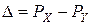 .
.
- если D> 0, то сдвинуть на один разряд вправо мантиссу (Y) и вычесть единицу из разности порядков(D); если D< 0, то сдвинуть на один разряд вправо мантиссу (X) и прибавить единицу к разности порядков (D);
- пункт 2 алгоритма повторять до тех пор, пока выполняется неравенство D≠ 0; при D=0 выравнивание порядков считают законченным.
Так как порядки операндов могут иметь разные знаки, то для представления их разности (D) может понадобиться (p+1) разряд. Абсолютная величина (D) может превышать число разрядов (m), отводимых для представления мантисс. В этом случае все разряды сдвигаемой вправо мантиссы выходят за пределы разрядной сетки и далее, при сложении и вычитании мантисс, абсолютная величина мантиссы, которая оставалась неподвижной, не меняется. Следовательно, при выполнении условия |D|> m можно прекратить выравнивание порядков и присвоить окончательному результату значение операнда, мантисса которого не сдвигалась.
Определять порядок результата удобно вместе с выравниванием порядков операндов. Порядок результата равен порядку большего по абсолютной величине операнда (то есть, того, мантисса которого не сдвигалась при выравнивании порядков).
Сложение и вычитание мантисс, для представления которых обычно используется прямой код, выполняется по тем же алгоритмам, что и чисел в форме с фиксированной точкой. Однако переполнение разрядной сетки здесь не приводит к остановке вычислений, что, как правило, имеет место при выполнении операций над числами в форме с фиксированной точкой. Наличие переполнения учитывается далее при нормализации результата.
Поскольку при выравнивании порядков возможна потеря части разрядов мантиссы одного из операндов, то мантисса результата может быть получена с погрешностью, по абсолютной величине почти равной единице младшего разряда. Однако среднее значение погрешности при этом равно нулю, если считать, что знаки " +" и " -" операндов и заданных операций появляются с равными вероятностями. С целью уменьшения максимальной абсолютной величины этой погрешности может быть введена операция округления мантиссы результата.
Необходимость нормализации результата обусловлена тем, что при мантиссах операндов, удовлетворяющих условиям нормализации, в зависимости от знака операции, мантисса результата может находиться в пределах 0≤ |z|< 2.
Таким образом, при сложении и вычитании мантисс может произойти нарушение нормализации мантиссы результата на один разряд влево или на произвольное число разрядов вправо. Нормализация результата выполняется следующим образом:
- если 1≤ |z|< 2 (нормализация нарушена влево), то сдвинуть мантиссу результата на один разряд вправо и прибавить единицу к порядку результата.
При этом может возникнуть переполнение порядков.
- при сложении мантисс близких по модулю друг к другу, но имеющих разные знаки может возникнуть нарушение нормализации вправо на любое число разрядов (вплоть до получения нулевой мантиссы).
Если 0< |z|< 1/2, то сдвинуть мантиссу влево и вычесть единицу из порядка результата. Эти действия продолжать до тех пор, пока сохраняются условия указанного выше неравенства (если мантисса результата представлена прямым кодом, то до тех пор, пока в старшем разряде мантиссы в результате сдвига появится единица). В этом случае может возникнуть антипереполнение.
Если |z|=0, то результату присваивается машинный нуль (потеря значимости), а выполнять нормализацию нет необходимости.
При использовании модифицированного дополнительного кода для вычитания левое нарушение нормализации обнаруживается так же, как и в предыдущем случае, а правое нарушение — по комбинациям 00, 0... и 11, 11....
5.6 Умножение и деление чисел в форме с плавающей точкой
Представим операцию умножения в виде:
Z = X · Y. (5.19)
тогда:
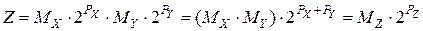 . (5.20)
. (5.20)
где:  ;
; 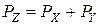 .
.
Знак произведения определяют путем суммирования по модулю 2 цифр в знаковых разрядах сомножителей: 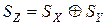 .
.
При умножении чисел в форме с плавающей запятой порядок результата определяется путем сложения порядков сомножителей. Для определения мантиссы результата производят умножение мантисс операндов как чисел с фиксированной точкой по любому из рассмотренных алгоритмов. Мантисса произведения может оказаться ненормализованной, причем возможно только правое нарушение нормализации на один разряд. В этом случае мантиссу надо удвоить, сдвинув ее на один разряд влево, а из порядка произведения вычесть единицу.
Представим операцию деления в виде:
Z = X/Y. (5.21)
Следует помнить, что при делении чисел с плавающей точкой остатка не бывает:
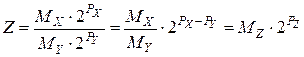 (5.22)
(5.22)
где: 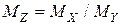 ;
; 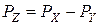 .
.
Знак частного обычно определяют путем суммирования по (модулю 2) цифр в знаковых разрядах делимого и делителя. При делении чисел в форме с плавающей точкой порядок частного находят как разность порядков операндов (из порядка делимого вычитается порядок делителя). Мантиссу частного получают в результате деления абсолютных величин мантисс операндов. При делении нормализованных мантисс, как правильных дробей, может иметь место нарушение нормализации влево на один разряд.
Таким образом, при умножении и делении чисел в форме с плавающей точкой над порядками выполняются только операции сложения и вычитания.
Для этого удобно использовать дополнительные коды. В процессе выполнения операций над порядками возможно как переполнение порядков, так и антипереполнение.
Общий алгоритм выполнения операций умножения и деления:
- определение знака результата;
- сложение и вычитание порядков;
- умножение и деление мантисс;
- нормализация результата;
- округление результата.
Как отмечалось ранее, необходимость округления результата вызвана тем, что при нормализации результата может выполняться правый сдвиг мантиссы результата и младший ее разряд при этом выходит за пределы разрядной сетки. Если считать, что результат представлен прямым кодом, то отбрасывание этого разряда вносит в абсолютную величину результата либо нулевую погрешность (если отбрасывается цифра 0), либо погрешность, равную 1/2 веса младшего разряда (если отбрасывается цифра 1). Для того, чтобы погрешность по абсолютной величине результата была знакопеременной и ее среднее значение в достаточно большой последовательности операций было равно нулю, округление следует производить следующим образом. Если за пределы разрядной сетки сдвигается цифра (1), то младший разряд мантиссы результата устанавливают в единицу независимо от того, какая цифра была в этом разряде ранее. В другом случае значение младшего разряда не меняют.
Пусть(хm) - младшая цифра мантиссы результата до округления, (х'm) - та же цифра после округления, (xm+1) - цифра мантиссы, выходящая за пределы разрядной сетки при округлении, (d) - погрешность округления. Тогда все возможные ситуации при округлении иллюстрируются табл. 11.4, из которой видно, что при таком округлении погрешность абсолютной величины мантиссы результата будет равна 0 или ±1/2 веса младшего разряда, а ее среднее значение равно нулю.
Таблица 5.3 – Результаты округления мантиссы результата
| xm | xm+1 | x’m | d |
| +(1/2)2-m | |||
| -(1/2)2-m |
5.7 Алгоритмы выполнения операций над числами в форме с плавающей точкой, в представлении IEEE-754
Вещественное число может быть представлено в каком-либо формате стандарта IEEE-754 следующим образом:
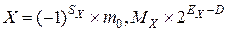 . (5.23)
. (5.23)
С учетом условия нормализации (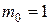 ), минимальные и максимальные абсолютные значения мантисс:
), минимальные и максимальные абсолютные значения мантисс:
 . (5.24)
. (5.24)
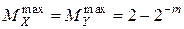 . (5.25)
. (5.25)
Сложение, вычитание, умножение и деление вещественных чисел в формате IEEE-754 осуществляется в соответствии с рассмотренными ранее алгоритмами. Поскольку в форматах хранятся не истинные значения порядков, а смещенные коды порядков, имеют место некоторые особенности, связанные с выполнением операций над смещенными порядками. Кроме того, должен учитываться факт наличия бита (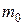 ) мантиссы.
) мантиссы.
При сложение и вычитании сравнение смещенных порядков осуществляется путем вычитания смещенных кодов как целых беззнаковых чисел. Сложение мантисс выполняется по правилам сложения целых знаковых чисел. Если получен отрицательный результат, то он представлен в дополнительном коде и его необходимо преобразовать в прямой код.
При умножении смещенный порядок произведения определяется в соответствии с рассмотренными выше правилами. Мантисса произведения может иметь нарушение нормализации.
Проанализируем различные ситуации:
1. 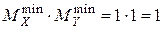 .
.
Нет нарушения нормализации.
2. 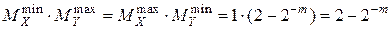
Нет нарушения нормализации.
3. 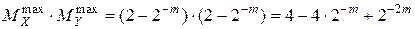 .
.
Здесь имеет место нарушение нормализации влево на 1 разряд.
При делении смещенный порядок частного определяется в соответствии с рассмотренными выше правилами. Мантисса частного может иметь нарушение нормализации. Проанализируем различные ситуации:
1. 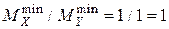 .
.
Нет нарушения нормализации.
2. 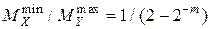 ; 0, 5< Z< 1
; 0, 5< Z< 1
Нарушение нормализации вправо на 1 разряд.
3. 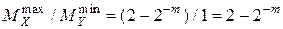 ; 1< Z< 2
; 1< Z< 2
Нет нарушения нормализации.
4. 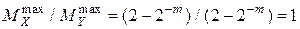 .
.
Нет нарушения нормализации.
Лекция № 15 (90-минут)
Тема: Представление числовых данных в коде BCD
Наиболее широкое применение в компьютерной технике получили двоично-десятичные системы счисления, в которых десятичные цифры записываются как четырехразрядные двоичные числа – двоичные тетрады.
Такое представление десятичных цифр называют также безизбыточным, поскольку для него необходимо минимальное количество двоичных разрядов.
Ограниченное применение находят и избыточные представления десятичных цифр с помощью пяти, шести и семи двоичных разрядов. В принципе, можно построить компьютерную систему, работающую при любом двоично-десятичном кодировании. Наличие разрешенных и запрещенных комбинаций является важным свойством BCD - кодов. В этом их отличие от обычных позиционных систем счисления.
Однако эмпирическим путем установлено, что для создания десятичных вычислительных средств наиболее целесообразно использовать двоично-десятичные коды (BCD или ДДК), обладающие свойствами взвешенности, упорядоченности, четности, дополнительности и единственности (так называемыми свойствами Рутисхаузера).
ДДК называется взвешенным, если каждому из (h) разрядов двоичного представления (ahah-1...a1) десятичной цифры (А) поставлены в соответствие веса – (gh, gh-1, …, g1) причем:
A=ahgh+ah-1gh-1+...+a1g1. (6.1)
где: А - десятичная цифра;
(ahah-1...a1) -) разряды двоичного представления;
(gh, gh-1, …, g1) – веса.
Свойство взвешенности упрощает выполнение логических и арифметических операций. ДДК, получаемые друг из друга простой перестановкой весов (gi), образуют кодовую группу. Для обозначения конкретных ДДК и кодовых групп часто используют последовательность их весов, записанную в порядке их убывания, например, " 8, 4, 2, 1", " 4, 4, 2, 1" и т.п.
Упорядоченность ДДК состоит в выполнении одного из условий:
0(2)< 1(2)< 2(2)<...< 9(2). (6.2)
0(2)> 1(2)> 2(2)>...> 9(2). (6.3)
для двоичных представлений (0(2), 1(2), 2(2),..., 9(2)) десятичных цифр. Наличие упорядоченности ДДК необходимо для реализации логических операций.
Свойство четности должно проявляться в том, чтобы всем четным десятичным цифрам соответствовали либо только четные, либо только нечетные их двоичные представления. Аналогично, всем нечетным десятичным цифрам должны соответствовать либо только нечетные, либо только четные их двоичные представления. Это свойство необходимо для реализации операций умножения, деления, округления. Сущность свойства дополнительности («самодополняемость») ДДК заключается в следующем. Если сумма двух десятичных цифр равна (9), то переход от двоичного представления одной цифры к двоичному представлению другой цифры должен осуществляться путем инверсии двоичных разрядов.
Наличие этого свойства необходимо для упрощения алгебраических операций (операций с учетом знаков операндов) по правилам десятичной арифметики. ДДК обладает свойством единственности, если между десятичной цифрой и комбинацией двоичных цифр установлено взаимно однозначное соответствие. Это свойство упрощает и облегчает как процедуру представления в ДДК десятичных чисел (то есть, кодирование), так и процедуру распознавания десятичных чисел в ДДК (то есть, декодирование).
Особенностью взвешенных ДДК, имеющих только положительные веса, кроме ДДК группы " 8, 4, 2, 1", является отсутствие однозначного представления десятичных цифр. Это означает, что некоторые десятичные цифры могут быть записаны несколькими комбинациями двоичных цифр. Например, в ДДК " 4, 4, 2, 1" цифру 4 можно представить как 1000 и как 0100, цифру 5 – как 1001 и как 0101, цифру 6 – как 1010 и как 0110, цифру 7 – как 1011 и как 0111. Причиной этого служит неоднозначность решения уравнения (6.1) относительно переменных ai (i=l, h).
Однозначность представления десятичных цифр, состоящая в том, что каждой такой цифре соответствует только одна из 16 двоичных тетрад, обеспечивается в ДДК группы " 8, 4, 2, 1".
Кроме того, однозначность представления десятичных цифр может быть обеспечена в ДДК с отрицательными весами. В табл. 6.1 приведены все кодовые группы однозначных ДДК. Следует отметить, что однозначность не входит в перечень свойств тех ДДК, которые наиболее целесообразно использовать для построения десятичных компьютерных систем.
Таблица 6.1 – Кодовые группы однозначных ДДК
| «8, 4, 2, 1» | «8, -4, 2, 1» | «8, -6, 4, 1» | «8, -4, 3, 2» | «8, -5, 4, 2» |
| «8, 4, 2, -1» | «8, 4, 3, -2» | «8, -6, 5, 3» | «7, -6, 5, 3» | «8, -4, -2, 1» |
| «8, 4, -2, 1» | «8, 6, -4, 1» | «8, 4, -3, 2» | «8, -4, 2, -1» | «8, 5, -4, 2» |
| «8, -4, 3, -2» | «7, 6, -5, 3» | «8, 4, -3, -2» | «8, 5, -4, -2» | «8, 6, -4, -1» |
| «8, 7, -4, -2» |
В этом перечне ему соответствует более слабое свойство единственности. Это свойство для неоднозначных ДДК может быть обеспечено выбором одной и исключением из ДДК избыточных (хотя, в принципе, правильных) двоичных представлений десятичных цифр. В этом отношении свойство единственности ДДК не эквивалентно свойству однозначности систем счисления, так как единственность ДДК можно обеспечить искусственно, а однозначность должна быть присуща счислению «органически». Существует 86 кодовых групп безизбыточных ДДК, обладающих свойствами взвешенности и единственности. Среди них есть ДДК, отрицательными весами, например, " 8, 4, 2, 1", " 8, 4, 2, -1", " 6, 3, -1, -1". Свойством дополнительности обладают все взвешенные ДДК с положительными весами, у которых сумма весов равна (9). Существуют четыре кодовых группы взвешенных ДДК, обладающих также и свойствами единственности и дополнительности, с именно: " 5, 2, 1, 1", " 4, 3, 1, 1", " 4, 2, 2, 1", " 3, 3, 2, 1". Среди взвешенных ДДК с отрицательными весами свойствами единственности и дополнительности обладают ДДК из 19 кодовых групп, перечисленных в табл. 6.2.
Таблица 6.2 – Кодовые группы ДДК с отрицательными весами, обладающие свойствами единственности, дополнительности и взвешенности
| «6, 3, 1, -1» | «7, 3, 1, -2» | «6, 4, 1, -2» | «6, 5, 1, -3» | «7, 5, 1, -4» |
| «6, 2, 2, -1» | «5, 3, 2, -1» | «6, 3, 2, -2» | «8, 3, 2, -4» | «4, 4, 2, -1» |
| «6, 4, 2, -3» | «8, 4, 2, -5» | «6, 5, 2, -4» | «4, 4, 3, -2» | «5, 4, 3, -3» |
| «8, 4, 3, -6» | «7, 5, 3, -6» | «8, 4, -2, -1» | «8, 6, -1, -4» |
Упорядоченность присуща лишь ДДК, не имеющим отрицательных весов. Одновременно свойствами единственности, упорядоченности, дополнительности и взвешенности обладают ДДК кодовых групп " 5, 2, 1, 1", " 4, 3, 1, 1", " 3, 3, 2, 1", " 4, 2, 2, 1". Всеми пятью свойствами обладают ДДК кодовой группы " 4, 2, 2, 1", называемые также кодами Эмери (" 2, 4, 2, 1" – код Айкена).
Недостатком ДДК этой кодовой группы является искусственный порядок весов, что затрудняет выполнение арифметических операций.
Наиболее распространенным в компьютерных системах является ДДК " 8, 4, 2, 1", который называется также кодом прямого замещения. Этот ДДК получают путем записи десятичных цифр в двоичной позиционной однородной системе счисления с естественным порядком весов. Он обладает всеми перечисленными выше свойствами ДДК, кроме свойства дополнительности. Этим обусловлен ряд неудобств при реализации операций алгебраического сложения в таком ДДК из-за трудностей формирования переносов из младшей тетрады в старшую. Достоинством ДДК " 8, 4, 2, 1" следует считать простоту и удобство перевода чисел из десятичной системы счисления в двоично-десятичную и обратный перевод. В каждом конкретном случае применение какого-либо ДДК обуславливается определенными его преимуществами по сравнению с другими типами ДДК. Например, код " 7, 4, 2, 1" применяется в электромеханических цифровых устройствах, где двоичной единице соответствует замкнутое состояние некоторой контактной пары и энергопотребляющее состояние соответствующей электрической цепи, а двоичному нулю - разомкнутое состояние контактной пары и не потребляющее энергии состояние электрической цепи. В этом случае каждое двоичное представление десятичной цифры содержит не более двух единиц, что обеспечивает минимальное и постоянное потребление энергии от источника питания. В ДДК " 5, 4, 2, 1", десятичные цифры можно рассматривать как двоично-пятеричные с кодированным представлением цифр. Три младших разряда в каждой тетраде изображают одну пятеричную цифру, с старшая цифра тетрады соответствует двоичному разряду. Этот ДДК имеет ряд достоинств при выполнении арифметических операций и переводе чисел из одной системы счисления в другую.
Для представления десятичных цифр могут быть использованы и невзвешенные ДДК. Например, код " с избытком 3" обладает свойством дополнительности и его удобно использовать для выполнения операции алгебраического сложения. Для записи десятичной цифры в ДДК " с избытком 3" необходимо двоичную тетраду этой цифры в ДДК " 8, 4, 2, 1" сложить с двоичным представлением числа (3).
ДДК " 8, 4, 2, 1" и коды с избытком (полученные из кода " 8, 4, 2, 1" по аналогии с кодом " с избытком 3") обладают еще одним важным свойством, не входящим в перечень Рутисхаузера, а именно: свойством аддитивности. Это свойство состоит в том, что ДДК суммы двух десятичных цифр равен двоичной сумме ДДК этих цифр или отличается от нее на некоторую константу. Это свойство позволяет свести операции десятичной арифметики в таких ДДК к выполнению операций по правилам двоичной арифметики.
Примерами избыточных ДДК, где каждая десятичная цифра кодируется пятью двоичными разрядами, являются ДДК " 3А+2" и " 2 из 5". Первый из этих ДДК обладает свойством дополнительности, а двоичные представления десятичных цифр получают в нем путем записи в двоичной системе с естественным порядком весов числа ЗА+2, где А – заданная десятичная цифра.
В ДДК " 2 из 5" каждая десятичная цифра изображается пятью двоичными разрядами, из которых только два содержат единицы. Можно считать, что ДДК " 2 из 5" получается из ДДК " 7, 4, 2, 1" путем добавления справа дополнительного разряда с весом, равным нулю. В этот разряд записывают такую цифру, чтобы общее число единиц было равно двум (за исключением десятичного нуля). ДДК " 3А+2" и " 2 из 5" используют обычно для передачи информации, поскольку они позволяют обнаруживать одиночные ошибки, возникающие в процессе такой передачи, сравнительно простыми средствами.
Рефлексный ДДК (код Грея, соседний код) обладает тем свойством, что двум соседним десятичным цифрам в нем соответствуют кодовые комбинации, отличающиеся только в одном двоичном разряде. Это свойство эффективно используется при построении измерительных преобразователей (датчиков) величины углового или линейного перемещения в цифровой эквивалент.
ДДК – (w, x, y, z,) - обладает следующим свойством. Для десятичной цифры (А) в таком ДДК перестановка ее двоичных разрядов вида (z, w, x, y) равна младшему десятичному разряду (в двоичном представлении) произведения (А) на (3); перестановка вида (x, y, z, w) равна младшему разряду произведения (А) на (7); перестановка (y, z, w, x) равна младшему разряду произведения (А) на(9).
Таким образом, младший разряд произведения любой заданной десятичной цифры на (3, 7, 9) может быть получен круговой перестановкой двоичных цифр. Очевидно, что это свойство может использоваться для частичного контроля правильности выполнения десятичного умножения.
6.1 Форматы числовых данных BCD - кодов
В современных компьютерных системах, обрабатывающих не только числовую информацию, но и текстовую (алфавитно-цифровую), отдельные символы чаще всего представляются словами длиной в один байт. Так как байт равен двум двоичным тетрадам, то в компьютерных системах с байтовым представлением информации можно записывать две десятичные цифры в один байт. Такую запись называют также упакованной записью или упакованным форматом записи десятичных цифр. Вместе с тем, можно записывать в один байт и по одной десятичной цифре, используя остальные четыре разряда для записи знаков и вспомогательных символов. Такую запись называют распакованной записью или распакованным форматом. В компьютерных системах широкого назначения обычно реализуются обе возможности записи десятичных цифр. Рассмотрим упакованный десятичный формат. Младшая цифра занимает в байте правую тетраду (биты 3-0), а старшая – левую (биты 7-4). Обе цифры представлены в коде «8, 4, 2, 1». Многоразрядные упакованные десятичные числа занимают несколько байт. Для представления знака числа используют запрещенные кодовые комбинации: для «+» – C(16), для «–» – D(16). Код знака числа записывают в старшей тетраде старшего байта.
Распакованный формат называют символьным или ASCII - форматом.
Каждый байт содержит код, соответствующий десятичной цифре в кодовой таблице ASCII. В ней цифры имеют коды 30(16)-39(16). Таким образом, значение десятичной цифры представлено в младшей тетраде, а старшая тетрада является кодом «зоны» (3). Поэтому такой формат также называют зонированным. Для обозначения знака используют коды символов «+» и «–» из кодовой таблицы ASCII (2B(16) 2D(16) соответственно).
Лекция № 16 (90-минут)
Тема: Арифметические операции над числовыми данными BCD - кодов
Сложение и вычитание десятичных двоично-кодированных операндов может быть реализовано на основе тех же принципов, что и двоичных операндов с учетом лишь особенностей суммирования десятичных цифр в двоичном их представлении:
- правила формирования десятичного переноса отличаются от правил формирования двоичного переноса;
- сумма двоичных кодов десятичных цифр, полученная по правилам двоичной арифметики, не всегда равна их сумме, полученной по десятичным правилам.
По этим причинам при использовании ДДК, обладающих свойством аддитивности, суммирование десятичных цифр в двоичном представлении проводят в два этапа:
1) суммируют двоичные представления десятичных цифр по правилам двоичной арифметики;
2) проводят коррекцию предыдущего результата путем прибавления или вычитания некоторой поправки для образования правильного представления десятичной цифры и десятичного переноса в старший десятичный разряд.
Если же ДДК не обладает свойством аддитивности, то сначала выполняют преобразование цифр слагаемых в ДДК, обладающий таким свойством, далее суммируют цифры в аддитивном ДДК, а затем результат суммирования подвергают обратному преобразованию.
Рассмотрим, как можно определить корректирующую поправку и правильно сформировать перенос в старший десятичный разряд для ДДК " 8, 4, 2, 1". Для этого составим таблицу двоичных сумм, их представлений после первого этапа сложения, правильных их представлений в ДДК " 8, 4, 2, 1" десятичных переносов и корректирующих поправок (табл. 6.3).
Таблица 6.3 - Таблица двоичных сумм после первого этапа сложения
| Десятичная сумма | Сумма после первого этапа s5s4s3s2s1 | Правильная сумма pz4z3z2z1 | Коррекция с5с4с3с2с1 |
| 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 1 0 1 0 1 0 0 1 0 1 1 0 1 1 0 0 0 1 1 0 1 0 1 1 1 0 0 1 1 1 1 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 1 0 0 1 1 | 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 0 0 0 0 1 0 0 1 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 1 0 0 1 1 1 0 1 0 0 1 0 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 0 0 0 1 1 0 0 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 |
Из таблицы видно, что если результат, полученный на первом этапе, находится в пределах от 0 до 9, то корректировать его нет необходимости, а двоичный и десятичный перенос в этом случае совпадают. Если же результат первого этапа находится в пределах от 10 до 19, то для образования правильной суммы (pz4z3z2z1) к предварительной сумме (s5s4s3s2s1) необходимо прибавить корректирующую поправку (00110). Признаком нахождения суммы первого этапа в диапазоне от 10 до 19 может служить наличие единичного значения переноса p. Таким образом, если при прибавлении коррекции перенос (р=0), то как правильную сумму необходимо взять результат первого этапа, если же (p=l), то как правильную сумму необходимо взять откорректированный результат.
При сложении или вычитании многоразрядных десятичных операндов описанные действия должны выполняться по каждому десятичному разряду (в ДДК " 8, 4, 2, 1" – по каждой тетраде двоичных разрядов).
Умножение чисел в десятичной системе счисления с двоично-кодированным представлением цифр может быть реализовано на тех же принципах, что и в двоичной системе, то есть, имеется четыре основных алгоритма десятичного умножения, каждый из которых имеет свои преимущества и недостатки, аналогичные, в целом, преимуществам и недостаткам соответствующих алгоритмов двоичного умножения. Особенности же десятичного умножения состоят в следующем:
- результат умножения двух двоичных цифр представляется только одной цифрой произведения с весом, равным произведению весов цифр сомножителей; в отличие же от этого, результат умножения двух десятичных цифр будет представлен двумя цифрами – цифрой собственно произведения и с весом, равным произведению весов цифр сомножителей, и цифрой переноса q в разряде с весом, на единицу большим произведения весов цифр сомножителей;
- суммирование частичных произведений должно осуществляться по правилам десятичной арифметики (то есть, используются для этого десятичные сумматоры);
- сдвиг в регистрах осуществляется одновременно на один десятичный разряд;
- на каждом шаге умножения осуществляется столько суммирований множимого с суммой частичных произведений, сколько единиц содержится в очередной цифре множителя.
Для учета особенности при умножении с младших разрядов или при умножении со старших разрядов десятичный разряд регистра множителя снабжают цепями вычитания единиц и в каждом такте суммирования цифру в этом разряде уменьшают на единицу. Такты суммирования производят до тех пор, пока в десятичном разряде, управляющем умножением, не будет получен нуль. Если для представления десятичных цифр используется ДДК " 8, 4, 2, 1", то указанный десятичный разряд выполняют в виде счетчика.
При умножении по этому алгоритму на один разряд множителя в среднем приходится 4, 5 тактов суммирования (предполагаем, что цифры 0, 1,..., 9 появляются во всех разрядах множителя с равными вероятностями).
Деление десятичных чисел в компьютерных системах, как и двоичных чисел, можно выполнять по двум основным алгоритмам: с восстановлением остатка и без восстановления остатка. Реализация первого алгоритма требует несколько больших временных затрат (примерно на 12...17%) по сравнению со вторым.
В соответствии с этим алгоритмом сдвиг выполняется на один десятичный разряд, все суммирования и вычитания, а также формирование обратного и дополнительного кодов (в случае использования их для вычитания) должны выполняться по правилам десятичной арифметики. На каждый шаг деления здесь приходится несколько суммирований-вычитаний.
Для ускорения операции десятичного деления необходимо, в первую очередь, уменьшать число суммирований и вычитаний, выполняемых для получения одной цифры частного.
|
|
