Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Тема: Умножение двоичных знаковых чисел в компьютерных системах

При выполнении операции умножения знаковых чисел исходные сомножители могут быть представлены в ПК, ОК или ДК:

. (4.34)

При данном способе умножения знаковые и числовые разряды обрабатываются отдельно. Для определения знака произведения осуществляют суммирование (по модулю 2) цифр, записанных в знаковых разрядах операндов. Модуль произведения получают, перемножая модули сомножителей в соответствии с одним из рассмотренных ранее алгоритмов:

. (4.35)

Определение знака произведения показано в табл. 4.5. Где (0) - обозначает (+), а (1) – обозначает (-).

Таблица 4.5 – Определение знака произведения

0 0=0

0 1=1

1 0=1

1 1=0

Однако в современных компьютерах операнды в памяти обычно хранятся в ДК, что продиктовано, в частности, удобством выполнения операции сложения (учитывая автоматическое формирование знака суммы). Для того, чтобы умножить два числа, представленных в ДК можно использовать следующий прием: перед выполнением операции умножения исходные числа преобразуют в ПК, затем их перемножают, а результат далее переводят в ДК.

Такой прием не является эффективным. Поэтому на практике чаще всего используют специальные алгоритмы умножения чисел в дополнительных кодах. Алгоритмы корректного умножения операндов в ДК можно разделить на две группы:

- алгоритмы первой группы это алгоритмы с обработкой знаковых разрядов отдельно от числовых;

- алгоритмы второй группы это алгоритмы с обработкой знаковых разрядов вместе с числовыми. Т.е., на сумматоре дополнительных кодов в процессе перемножения машинных изображений операндов получают одновременно знаковую и числовую части произведения.

Теорема: произведение дополнительных кодов сомножителей равно дополнительному коду результата только в случае положительных сомножителей. Если хотя бы один сомножитель отрицателен, то произведение чисел на сумматоре дополнительных кодов получается прибавлением поправки (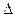) к произведению дополнительных кодов сомножителей. Рассмотрим арифметическое обоснование алгоритмов первой группы при различных вариантах комбинаций знаков операндов. С этой целью у операндов отбрасывается знаковая цифра и выполняется умножение полученных псевдомодулей по одному из известных алгоритмов. Результат такого умножения назовем псевдопроизведением (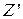). Обозначим вес знакового разряда сомножителей (). Тогда, в соответствии с рассмотренным ранее правилом формирования дополнительного кода, отрицательные сомножители будут представлены в ДК следующим образом:

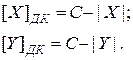. (4.36)

При удалении знакового разряда получаем псевдомодули:

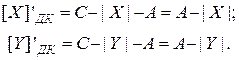. (4.37)

Всего возможны четыре варианта сочетания знаков сомножителей: