Квадратичных форм

Назовем r-м усечением квадратичной формы

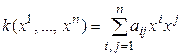(5.24)

квадратичную форму . Пусть

–

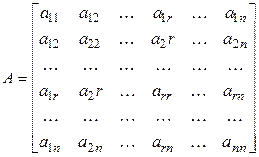матрица квадратичной формы (5.24). Главными минорами матрицы А называются ее миноры, расположенные в левом верхнем углу. Будем обозначать 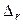главный минор r -го порядка матрицы А. Очевидно, что 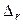совпадает с определителем матрицы квадратичной формы .

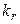Теорема 5.9 (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицы были положительными. Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицы нечетного порядка были отрицательными, а четного – положительными.

► Доказательство для положительной определенности.

Необходимость. Дано: квадратичная форма положительно определена. Тогда для любого нетривиального набора переменных 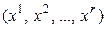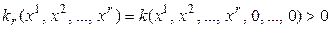, значит, положительно определена и квадратичная форма 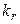, и поэтому 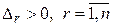, на основании следствия к теореме 5.8.

Достаточность. Дано: 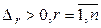. Доказательство проведем методом математической индукции по количеству переменных.

1. Проверяем утверждение при 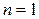. Имеем 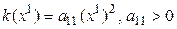, т. е. квадратичная форма k положительно определена.

2. Пусть утверждение верно для квадратичных форм от (n –1)-й переменной. Докажем его для квадратичных форм от n переменных.

Так как 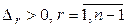, то, по предположению индукции, квадратичная форма 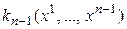положительно определена, а значит, существует линейное невырожденное преобразование переменных

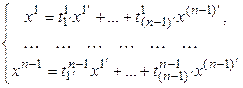(5.25)

с матрицей 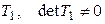, приводящее 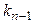к нормальному виду 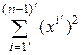. Рассмотрим следующее преобразование переменных:

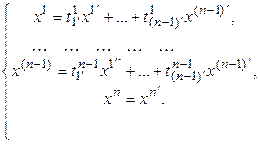. (5.26)

Если Т – матрица преобразования (5.26), то 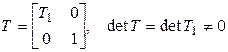, а значит, (5.26) – линейное невырожденное преобразование переменных. Применив (5.26) к форме (5.24), получаем:

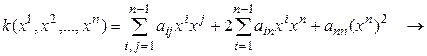[(5.26)]

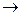
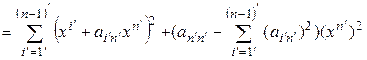. (5.27)

Обозначим 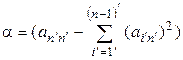и положим

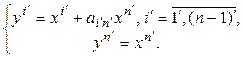(5.28)

Очевидно, (5.28) – линейное преобразование переменных с матрицей

.

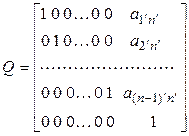Так как 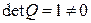, то (5.28) – линейное невырожденное преобразование переменных, которое переводит квадратичную форму (5.27) в квадратичную форму

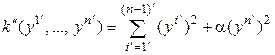. (5.29)

Применяя к форме (5.24) композицию преобразований (5.26) и (5.28), получаем квадратичную форму (5.29). Таким образом, (5.29) эквивалентна исходной квадратичной форме (5.24).

Обозначим 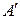матрицу формы (5.29). Так как при линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака и так как det A = 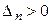, то

.

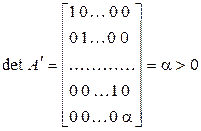Поэтому квадратичная форма (5.32) положительно определена согласно теореме 5.8, а значит, положительно определена и исходная квадратичная форма.

Доказательство для отрицательной определенности. Обозначим 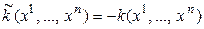, 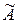– матрицу квадратичной формы 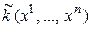, 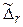– главные миноры матрицы 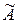. Тогда

{ k отрицательно определена} 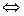{ 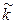положительно определена}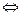

◄

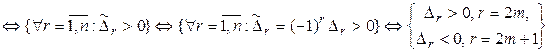Замечание. Можно доказать, что если хотя бы один минор четного порядка матрицы квадратичной формы есть число отрицательное, то эта квадратичная форма знаконеопределена.

Определение. Симметричная билинейная форма называется положительно определенной, если положительно определена соответствующая ей квадратичная форма.