Симметричные билинейные формы

Определение. Квадратная матрица 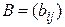называется симметричной, если 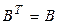, или если .

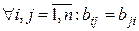Лемма 5.1. Если матрица симметрична, то любая конгруэнтная ей матрица тоже симметрична.

► Пусть – симметричная матрица, 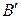– конгруэнтная ей. Тогда

.◄

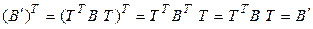Определение. Билинейная форма 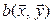на линейном пространстве V называется симметричной, если .

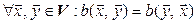Теорема 5.3. Для того чтобы билинейная форма 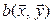на линейном пространстве была симметричной, необходимо и достаточно, чтобы ее матрица в некотором, а значит, и в любом базисе пространства была симметричной.

► Докажем утверждение для некоторого базиса, а для произвольного оно будет вытекать из доказанной леммы. Обозначим 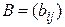матрицу билинейной формы 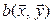в базисе .

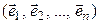Необходимость. Дано: 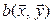– симметричная билинейная форма. Тогда 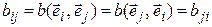и, таким образом, В – симметричная матрица.

Достаточность. Дано: В – симметричная матрица, т. е. 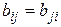. Тогда : = .◄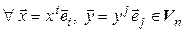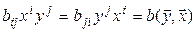