Квадратичные формы

Определение.Квадратичной формой, соответствующей симметричной билинейной форме 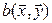на линейном пространстве V, называется функция одного векторного аргумента .

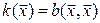Пусть задана квадратичная форма 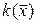, 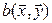– соответствующая ей симметричная билинейная форма. Тогда

,

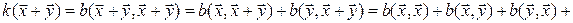
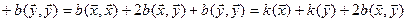
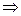
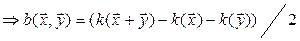откуда вытекает, что по квадратичной форме соответствующая ей симметричная билинейная форма тоже определяется однозначно. Итак, между симметричными билинейными и квадратичными формами на линейном пространстве V устанавливается взаимно однозначное соответствие, поэтому квадратичные формы можно изучать с помощью симметричных билинейных форм.

Рассмотрим n -мерное линейное пространство . Матрицей квадратичной формы в заданном базисе линейного пространства называется матрица соответствующей ей симметричной билинейной формы в том же базисе. Матрица квадратичной формы всегда симметрична.

Обозначим матрицу квадратичной формы в некотором базисе пространства . Если, как обычно, обозначить Х координатный столбец вектора 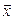в том же базисе, то из равенства 5.5 получаем матричную форма записи квадратичной формы:

.

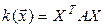Теорема 5.4. Пусть в линейном пространстве заданы два базиса

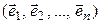(5.10)

и

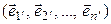, (5.11)

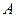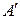и пусть и – матрицы квадратичной формы 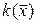в базисах (5.10) и (5.11) соответственно. Тогда 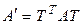, где Т – матрица перехода от (5.10) к (5.11).

Доказательство вытекает из теоремы 5.2 и определения матрицы квадратичной формы.

В связи с тем, что матрица перехода Т является невырожденной, то при переходе к новому базису ранг матрицы квадратичной формы не меняется. Поэтому можно сформулировать следующее определение.

Определение. Рангом квадратичной формы, заданной на линейном пространстве , называется ранг ее матрицы в некотором, а значит, и в любом базисе пространства (обозначается ).

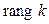Теперь запишем квадратичную форму в координатном виде. Для этого вектор 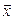разложим по базису (5.10): 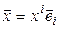. Если – матрица квадратичной формы 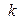в том же базисе, то в соответствии с равенством (5.4)имеем

– (5.12)

координатная форма записи квадратичной формы. Распишем (5.12) подробно при n = 3, учитывая, что

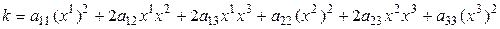. (5.13)

Итак, если в задан базис, то квадратичная форма в координатной записи выглядит как однородный многочлен второй степени от n переменных – координат вектора в данном базисе. Этот многочлен называется видом квадратичной формы 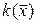в заданном базисе. Но в приложениях часто такие многочлены возникают самостоятельно, без видимой связи с линейными пространствами (например, вторые дифференциалы функций), поэтому мы сформулируем еще одно определение квадратичной формы.

Определение. Квадратичной формой от n переменных 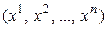называется однородный многочлен второй степени от этих переменных, т. е. функция вида (5.12). Матрицей квадратичной формы (5.12) называется симметричная матрица .

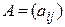Пример составления матрицы квадратичной формы. Пусть

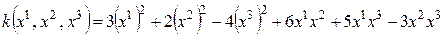. (5.14)

Из (5.12) и (5.13) видно, что коэффициент при 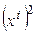совпадает с 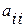, т.е. диагональные элементы матрицы квадратичной формы – это коэффициенты при квадратах. Точно так же видим, что 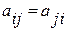– половина коэффициента при произведении 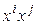. Таким образом, матрица квадратичной формы (5.14) выглядит так:

.

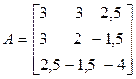Выберем теперь в пространстве опять два базиса (5.10) и (5.11) и обозначим, как обычно, 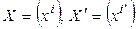– координатные столбцы вектора 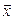в базисах (5.10) и (5.11) соответственно. При переходе от базиса (5.10) к базису (5.11) координаты вектора меняются по закону:

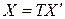, (5.15)

где 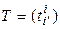- матрица перехода от (5.10) к (5.11). Заметим, что матрица 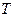– невырожденная. Запишем равенство (5.15) в координатной форме:

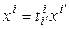, (5.16)

или подробно:

(5.17)

С помощью равенства (5.17) (или (5.16), что одно и то же) от переменных 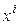переходим к переменным .

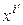Определение. Линейным невырожденным преобразованием переменных называется преобразование переменных, заданное системой равенств (5.16) или (5.17), или одним матричным равенством (5.15), при условии, что 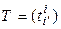– невырожденная матрица. Матрица Т называется матрицей этого преобразования переменных.

Если в (5.12) вместо переменных 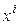подставить их выражения через переменные 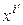по формулам (5.17), раскрыть скобки и привести подобные, то получим другой однородный многочлен второй степени:

.

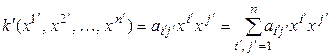В этом случае говорят, что линейное невырожденное преобразование переменных (5.17) переводит квадратичную форму 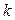в квадратичную форму 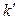. Значения переменных 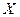и , связанные соотношением (5.15) (или соотношениями (5.16) либо (5.17)), будем называть соответствующими при заданном линейном невырожденном преобразовании переменных.

Определение. Набор переменных называется нетривиальным, если в нем значение хотя бы одной из переменных отлично от нуля. В противном случае набор переменных называется тривиальным.

Лемма 5.2. При линейном невырожденном преобразовании переменных тривиальному набору переменных соответствует тривиальный набор.

► Из равенства (5.15), очевидно, вытекает: если , то и . С другой стороны, используя невырожденность матрицы Т, опять же из (5.15) получаем 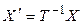, откуда видно, что при , также и .◄

Следствие. При линейном невырожденном преобразовании переменных нетривиальному набору переменных соответствует нетривиальный набор.

Теорема 5.5. Если линейное невырожденное преобразование (5.15) переводит квадратичную форму 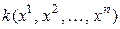с матрицей А в квадратичную форму 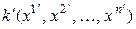с матрицей А', то 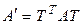(другая формулировка теоремы 5.4).

Следствие. При линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака.

Замечание. В отличие от матрицы перехода и матрицы линейного оператора, матрица линейного невырожденного преобразования переменных пишется не по столбцам, а по строкам.

Пусть заданы два линейных невырожденных преобразования переменных:

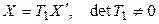, (5.18)

и

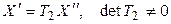. (5.19)

Применим их последовательно:

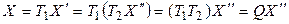. (5.20)

Композицией линейных невырожденных преобразований переменных (5.18) и (5.19) называется их последовательное применение, т. е. преобразование переменных Из (5.20) видно, что композиция двух линейных невырожденных преобразований переменных также является линейным невырожденным преобразованием переменных.

Определение. Квадратичные формы называются эквивалентными, если существует линейное невырожденное преобразование переменных, переводящее одну из них в другую.