
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение билинейной формы и ее различные формы записи
|
|
ГЛАВА 5. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
Билинейные формы
Определение билинейной формы и ее различные формы записи
Определение. Билинейной формой на линейном пространстве 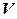 над полем
над полем 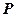 называется функция
называется функция 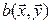 двух векторных аргументов, принимающая значения из поля
двух векторных аргументов, принимающая значения из поля 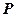 , линейная по каждому из своих аргументов, т. е. удовлетворяющая следующим условиям.
, линейная по каждому из своих аргументов, т. е. удовлетворяющая следующим условиям.
1*. 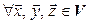 :
: 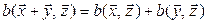 ;
;
2*. 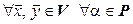 :
: 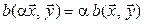 ;
;
3*. 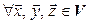 :
: 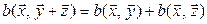 ;
;
4*. 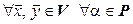 :
: 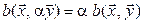 .
.
Рассмотрим n -мерное линейное пространство  и выберем в нем какой-либо базис:
и выберем в нем какой-либо базис:
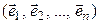 (5.1)
(5.1)
Каждый вектор пространства  можно разложить по этому базису:
можно разложить по этому базису: 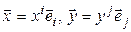 . Тогда
. Тогда
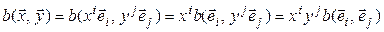 . (5.2)
. (5.2)
Из (5.2) видно, что значение билинейной формыдля любых двух векторов 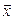 и
и 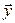 выражается через координаты этих векторов и некоторые числа
выражается через координаты этих векторов и некоторые числа 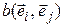 , которые с аргументами
, которые с аргументами 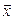 и
и 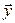 не связаны, а зависят только от выбранного базиса. Обозначим
не связаны, а зависят только от выбранного базиса. Обозначим
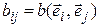 . (5.3)
. (5.3)
Из (5.2) вытекает
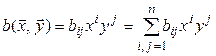 . (5.4)
. (5.4)
Равенство (5.4) называется координатной формой записи билинейной формы.
Определение. Матрицей билинейной формы 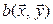 в базисе (5.1) называется матрица
в базисе (5.1) называется матрица 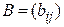 , где
, где 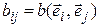 .
.
Обозначим, как обычно,
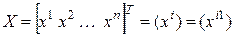 ,
,  –
–
координатные столбцы векторов 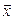 и
и 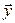 соответственно в заданном базисе. Заметим, что
соответственно в заданном базисе. Заметим, что 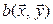 – число, которое можно рассматривать как матрицу размеров
– число, которое можно рассматривать как матрицу размеров 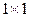 . В таком случае (5.4) можно переписать и так:
. В таком случае (5.4) можно переписать и так: 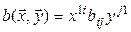 , откуда получаем
, откуда получаем
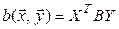 . (5.5)
. (5.5)
Это равенство называется матричной формой записи билинейной формы.
Итак, если в  задан базис, то каждой билинейной форме на линейном пространстве
задан базис, то каждой билинейной форме на линейном пространстве  соответствует единственная матрица В – матрица этой билинейной формы в заданном базисе. Докажем, что верно и обратное утверждение.
соответствует единственная матрица В – матрица этой билинейной формы в заданном базисе. Докажем, что верно и обратное утверждение.
Теорема 5.1. Пусть в линейном пространстве  задан какой-либо базис (5.1). Тогда для любой квадратной матрицы
задан какой-либо базис (5.1). Тогда для любой квадратной матрицы 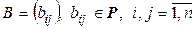 , на линейном пространстве
, на линейном пространстве  существует единственная билинейная форма
существует единственная билинейная форма 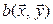 , матрица которой в заданном базисе совпадает с В, т. е. такая, для которой выполняется условие 5.3).
, матрица которой в заданном базисе совпадает с В, т. е. такая, для которой выполняется условие 5.3).
► Построение. Положим по определению:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
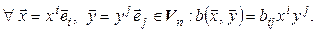
Линейность.
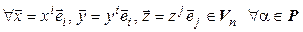 :
:
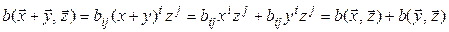 ;
;
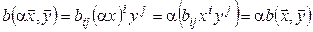 .
.
Таким образом, линейность 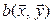 по первому аргументу доказана. Аналогично проверяется линейность и по второму аргументу.
по первому аргументу доказана. Аналогично проверяется линейность и по второму аргументу.
Выполнение условия (5.3). Так как 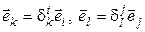 (т. е. i -я координата вектора
(т. е. i -я координата вектора 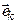 равна
равна 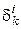 , а j- я координата вектора
, а j- я координата вектора 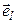 –
– 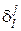 ), то
), то 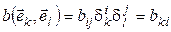 .
.
Единственность. Предположим, что существует еще одна билинейная форма 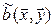 , не совпадающая с формой
, не совпадающая с формой  , для которой выполняется (5.3). Тогда
, для которой выполняется (5.3). Тогда
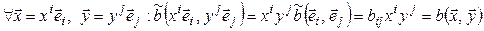 ,
,
и мы пришли к противоречию.◄
Таким образом, если в  задан какой-либо базис, то между множеством билинейных форм на линейном пространстве
задан какой-либо базис, то между множеством билинейных форм на линейном пространстве  и множеством квадратных матриц n -го порядка с элементами из поля Р устанавливается
и множеством квадратных матриц n -го порядка с элементами из поля Р устанавливается
взаимно однозначное соответствие.
|
|
