Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Изменение матрицы билинейной формы при изменении базиса
|
|
Теорема 5.2. Пусть в линейном пространстве 
заданы два базиса:
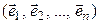(5.6)
и
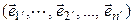, (5.7)
и пусть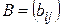 
и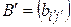 
– матрицы билинейной формы 
в базисах (5.6) и (5.7) соответственно. Тогда
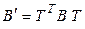, (5.8)
где Т – матрица перехода от (5.6) к (5.7).
► Воспользуемся определением билинейной формы и ее матрицы, а также определением матрицы перехода:
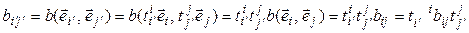. (5.9)
Заметим, что в правой части равенства (5.9) индекс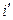 
должен соответствовать номеру строки, а индекс 
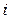– номеру столбца (по согласованию с левой частью), поэтому из (5.9) и вытекает равенство (5.8).◄
Следствие. Если матрица билинейной формы в одном из базисов пространства невырождена, то в любом другом базисе матрица этой билинейной формы также невырождена.
Определение. Билинейная форма на линейном пространстве называется невырожденной, если ее матрица в некотором, а значит, и в любом базисе пространства невырождена.
Определение. Квадратные матрицы 
и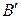 
называются конгруэнтными, если они связаны соотношением (5.8), где 
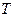– невырожденная матрица.
Таким образом, матрицы одной и той же билинейной формы в различных базисах конгруэнтны.
|
|