
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Зависимость скорости реакции от температуры
|
|
Для характеристики влияния температуры на скорость реакции для небольшого температурного интервала обычно используют температурный коэффициент (γ), представляющий собой отношение скоростей реакции или констант скорости реакции при двух температурах, отличающихся на 10º.
Правило Вант-Гоффа установлено экспериментально. Для гомогенных реакций:
γ = W Т+10 / W Т =2¸ 4 или γ = k Т+10 / k Т =2¸ 4
При повышении температуры на 10º константа скорости химической реакции увеличивается в 2-4 раза.
Химическая реакция, протекающая в пределах одной фазы, называется гомогенной химической реакцией (пример, любая реакция в растворе).
Химическая реакция, протекающая на границе раздела фаз, называется гетерогенной химической реакцией (пример, любая реакция, идущая на поверхности твердого катализатора - гетерогенная каталитическая реакция). Для гетерогенной реакции γ = 1, 1 ¸ 1, 3 (лимитирующей стадией является процесс диффузии).
Правило Вант-Гоффа является приближенным, так как температурный коэффициент принимают за постоянную величину. В действительности температурный коэффициент изменяется с температурой, при повышении температуры γ → 1.
Более точную зависимость влияния температуры на скорость химического процесса дает уравнение Аррениуса. Это основное уравнение химической кинетики:
dlnk/dT = E /RT2 - уравнение Аррениуса в дифференциальной. форме или
dlnk = E dT /RT2.
Проинтегрируем: lnk = - E/RT + const.
Пусть const = Н, тогда lnk = Н - E/ RT,
lnk = (Н - E/ RT)´ lne = lne(Н - E/ RT),
k = eH e(- E/ RT) = A e(- E/ RT).
Уравнение Аррениуса в интегральной форме.
k= A e - E/ RT,
где А - предэкспоненциальный множитель, который постоянен для данной реакции и данных условий (величина, практически не зависящая от температуры); е - основание натурального логарифма; Е - энергия активации.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Интегрирование уравнения Аррениуса в пределах температур Т1 и Т2 дает соотношение:
lnk2/k1 = (E/R)´ (1/T1 - 1/T2)
Перейдем к десятичному логарифму:
lgk2/k1 = (E/2, 303R)´ (1/T1 - 1/T2) = (E/2, 303R)´ (T2 - T1) / T1´ T2.
Зная энергию активации и хотя бы одно значение контакта скорости, можно рассчитать константу скорости для любой другой температуры.
5.6. Теории химической кинетики. Теория активных соударений
Задачи теорий химической кинетики: 1) выяснение механизма химических реакций; 2) выяснение влияния различных факторов на скорость реакции (температура, концентрация, давление, катализатор и др.); 3) теоретический расчет константы скорости.
Для теоретического расчета констант скоростей используют две теории: 1) теория активных соударений или теория бимолекулярных реакций Аррениуса (1889 г.); 2) метод активного комплекса или теория переходного состояния (Эйринг и Поляни, 1935 г). Эта теория сохранила значение и по настоящее время.
Теория активных соударений была предложена Аррениусом для бимолекулярных газовых реакций. Согласно кинетическим представлениям для начала реакции необходимо столкновение реагирующих молекул. Чем выше концентрация, тем больше число столкновений и тем больше скорость реакции: W = kc1´ c2. Однако опыт показывает, что реакция всегда протекает со значительно меньшей скоростью, т.е. столкновение молекул является необходимым условием, но не достаточным: не каждое столкновение приводит к реакции. Например, разложение йодистого водорода:
2HJ → H2 + J2.
Из 1017 столкновений лишь одно приводит к образованию продуктов реакции. Если скорость реакции зависит лишь от числа соударений, то нельзя объяснить влияние температуры на скорость реакции, так как при повышении температуры на 10º число столкновений увеличивается на 1-2 %, а скорость реакции возрастает в 2-4 раза.
По Аррениусу каждая химическая реакция протекает в две стадии:
нормальные молекулы «активные молекулы ® продукты реакции.
Аррениус принимал за активные молекулы особую химическую модификацию нормальных молекул. Аррениус не объяснил истинную природу активных молекул, физический смысл предэкспоненциального множителя “А” в уравнении: k = Ae -E/RT.
Дальнейшее развитие теории активных соударений было сделано Д.В. Алексеевым (1915-24 г.г.). Он предложил активными считать молекулы, обладающие повышенной энергией по сравнению со средней энергией молекул, и для объяснения природы активных молекул использовать законы Максвелла (закон распределения молекул по скоростям) и Больцмана (закон распределения молекул по энергиям). Закон Максвелла дает возможность определить, какая доля общего числа молекул в данных условиях обладает скоростью, точно отвечающей средней скорости, и какая отличается от нее на ту или другую заданную величину. В математической форме этот закон выражается сложным соотношением. Мы ограничимся здесь разбором только графического выражения этой зависимости (рис. 5.3.):
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
dN/Ndυ - доля молекул dN, обладающих скоростями в пределах между “W” и
“W + dW” от общего числа молекул N.
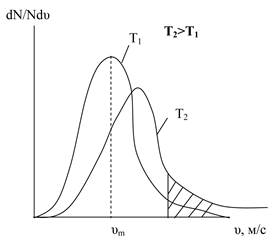
Рис. 5.3. Распределение молекул по скорости.
Кривые имеют четко выраженный максимум и сильнее растянуты в сторону больших скоростей. Скорость “W” называется наиболее вероятной, она не совпадает со средними скоростями. По Алексееву активные молекулы - это молекулы, располагающиеся в хвосте Максвелловской кривой, т.е. обладающие избыточной скоростью. Кривая распределения скоростей данного газа зависит только от температуры. При повышении температуры скорость молекул возрастает. Максвелловская кривая сдвигается вправо, одновременно уменьшается максимум, но доля молекул, обладающих избыточной скоростью резко возрастает (площадь, ограниченная кривой и осью “W”). Максвелловская кривая количественно описывается уравнением Больцмана. Для частного случая, когда энергия молекул зависит только от двух степеней свободы (движение в плоскости) уравнение имеет вид:
NE/N0 = e -E/RT,
где NE - число молекул с энергией не меньше “Е”, N0 - обще число молекул.
Такая же зависимость для числа двойных столкновений:
ZE/Z0 = e -E/RT.
Правый член (e -E/RT) - фактор Больцмана (фактор активации):
ZE = Z0·e -E/RT,
где ZE - число активных соударений, Z0 - общее число соударений.
С повышением температуры число активных соударений резко увеличивается. Основное положение теории активных соударений: реагируют лишь те молекулы, энергия которых в момент столкновения не ниже некоторого предела “Е”, называемого энергией активации.
Таким образом, энергией активации называется та минимальная избыточная энергия по сравнению со средней величиной, которой должны обладать молекулы, чтобы их столкновение привело бы к реакции.
Рассмотрим ход реакции в зависимости от энергетического состояния молекул (рис. 5.4.):
А + В↔ С + Д,
Е1 - энергия исходных веществ, Е2 - энергия продуктов реакции, Е3 - наименьший запас энергии, которым должны обладать молекулы, чтобы их столкновения могли привести к химическому взаимодействию.
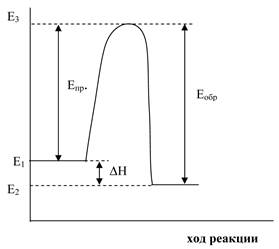
Рис. 5.4. Изменение энергии реакционной системы.
Данная реакция экзотермическая, т.е. общий запас энергии продуктов реакции меньше, чем исходных веществ: Δ Н = Е2 - Е1 < 0. Следовательно, по пути из исходного состояния в конечное состояние система должна перейти через энергетический барьер (Епр) и преодолеть его могут лишь активные молекулы, обладающие в момент столкновения необходимым избытком энергии.
Источниками активации молекул могут служить: 1) особо благоприятные столкновения, приводящие к перераспределению энергий молекул (для гомогенных газовых реакций); 2) действие внешних факторов (поглощение кванта света, электрический разряд, радиация и т.д.); 3) активация молекул исходных веществ, происходящая в процессе их активированной адсорбции поверхностными атомами катализатора (для гетерогенных каталитических реакций).
Энергия активации необходима для преодоления сил отталкивания при сближении молекул. Эти силы возникают за счет электростатического взаимодействия электронных оболочек молекул. Это приводит к увеличению потенциальной энергии системы и выражается в разрыхлении химических связей реагирующих молекул. Энергия активации складывается: 1) из повышения энергии поступательного и вращательного движения молекул, 2) из повышения энергии колебания атомов и атомных групп в молекуле, 3) из повышения энергии движения электронов.
Скорость реакции и число активных соударений связано с общим числом соударений следующим уравнением:
W= ZE = Z0·e -E/RT.
Для многих реакций υ < ZE. Почему? Причины:
1. Необходимо чтобы молекулы столкнулись по реакционному центру:
W= p·ZE = p·Z0·e -E/RT,
где p - стерический коэффициент (фактор вероятности). Значение “p” меняется в пределах от 1 до 10-9 и теоретически не может быть рассчитано. Все это следствие несовершенства и формального характера теории активных соударений, которая рассматривает молекулы реагирующих веществ как жесткие шарики.
Например, реакция этерификации замещенных бензойных кислот в присутствии концентрированной минеральной кислоты:
R-Ph-СOOH + C2H5OH ® сложный эфир.
При R=Н реакция протекает легко. Если в орто-положение к карбоксильной группе ввести заместитель (R = NO2), то реакция вообще не пойдет. Скорость реакции понижается в ряду R = F, Br, Cl, J.
2. Для сильно экзотермических реакций выделяющаяся энергия может привести к распаду продуктов реакции на исходные вещества.
3. При слишком кратковременных соударениях сложных молекул энергия не успевает перераспределиться должным образом и привести к разрыву нужных связей.
|
|
