💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

nbsp; 6. Прямой алгоритм с искусственными переменными

1. Рассмотрим теперь прямой алгоритм симплексно­го метода для случая, когда каноническая форма полу­чается путем введения в уравнения системы искусствен­ных переменных. Предварительно исходную систему уравнений преобразуем так, чтобы все свободные члены b_j были неотрицательны. Пусть дана задача линейного программирования в стандартной форме:

найти

x_j ³ 0 (j =1, 2, …, n) (6.1)

при условиях

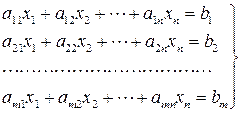(6.2)

c₁x₁ + c₂x₂ + ··· c_nx_n = z à min (6.3)

Введем в уравнение системы (6.2) базисное множество искусственных переменных x_n+i ≥ 0 (i = 1, 2, …, m). Кро­ме того, в целевой функции перенесем z в левую часть со знаком минус и, таким образом, приравняем (6.3) нулю; получим расширенную систему уравнений;

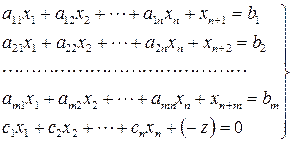(6.4)

и

x_j ³ 0 (j =1, 2, …, n, n+1, …, n+m) (6.5)

Сумму искусственных переменных (обозначим ее че­рез u)

x_n+1 + x_n+2 + ··· + x_n+m = u (6.6)

будем называть, искусственной линейной формой (или u -уравнением).

Исключим переменные x_n+1, x_n+2, …, x_n+m из u -уравнения, вычитая из него сумму первых m уравнений рас­ширенной системы (иначе говоря, находим значения искусственных переменных из уравнений расширенной системы и подставляем их в искусственную форму). Тогда коэффициенты при x₁, x₂, …, x_n будут соответст­венно равны: d₁ = –(a₁₁ + a₁₂ +…+ a_m1), d₂ = –(a₁₂ + a₂₂ +…+ a_m2), …, d_j = –(a_1j + a_2j +…+ a_mj), …, d_n = –(a_1n + a_2n +…+ a_mn). Перенесем u в левую часть (со знаком минус), а свободный член — в правую часть с обратным знаком; будем иметь:

d₁x₁ + d₂x₂ +···+ d_nx_n + u₀ = u, где

u₀=b₁+b₂+···b_m,

или d₁x₁ + d₂x₂ +···+ d_nx_n +(- u)= u₀ (6.7)

Добавив к расширенной системе уравнений (6.4) пре­образованное u -уравнение (искусственную форму), по­лучим следующую каноническую форму:

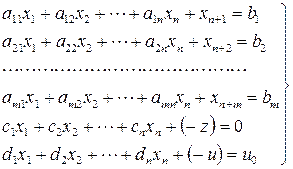(6.8)

Используем алгоритм, описанный в пп. 1, 2, 3 описания прямого симплекс-метода, для получения решения системы (6.4)–(6.5), которое дает минимальное значение u.

Составим начальную таблицу 2 по аналогии с ра­нее составлявшейся таблице с той лишь разницей, что дополняем, её еще одной стро­кой, в клетки которой вписываем коэффициенты d_j u- уравнения (6.7). Таким образом, первоначальную табли­цу 2 заполняем соответствующими коэффициентами канонической формы (6.8), при этом в клетках, относя­щихся к базисным переменным, нули писать не будем.

2. Пусть дана стандартная форма задачи линейного программирования (в сокращенной записи):

найти

x_j ³ 0 (j =1, 2, …, n) (6.9)

при условиях

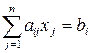(i =1, 2, …, m), (6.10)

дающих

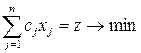, (6.11)

при этом

b_i ³ 0 (i =1, 2, …, m). (6.12)

Введем искусственные переменные х_n+j, связанные с x₁, x₂, …, x_n; получим расширенную систему:

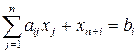(i =1, 2, …, m), (6.13)

, (6.14)

x_j ³ 0 (j =1, 2, …, n, n+1, …, n+m). (6.15)

Как было принято, искусственная линейная форма (сумма искусственных переменных) есть

x_n+1+ x_n+2+ … + x_n+m=u (6.16)

Теперь задача состоит в том, чтобы найти минималь­ное значение u. Для этого используем алгоритм, описан­ный в описании прямого симплекс-метода, чтобы получить решение системы (6.13)—(6.15), которое дает минимальное значение искусственной линейной формы u. При условии x_n+1 =0, x_n+2 =0, …, x_n+m =0 очевидно, решение системы (13) эквивалентно системе (10).

В системе (6.13) искусственные переменные x_n+i (i =l, 2, …, m) образуют базис. Путем преобразований указанной системы искусственные базисные переменные x_n+i будут переходить в число небазисных переменных, а последние вводятся в базис вместо искусственных переменных. Переход от одного базиса к другому на не­которой итерации приведет к тому, что базис не будет содержать ни одной искусственной переменной. Этот переход осуществляется путем применения указанного алгоритма; при этом решается задача о минимизации u.

Действительно, указанный алгоритм можно приме­нить, поскольку расширенная система представляет ка­ноническую форму с базисом (x_n+1, x_n+2, …, x_n+m). Чёрез некоторое число итераций соответствующее базисное решение даст min u. При этом минимальное значение целевой функции может быть или положительным, или равным нулю, так как u есть сумма неотрицательных переменных. В самом деле, так как u≥ 0, то и min u≥ 0.

В случае если окажется min u > 0, то задача не име­ет допустимого решения. В самом деле, поскольку система (6.13)—(6.14) не имеет неотрицательных решений, для которых x_n+1 =0, x_n+2 =0, …, x_n+m =0 (тогда min u =0 ), то и исходная система также не имеет неотрицательных решений, и процесс решения на этом заканчивается.

Если min u =0, то для минимального значения u ре­шение будет (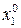, , 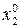…, , , 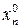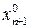…, 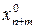), так как из условия 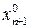+ +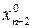…+ 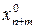=min u =0 следует 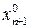=0, 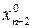=0, …, 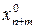=0. Следовательно, (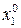, , 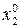…, 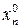) есть неотрицательное решение исходной формы системы, при этом среди компонент 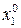, , 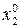…, 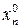не более m отличных от нуля. Решение начинаем следую­щим образом:

исключаем из дальнейшего рассмотрения все не базисные переменные, соответствующие u -строке табли­цы 2 положительным (не нулевым) коэффициентам d_j;

заменяем искусственную форму и линейной формой z, которая получается после исключения из u -строки всех базисных переменных.

Отметим, что искусственную переменную, исключен­ную из базиса в результате некоторой итерации, не сле­дует в дальнейшем вводить ни в один из последующих базисов; поэтому нет необходимости делать преобразо­вания последних m столбцов.

Таким образом, вычисления начинаем с расширенной задачи. После того как выяснится, что в u -строке таб­лицы достигнут min=0, приходим к решению исходной задачи.

Решение задачи линейного программирования пря­мым алгоритмом симплексного метода с введением в ее стандартную форму искусственных переменных нагляд­но показано в блок-схеме 2.

Блок-схема 2

Алгоритм прямого (с искусственными переменными) симплекс-метода.

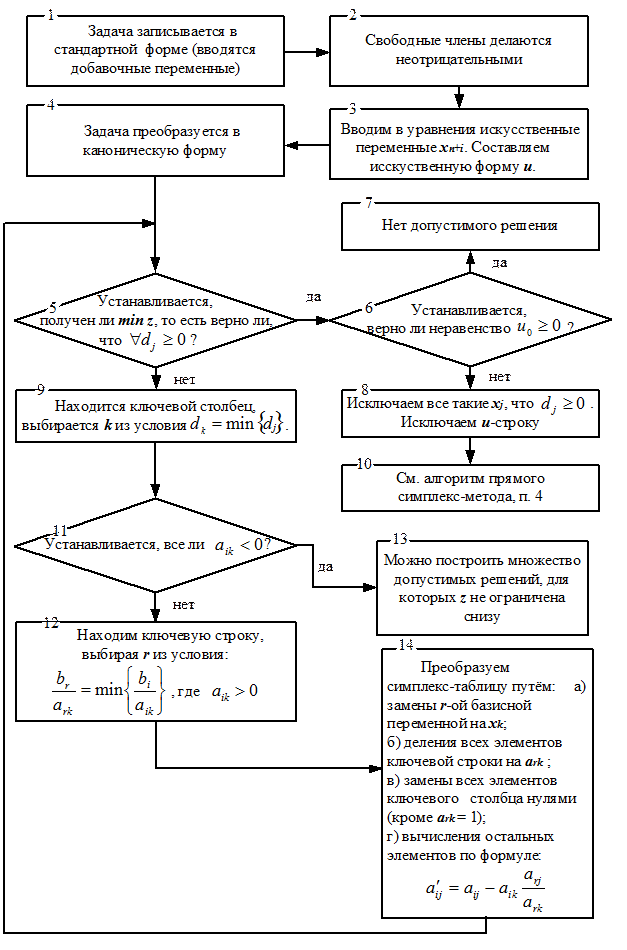
Таблица 2

Симплекс-таблица (исходная).

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.

1. Горстко А. Б. Познакомьтесь с математическим моделированием.

- М.: Знание, 1991. – 160 с.: ил.

2. Вершинин О. Е. Компьютер для менеджера: Уч. пособие.

- М.: Высш. школа, 1990. – 240 с.: ил.

3. Ромакин М. И. Математический аппарат оптимизационных задач.

- М.: Статистика, 1975.

4. Щедрин Н. И., Кархов А. Н. Математические методы программирования в экономике. – М.: Статистика, 1974.

5. Конторович Л. В., Горстко А. В. Оптимальные решения в экономике. - М.: Наука, 1972.