
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Симплекс-метод. Анализ процедуры решения задачи линейного программирования (с примером).
|
|
Рассмотрим вычислительные и логические процедуры, обеспечивающие поиск решения задачи линейного программирования симплекс-методом. Процедуры поясняются в процессе решения конкретной задачи: найти совокупность значений  , удовлетворяющих системе неравенств:
, удовлетворяющих системе неравенств:
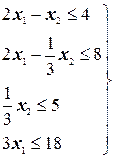 (3.1)
(3.1)
и условиям неотрицательности переменных 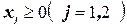 , для которых
, для которых
целевая функция
z=10+7x1-5/3x2 (3.2)
достигает максимума.
Преобразуем заданную форму задачи в каноническую, введя дополнительные переменные 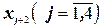 . Получим систему линейных уравнений (здесь дополнительные переменные составляют единичный базис):
. Получим систему линейных уравнений (здесь дополнительные переменные составляют единичный базис):
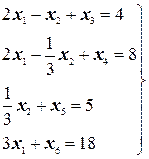 (3.3)
(3.3)
и форму z: 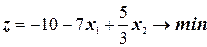 (3.4)
(3.4)
Выберем в качестве свободных (независимых) переменных 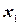 и
и 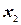 , так как через них выражена линейная форма; переменные
, так как через них выражена линейная форма; переменные 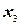 ,
, 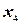 ,
, 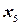 ,
, 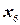 - базисные. Так как все величины
- базисные. Так как все величины 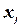 должны быть неотрицательны, то их наименьшие значения равны нулю:
должны быть неотрицательны, то их наименьшие значения равны нулю: 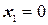 ,
, 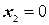 . Подставив эти значения в систему, получим следующие значения несвободных (базисных) переменных:
. Подставив эти значения в систему, получим следующие значения несвободных (базисных) переменных: 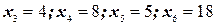 . Эти значения также положительны, поэтому система значений
. Эти значения также положительны, поэтому система значений 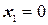 ;
; 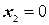 ;
; 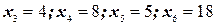 образует допустимое базисное решение системы (3.3). При найденном решении значение z оказывается равным «-10».
образует допустимое базисное решение системы (3.3). При найденном решении значение z оказывается равным «-10».
Выше были приняты значения свободных переменных равными нулю (наименьшими при условии их неотрицательности). Попробуем за счёт их увеличения добиться уменьшения формы z.
Из выражения целевой функции видно, что, так как 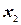 входит в неё со знаком плюс, то её увеличение может привести только к увеличению значения z. Неизвестная
входит в неё со знаком плюс, то её увеличение может привести только к увеличению значения z. Неизвестная 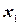 входит в неё со знаком минус, поэтому её увеличение «выгодно». Однако неограниченное увеличение этой свободной неизвестной может привести к отрицательности несвободных (базисных) неизвестных, то есть привести к недопустимому решению. Так, из первого уравнения видно, что, если
входит в неё со знаком минус, поэтому её увеличение «выгодно». Однако неограниченное увеличение этой свободной неизвестной может привести к отрицательности несвободных (базисных) неизвестных, то есть привести к недопустимому решению. Так, из первого уравнения видно, что, если 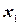 станет больше двух (
станет больше двух (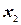 остаётся свободной и равной нулю), то
остаётся свободной и равной нулю), то 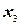 станет отрицательной. Таким образом, при
станет отрицательной. Таким образом, при 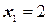 ,
, 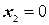 остальные переменные примут значения:
остальные переменные примут значения: 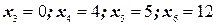 , следовательно, получаем новое допустимое базисное решение. Теперь свободными стали
, следовательно, получаем новое допустимое базисное решение. Теперь свободными стали 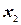 и
и 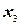 ; остальные – базисными. Проведя преобразования (выразив ограничения и линейную форму через новые свободные переменные) получим:
; остальные – базисными. Проведя преобразования (выразив ограничения и линейную форму через новые свободные переменные) получим:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
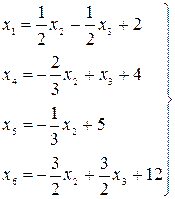 (3.5)
(3.5)
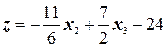 (3.6)
(3.6)
Соответствующее допустимое базисное решение:
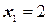 ;
; 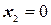 ;
; 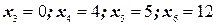
Проведя аналогичные рассуждения, принимая во внимание, что 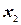 входит в целевую функцию со знаком минус, на основе второго уравнения из системы (3.5) увеличиваем
входит в целевую функцию со знаком минус, на основе второго уравнения из системы (3.5) увеличиваем 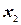 до значения
до значения 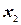 = 6. При этом происходит ввод переменной
= 6. При этом происходит ввод переменной 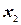 в базис и вывод из него
в базис и вывод из него 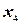 в качестве свободной. Получаем:
в качестве свободной. Получаем:
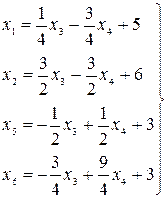 (3.7)
(3.7)
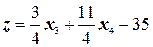 (3.8)
(3.8)
Теперь свободные неизвестные входят в выражение линейной формы со знаком плюс. Их увеличение может привести только к увеличению формы. Следовательно, базисное решение, являющееся оптимальным, имеет вид:
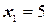 ;
; 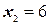 ;
; 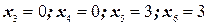 ,
,
минимальное значение формы: 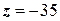 , а максимальное значение
, а максимальное значение 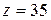 .
.
Таким образом, идея симплекс-метода преобразования модели заключается в таком итеративном направленном переходе от одного допустимого базисного решения к другому, при котором последовательно улучшается значение линейной формы.
|
|
