Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Графический метод решения задач.

Проиллюстрируем проведенные этапы графическим методом решения задач, заданных в канонической форме при наличии не более двух свободных переменных. Обратимся к системе (3.1) и форме (3.2).

На рис. 4.1 представлен многоугольник решений и линейная форма. Здесь совокупность независимых переменных – это система координат. Линейная форма z в точке 0 даёт одно из допустимых базисных решений. Проведение преобразований – выбор новой пары свободных переменных (вместо 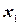, 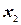- пара 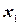, 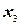) – означает переход к новой системе координат. Причём видно, что движение по оси 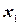возможно только до значения 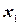=2. Так как каждое уравнение в пространстве представляет из себя гиперплоскость (у нас прямая линия), то движемся по оси 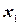до встречи с новой гиперплоскостью (прямой), то есть пока 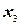не станет равной нулю. Точка 0¢ соответствует новому началу координат с осями , .

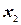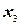Новый вид задачи представлен на рис. 4.2. Здесь целевая функция в точке 0¢ опять даёт одно из допустимых базисных решений. Следующее преобразование системы координат – движение по оси 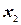до величины 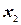=6 (точка 0¢ ¢) – переход к системе 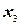, 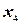(рис. 4.3).

Из рис. 4.3 видно, что целевая функция при своём перемещении в направлении вектора 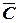достигает точки 0¢ ¢. Допустимое базисное решение в этом случае является и оптимальным (напомним, что линейная форма достигает минимума или максимума только в вершине многогранника решений).

Таким образом, графически (для плоской задачи) симплекс-метод обуславливает переход от одной системы координат к другой, причём заменяемая ось входит в выражение z с отрицательным коэффициентом, то есть z отсекает у неё отрезок в направлении отрицательной полуоси. Процесс происходит до тех пор, пока целевая функция не будет отсекать отрезки у одноимённых по знаку полуосей. Тогда минимум будет достигнут в начале координат.

Рис. 4.1.

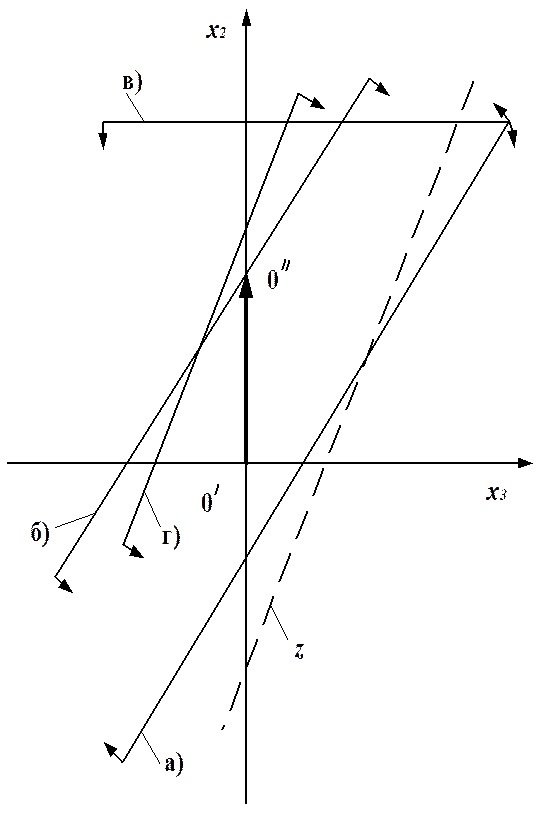Рис. 4.2.

ЗАМЕЧАНИЯ.

Отметим некоторые закономерности, которые могут быть полезны при рассмотрении алгоритма прямого симплекс-метода.

1. Проводя первый этап преобразований системы 3.1, мы увеличиваем 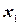до двух, что очевидно из рис. 4.1. Из этого же рисунка видно, что можно было «надеяться» на встречу также с прямыми б) и г), так как в соответствующих им уравнениям коэффициенты при 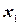положительны. Однако первой встретилась прямая а), для которой выполняется условие:

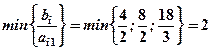(4.1)

2. Предположим, что система (3.3) и функция (3.4) имели бы вид:

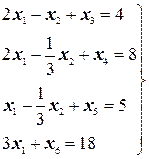(4.2)

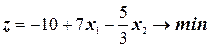(4.3)

тогда из рис. 4.4 видно, что необходимое движение по оси 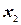может продолжаться бесконечно. Аналитически это соответствует сочетанию условий: коэффициенты при соответствующих переменных в целевой функции и в уравнениях отрицательны.

Рис. 4.4.