
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямой алгоритм симплексного метода
|
|
1. Рассмотрим прямой алгоритм симплексного метода, в котором используется рассмотренный математический аппарат, имея в виду при этом представление задачи линейного программирования в канонической форме.
Задача линейного программирования может быть представлена в канонической форме следующим образом:
с помощью элементарных преобразований,
в результате преобразования в уравнения исходных ограничений, имеющих неравенства вида £ («меньше или равно»),
путем введения в уравнения системы некоторых искусственных переменных.
Пусть задача линейного программирования представлена в канонической форме в следующем виде:
найти
xj ³ 0 (j =1, 2, …, p, p +1, …, p + m) (5.1)
при условиях
 (5.2)
(5.2)
c1x1 + c2x2 + ··· + cpxp + cp+1xp+1 + ··· + cp+mxp+m = z à min (5.3)
В такой постановке задачи исходные уравнения системы (5.2) содержат в числе других также m переменных xp+1, xp+2, …, xp+m, при которых коэффициенты образуют единичную матрицу, или базис. Отметим, что порядковые номера базисных переменных здесь не играют роли; важно, чтобы каждая из таких переменных входила лишь в одно уравнение, причем с коэффициентом (+1).
В целевую функцию переменная может входить с любым коэффициентом (положительным, отрицательным или нулевым).
Для подготовки задачи к ее решению по прямому алгоритму выразим целевую функцию z через небазисные переменные. Для этого значения xp+1, xp+2, …, xp+m, полученные соответственно из первого, второго, …, последнего уравнения системы (5.2), подставим в целевую функцию. Затем целевую функцию запишем в виде уравнения, перенеся z (со знаком минус) в одну часть вместе с переменными xj, а свободный член c0' (с обратным знаком) — в другую. Будем называть это уравнение целевым уравнением или z -строкой. Тогда задача будет представлена в следующем виде:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
xj ³ 0 (j =1, 2, …, p, p +1, …, p + m) (5.1)
удовлетворяющее соотношениям
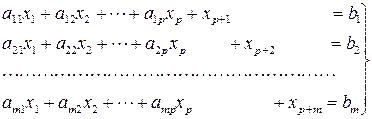 (5.2)
(5.2)
c'1x1 + c'2x2 + ·· ·+ c'pxp + (— z) = — c'0 (5.3')
Систему уравнений (5.2) — (5.3') будем называть представленной в полной канонической форме, в которой, кроме базисных переменных xp+1, xp+2, …, xp+m, переменную (— z) будем принимать также за базисную. [Учитывая, что базисные переменные принимаются с коэффициентами (+1) можно (— z) представить в виде, например, xz ].
Для полной канонической формы базисным решением будет следующее: x1= 0, х2= 0, …, xр= 0, xp+1=b1, xр+2=b2, …, xр+m=bm, z=c'0, котороё принимается в качестве первоначального решения задачи. Поскольку каноническая форма вытекает из стандартной, а в последней свободные члены сделаны положительными величинами, будем говорить, что задача представлена в допустимой канонической форме.
2. Как только что было установлено, каноническая форма позволяет непосредственно найти соответствующее базисное допустимое решение. Каноническую форму можно использовать также для выяснения, будет ли допустимое базисное решение минимальным, для чего коэффициенты c'j (j = 1, 2, …, р) целевого уравнения проверяются на оптимальность. Коэффициенты с'j будем называть относительными оценками, так как их значения зависят от выбора базисного множества переменных. Отмеченное выше основывается на следующих предложениях о критерии оптимальности:
А. Базисное допустимое решение является минимальным допустимым решением со значением z=c'0, если все относительные оценки неотрицательны:
c'j ³ 0(j = 1, 2, …, р)
Действительно, для канонической формы очевидно, что если все коэффициенты целевого уравнения неотрицательны, то наименьшая величина суммы c'1x1 + c'2x2 + ··· + c'pxp + c'p+1xp+1 + ··· + c'p+mxp+m есть нуль при любом выборе неотрицательных xj. Следовательно, наименьшая величина разности (z – c'0) равна нулю и min z ³ c'0. В частности, для допустимого базисного решения z=c'0; поэтому min z ³ c'0, и решение оптимально. Очевидно также следующее другое предложение.
Б. Пусть дано минимальное допустимое базисное решение с относительными оценками с'j ³ 0; тогда любое другое допустимое решение (не обязательно базисное) при xj= 0 для всех c'j > 0 также является минимальным решением. Если же это решение обладает тем свойством, что для некоторого j как xj > 0, так и c'j > 0, то оно не может быть минимальным решением.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
В. Базисное допустимое решение является минимальным допустимым решением, если c'j > 0 для всех небазисных переменных.
3. В п. 1 нами получено первоначальное решение линейной задачи (в общем виде), которое является базисным допустимым решением. Теперь перейдем к другому базисному допустимому решению, улучшив последнее.
Для описания вычислительного процесса будем пользоваться так называемыми симплексными таблицами, причем переход от одной таблицы к другой будет соответствовать одной итерации.
В начале каждой итерации исследуем по критерию оптимальности базисное допустимое решение и, если оно не оказалось оптимальным и при этом не выявлена неразрешимость задачи, преобразуем таблицу (по правилам, о которых скажем далее) так, что это приводит к новому допустимому базисному решению, с меньшим значением целевой функции (во всяком случае, не большим). Для этого прежде всего определяется вектор, который должен быть введен в базис, и вектор, который должен быть выведен из базиса. (Для краткости иногда вместо вектора мы будем называть переменную, соответствующую этому вектору.)
В первом столбце таблицы 1 записаны базисные переменные, а также базисная переменная (– z). В следующих столбцах пишем коэффициенты при переменных в полной канонической системе. В последнем столбце – свободные члены (компоненты вектора В). В последней строке записаны коэффициенты сj, из линейной формы (целевой функции).
Первая (исходная) таблица 1 имеет следующий вид:
Таблица 1
Симплекс-таблица (исходная).
| Базисн. перем. | x1 | … | xj | … | xk | … | xp | xp+1 | … | xp+i | … | xp+m | Свободн. члены |
| xp+1 | a11 | … | a1j | … | a1k | … | a1p | 1 | … | 0 | … | 0 | b1 |
| xp+2 | a21 | … | a2j | … | a2k | … | a2p | 0 | … | 0 | … | 0 | b2 |
| … | |||||||||||||
| xp+i | ai1 | … | aij | … | aik | … | aip | 0 | … | 1 | … | 0 | bi |
| … | |||||||||||||
| xp+r | ar1 | … | arj | … | ark | … | arp | 0 | … | 0 | … | 0 | br |
| … | |||||||||||||
| xp+m | am1 | … | amj | … | amk | … | amp | 0 | … | 0 | … | 1 | bm |
| (-z) | c¢ 1 | … | c¢ j | … | c¢ k | … | c¢ p | 0 | … | 0 | … | 0 | c¢ 0 |
А. Первым шагом в анализе первоначального допустимого базисного решения является проверка его на оптимальность. Она заключается в отыскании в последней z -строке максимального по модулю отрицательного коэффициента. Столбец c максимальным по модулю отрицательным коэффициентом (пусть это будет с'k) назовём ключевым, а переменная этого столбца xk будет новой базисной переменной, которая вводится в базис. В случае если окажется несколько равных по модулю отрицательных коэффициентов, то можно выбрать любой из них.
Если в z -строке отрицательных чисел нет, то получено минимальное (оптимальное) решение.
Б. Далее устанавливаем, какая переменная будет выведена из базиса. Для этого составляем отношения свободных членов к соответствующим положительным числам ключевого столбца  , …,
, …, 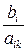 , …,
, …, 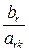 , …,
, …, 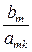 и выбираем наименьшее из этих отношений, т. е.
и выбираем наименьшее из этих отношений, т. е.
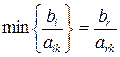 (aik > 0, ark > 0).
(aik > 0, ark > 0).
Выбранную с таким наименьшим отношением строку называем ключевой, а базисную переменную xr этой строки выводим из базиса и заменяем переменной xk ключевого столбца.
Элемент, стоящий на пересечении ключевого столбца и ключевой строки, будем называть ключевым элементом.
В литературе по линейному программированию ключевые столбцы и строки называются также направляющими, ведущими, разрешающими, а элемент, стоящий на их пересечении, —соответственно направляющим, ведущим, разрешающим.
В случае если окажется несколько равных отношений 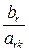 , то рекомендуется выбрать отношение с максимальным знаменателем.
, то рекомендуется выбрать отношение с максимальным знаменателем.
В. Переходим к построению следующей таблицы. В этой таблице прежде всего заполняются клетки строки xr с вводимой переменной хk. Для этого все элементы ключевой строки делятся на ключевой элемент; таким образом, xr -уравнение разрешается относительно хk. Получаем следующие элементы строки:
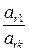 ,
, 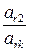 , …,
, …, 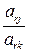 , …, 1, …,
, …, 1, …,  , 0, …,
, 0, …, 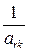 , …, 0,
, …, 0, 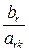 .
.
С помощью элементарных преобразований системы уравнений можно, как известно, любую переменную исключить из всех уравнений системы, кроме какого-либо одного. В данном случае нам необходимо исключить переменную хk из всех уравнений (строк), кроме одного (ключевой строки). Чтобы исключить хk из всех уравнений системы, надо, чтобы в клетках ключевого столбца (кроме ключевого элемента аrk =1) на месте элементов а1k, а2k, …, а r-1; k, а r+1; k, …, аmk были нули. Это достигается следующим образом. Пусть мы хотим исключить переменную хk из i -гo уравнения. Для этого достаточно уравнение с ключевым элементом аrk =1 умножить на (– аik) и прибавить к i -му уравнению. После исключения хk из всех уравнений система уравнений преобразуется в эквивалентную ей систему.
Остальные элементы таблицы (коэффициенты при переменных и свободные члены) будут связаны с коэффициентами при переменных и свободными членами исходной системы так называемыми формулами исключения;
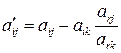 (i
(i 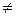 r, ark > 0),
r, ark > 0),
 (i
(i 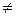 r, ark > 0).
r, ark > 0).
Эти формулы легко запомнить, если посмотреть на прямоугольник в таблице 1, в вершины которого поместить, например, элементы, входящие в формулу исключения (эти элементы выделены в таблице 1). Для того чтобы найти элемент  , который будет стоять в клетке новой таблицы на месте элемента aij надо из последнего вычесть произведение элементов (aik · arj), стоящих в вершинах побочной диагонали, и разделить на элемент аrk, стоящий по главной диагонали. Указанное правило относится и к нахождению свободных членов. Преобразованные по формулам исключения элементы записываем в соответствующие клетки новой таблицы. Для практических расчетов следует иметь в виду следующее:
, который будет стоять в клетке новой таблицы на месте элемента aij надо из последнего вычесть произведение элементов (aik · arj), стоящих в вершинах побочной диагонали, и разделить на элемент аrk, стоящий по главной диагонали. Указанное правило относится и к нахождению свободных членов. Преобразованные по формулам исключения элементы записываем в соответствующие клетки новой таблицы. Для практических расчетов следует иметь в виду следующее:
в новой таблице на месте ключевого элемента пишем 1, а на месте остальных элементов ключевого столбца— нули;
если в ключевой строке (старой таблицы) окажется нуль, то соответствующий ему столбец переписываем в новой таблице без изменения;
если в ключевом столбце окажется нуль, то соответствующую ему строку перепишем в новой таблице без изменения.
Отметим, что для нахождения элементов z -строки используем те же формулы исключения.
Г. После того как составлена вторая симплексная таблица, просматриваем в ней z -строку, чтобы выявить, получено ли оптимальное (минимальное) решение с помощью критерия оптимальности. Если все элементы этой строки (соответствующие небазисным переменным) окажутся положительными или равными нулю, то получено оптимальное решение (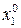 ,
, 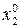 , …, хk, …,
, …, хk, …, 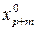 ), для которого имеем min z.
), для которого имеем min z.
Если в z -строке окажутся отрицательные элементы, то выбираем наименьший из них; соответствующий этой относительной оценке столбец будет ключевым, а переменная этого столбца будет базисной переменной, которая и вводится в новый базис.
Затем устанавливаем, какая переменная будет выведена из базиса (по правилу, указанному в п. Б). Далее переходим к построению новой симплексной таблицы (по правилу, указанному в п. В), по z -строке которой устанавливаем, получено ли оптимальное (минимальное) базисное решение, т. е. исследуем на оптимальность допустимое базисное решение.
Переход от одной таблицы к другой повторяется до тех пор, пока не будет получено оптимальное решение или не будет выявлено (в случае, если окажется, что относительная оценка ключевого столбца отрицательна, а все его элементы неположительны), что можно построить множество допустимых решений, для которых z не ограничено снизу.
Рассмотренный нами вычислительный процесс с помощью прямого алгоритма симплексного метода можно наглядно показать на блок-схеме 1.
Отметим, что если некоторой переменной, не входящей в конечный базис, в z -строке соответствует относительная оценка, равная нулю, то эту переменную можно обычным образом ввести в базис и получить новое решение, которое будет также оптимальным. При наличии двух (или более) оптимальных решений любые их выпуклые комбинации будут оптимальными.
Блок-схема 1
Алгоритм прямого симплекс-метода.
|
|
