Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Задача №7. а) побудувати епюри точок зображених на просторовій моделі системи площин проекцій;

Для наданого рисунка:

а) побудувати епюри точок зображених на просторовій моделі системи площин проекцій;

б) записати координати побудованих точок;

в) знайти точки(у), найбільш віддалені від площини проекцій Π ₁;

г) знайти точки(у), найбільш віддалені від площини проекцій Π ₂;

д) знайти точки(у), найбільш віддалені від площини проекцій Π ₃;

е) визначити, чи є точки, що рівновіддалені від однієї площини проекцій.

1.2 Пряма. Взаємне положення прямих

Відомо, що пряма лінія ℓ в просторі визначається положенням двох її точок, наприклад А і В, які показані на рис. 1.5. Це означає, що достатньо виконати комплексне креслення вказаних точок, з’єднати однойменні проекції точок прямими лініями та отримати відповідно горизонтальну А1В1, фронтальну А2В2, профільну А3В3 проекції прямої, заданої відрізком AB (див. рис.1.5).

Рисунок 1.5 – Утворення прямокутних

проекцій прямої лінії

Відносно площин проекцій пряма може займати різне положення. Пряма, яка не паралельна жодній з площин проекцій має назву прямої загального положення. Комплексне креслення такої прямої показано на рис. 1.6.

Пряму, паралельну одній з площин проекцій, називають прямою рівня. Пряму, перпендикулярну одній з площин проекцій, називають проекціювальною прямою.

Рисунок 1.6 - Комплексне креслення

прямої загального положення

Точки, в яких пряма перетинає площини проекцій, називають слідами. На рис. 1.7 показано пряму загального положення, яка утворена двома точками N і M, кожна з яких належить відповідній площині проекцій. Тому сліди прямої лінії можна розглядати як точки, які одночасно належать прямій та площині проекцій.

Рисунок 1.7 - Сліди прямої загального положення

Пряма загального положення перетинає три площини проекцій, тому має три сліди.

Пряма рівня перетинає дві площини проекцій. На рис. 1.8 показано побудову слідів горизонтальної прямої АВ. Точка M (M1, M2) – фронтальний слід прямої, точка N (N1, N3)- профільний слід прямої.

Рисунок 1.8 - Сліди прямої рівня

Проекціювальна пряма перетинає одну площину проекцій. На рис.1.9 показано побудову сліду фронтально-проекціювальної прямої АВ. Точка M (M1, M2) – фронтальний слід прямої АВ, або точка, яка одночасно належить площині проекції Π 2 та прямій.

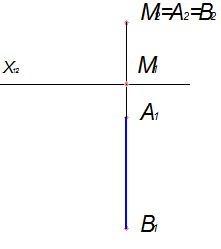
Рисунок 1.9 - Слід проекціювальної прямої

Дві прямі в просторі можуть перетинатись, бути паралельними та мимобіжними.

Якщо дві прямі a і b перетинаються в деякій точці А (показано на рис. 1.10), то проекції цієї точки повинні належати однойменним проекціям прямих, тобто точки перетину однойменних проекцій прямих, що перетинаються, повинні належати одній лінії зв’язку А1А2.

Рисунок 1.10 - Утворення прямокутних

проекцій прямих, що перетинаються

Якщо дві прямі a і b паралельні (показано на рис. 1.11), то на комплексному кресленні їх однойменні проекції також паралельні a2//b2, a1//b1.

Рисунок 1.11 - Утворення прямокутних проекцій паралельних прямих

Якщо дві прямі a і b мимобіжні, то на комплексному кресленні їх однойменні проекції перетинаються в точках, що не належать одній лінії зв’язку. На рис. 1.12 горизонтальні проекції прямих а1 і b1 перетинаються в точці А1=В1, яка відповідає горизонтальній проекції двох конкуруючих відносно площини проекцій Π 1 точок А і В, а фронтальні проекції прямих а2 і b2 перетинаються в точці C2=D2, яка відповідає фронтальній проекції двох конкуруючих відносно площини проекцій Π 2 точок C і D.

Рисунок 1.12 - Утворення прямокутних

проекцій мимобіжних прямих

Задачі для самостійного розв’язування