Багатогранники

3.1 Прямокутні проекції багатогранників

За допомогою непохідної фігури – площини можна обмежити будь-яку фігуру тривимірного простору. Фігуру, що утворилася при цьому називають багатогранником. Якщо площини замикають простір з усіх боків, то вони формують замкнений багатогранник. Елементами такого багатогранника є грані, ребра та вершини:

- грані – багатокутники, що складають гранну поверхню;

- ребра – сторони багатокутників;

- вершини – точки перетину ребер.

Сукупність всіх вершин та ребер багатогранника має назву його сітки.

З усіх багатогранників практичний інтерес становлять перш за все показані на рис. 3.1 призми, піраміди та їх різновиди.

Багатогранник, дві грані якого n-кутники, що знаходяться у паралельних площинах, а інші n граней – паралелограми, називають n-кутною призмою. Вказані багатокутники називають основами призми, паралелограми – бічними гранями (див. рис. 3.1, а).

Багатогранник, одна з граней якого – довільний багатокутник, а інші грані – трикутники, що мають спільну вершину, називають пірамідою. Грань-багатокутник прийнято називати її основою, грані-трикутники – бічними гранями. Спільна вершина трикутників має назву особливої вершини (зазвичай, просто вершини) піраміди (див. рис. 3.1, б).

Багатогранник, вершинами якого є вершини основи піраміди та вершини його перерізу площиною, має назву зрізаної піраміди. Очевидно, зрізана піраміда з невласною особливою вершиною є призмою.

На рис. 3.1, г показано один з різновидів багатогранника, складовими якого є зрізана піраміда та призма.

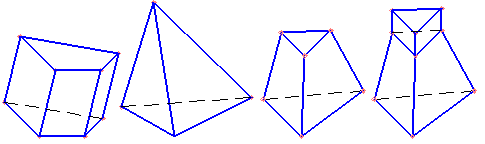
а) б) в) г)

Рисунок 3.1 - Різновиди багатогранників

Графічно багатогранники зручно задавати відповідними прямокутними проекціями його сітки (сукупності вершин та ребер). На рис. 3.2 показано утворення прямокутних проекцій піраміди, у якої грань SAD належить площині проекцій Π 1.

Рисунок 3.2 - Утворення прямокутних проекцій піраміди

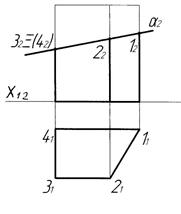
На рис. 3.3 показані прямокутні проекції піраміди, ребра та грані якої займають різне положення відносно площин проекцій.

Положення ребер:

- CD, BA – горизонтально-проекціювальне;

- CB, DA - фронтально-проекціювальне;

- SC, SD, SB, SA – загальне положення.

Положення граней:

- SBA, SCD – горизонтально-проекціювальне;

- SBC- фронтально-проекціювальне;

SDA- горизонтальне;

- BCDA - профільне.

Рисунок 3.3 - Комплексне креслення піраміди

За умови належності точки 1 грані SAB, її горизонтальна проекція 11 обов’язково знаходиться на виродженій проекції грані S1A1B1 (див. рис.3.3).

3.2 Задачі інцидентності на гранних поверхнях

До задач інцидентності відносять задачу побудови проекцій перерізів багатогранників площинами окремого положення, трактуючи її як задачу визначення проекцій сукупності точок, що одночасно належать граням багатогранника та заданій площині і являються вершинами фігури перерізу – опуклого багатокутника. На рис. 3.4 а) показана призма, зрізана фронтально-проекціювальною площиною α. Утворена фігура перерізу – чотирикутник 1234, вершинами якого є точки перетину ребер призми з площиною. Оскільки січна площина займає проекціювальне положення, то фігура перерізу має фронтальну проекцію 12223242, яка збігається з виродженою проекцією площини α 2 в межах проекції багатогранника (див. рис.3.4, б). Горизонтальна проекція перерізу 11213141 визначена за умови належності вершин чотирикутника ребрам призми, яки займають горизонтально-проекціювальне положення, тому вона збігається з горизонтальною проекцією призми.

а) б)

Рисунок 3.4 - Переріз призми

Побудова перерізу піраміди площиною β показана на рис.3.5, а. Як і у випадку побудови перерізу призми, фігурою перерізу піраміди є чотирикутник. Його вершинами є точки перетину площини з ребрами. Січна площина β займає горизонально-проекціювальне положення. Тому фігура перерізу має горизонтальну проекцію 11213141, яка збігається з виродженою проекцією площини β 1 в межах відповідної проекції піраміди (див. рис.3.5, б). Фронтальна проекція шуканого перерізу 12223242 визначена за умови належності кожної його вершини відповідному ребру піраміди.

а) б)

Рисунок 3.5 - Переріз піраміди

До задач інцидентності можна віднести і задачу побудови проекцій наскрізних отворів в гранях багатогранників, оскільки її розв’язування базується на побудові проекцій точок за умови їх належності відповідним граням (включаючи ребра) багатогранника. На рис. 3.6, а показано принцип утворення наскрізного отвору в бічних гранях піраміди. Фронтальна проекція такого отвору має вироджену проекцію у формі трикутника (див. рис. 3.6, б). Горизонтальна проекція визначена шляхом проведення допоміжних ліній в гранях піраміди, розглядаючи таким чином отвір як сукупність точок, що належать певній з граней.

а) б)

Рисунок 3.6 - Наскрізний отвір

Задачі для самостійного розв’язування