Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача №34

Побудувати три проекції наскрізних отворів

а) б)

3.3 Контрольний тест до інформаційного модуля 3

1. На якому рисунку зображені прямокутні проекції піраміди?

а) б) в)

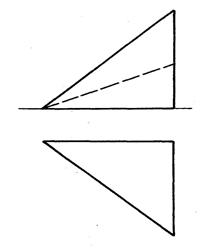
2. Скільки ребер має заданий багатогранник?

а) 6; б) 7; в) 8.

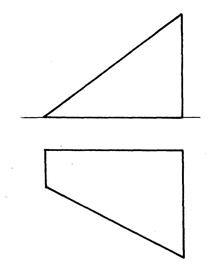
3. Скільки граней має заданий багатогранник?

а) 6; б) 7; в) 5.

4. Яка грань багатогранника займає фронтальне положення?

а) ADC; б) BEF; в) DCEF

5. На якому рисунку задана точка А, яка належить грані багатогранника?

а) б) в)

6. На якому рисунку фігура перерізу багатогранника площиною α – чотирикутник?

а) б) в) г)

ІНФОРМАЦІЙНИЙ МОДУЛЬ 4

МЕТРИЧНІ ЗАДАЧІ НА ПЕРЕТВОРЕНИХ ПРЯМОКУТНИХ ПРОЕКЦІЯХ

4.1 Метод заміни площин проекцій

Розв’язання метричних задач можна звести до чотирьох основних типів:

1) перетворення прямої загального положення в пряму рівня;

2) перетворення прямої загального положення в проекціювальну;

3) перетворення площини загального положення в проекціювальну;

перетворення площини загального положення в площину рівня.

Найбільш поширені методи, що використовуються для цього – метод заміни площин проекцій та метод плоско-паралельного переміщення. Метод заміни площин проекцій полягає в тому, що вводиться допоміжна площина проекцій, яка перпендикулярна тільки до однієї з площин проекцій (горизонтальної Π ₁, фронтальної Π ₂, профільної Π ₃) (рис. 4.1, 4.2).

Рисунок 4.1 – Система основних та додаткових площин проекцій:

Π ₄ – додаткова площина проекцій, що перпендикулярна тільки до Π ₁

Для переведення відрізка прямої із загального положення в положення рівня для визначення, наприклад, натуральної довжини, необхідно ввести додаткову площину паралельно одній з проекцій відрізка (рис. 4.3, 4.4).

a

б

Рисунок 4.2 – Утворення плоскої моделі систем площин проекцій: а – проміжний етап трансформації; б – плоска модель, що утворена в результаті трансформації

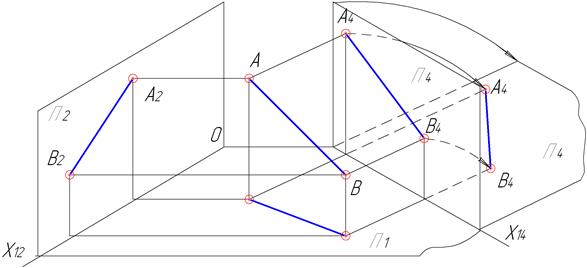
Рисунок 4.3 – Введення додаткової площини проекцій для визначення довжини відрізка загального положення

Рисунок 4.4 – Визначення довжини відрізка за умови задання АВ (А₁В₁, А₂В₂)

Для того, щоб перетворити пряму загального положення в проекціювальне положення необхідно ввести допоміжну площину перпендикулярно до проекції відрізка, яка є його натуральною величиною (рис.4.5, 4.6). Якщо пряма займає загальне положення, то переведення в проекціювальне положення відбувається в два етапи: спочатку в пряму рівня, а потім в проекціювальну пряму.

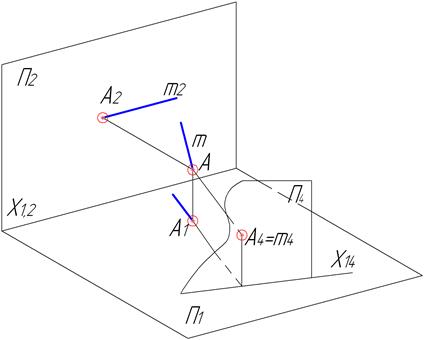
Рисунок 4.5 – Перетворення прямої рівня в проекціювальну пряму (наочне зображення)

Рисунок 4.6 – Перетворення прямої рівня в проекціювальну пряму (комплексне креслення)

Для переведення площини із загального положення в проекціювальне та в площину рівня необхідно застосувати такий алгоритм (рис.4.7):

1) вводимо горизонталь або фронталь;

2) вводимо допоміжну площину проекцій перпендикулярно до горизонтальної проекції горизонталі;

3) переводимо площину в проекціювальне положення;

4) вводимо нову допоміжну площину паралельно площині в проекціювальному положенні;

5) переводимо площину в натуральну величину.

Розглянемо геометричні підстави для розв’язання деяких метричних задач.

Рисунок 4.7 – Перетворення проекціювальної площини в площину рівня

Для визначення відстані між двома паралельними прямими необхідно перевести обидві прямі в проекціювальне положення (рис. 4.8). Якщо прямі займають загальне положення, то необхідно провести два послідовних перетворення: спочатку ввести додаткову площину для переведення прямих в натуральну величину, а потім ввести додаткову площину перпендикулярно до отриманих проекцій прямих.

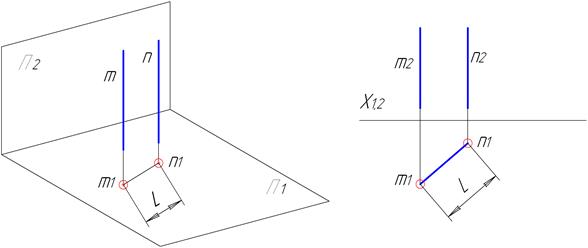
Рисунок 4.8 – Визначення відстані між двома паралельними прямими

Рисунок 4.9 – Визначення відстані між двома мимобіжними прямими

Для визначення відстані між двома мимобіжними прямими необхідно знайти найкоротшу відстань. Для цього необхідно виконати перетворення таким чином, щоб одна з прямих зайняла проекціювальне положення, тобто спроекціювалася в точку. Перпендикуляр з цієї точки визначає шукану відстань (рис.4.9). Якщо обидві прямі початково займають загальне положення, то перетворення відбувається в два етапи: 1) вводиться додаткова площина проекцій таким чином, щоб одна з прямих спроекціювалась в натуральну величину; 2) вводиться додаткова площина перпендикулярно до отриманої натуральної величини.

Для визначення відстані між точкою та площиною необхідно перетворити площину в проекціювальне положення та опустити перпендикуляр з отриманої проекції точки на пряму, що є проекцією площини (рис.4.10). Якщо площина займає загальне положення, то потрібно спочатку перевести задану площину в проекціювальне положення (рис.4.7).

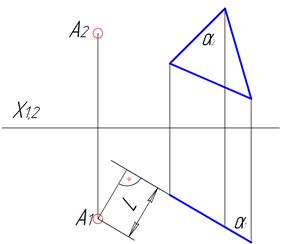
Рисунок 4.10 – Визначення відстані між точкою та площиною

Для визначення величини двогранного кута між площинами необхідно ввести додаткову площину перпендикулярно до ребра, при якому визначається кут, тобто перевести вказане ребро в проекціювальне положення. При цьому кожна площина спроекціюється в пряму (рис.4.11). Якщо ребро при двогранному куті займає загальне положення, то потрібно спочатку перевести його в натуральну величину, а вже потім – в точку.

Рисунок 4.11 – Визначення величини двогранного кута між площинами

Задачі для самостійного розв’язування