
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 92
|
|
В однородном магнитном поле, индукция которого В =0, 1 Тл, вращается катушка, состоящая из N =200 витков. Ось вращения катушки перпендикулярна и ее оси и к направлению магнитного поля. Период обращения катушки Т =0, 2 с, площадь поперечного сечения S =4 см2. Найти максимальную э.д.с. индукции Еmax во вращающейся катушке.
| Дано: В =0, 1 Тл N =200 S = 10-4 м2 t =0, 2c | Решение: Рассмотрим один виток соленоида. Магнитный поток, пронизывающий этот виток, изменяется по гармоническому закону Ф = BS cos j |
| Еmax -? | Как мы знаем, э.д.с. индукции в витке |


|
Угол j меняется со временем как j = wt,
где w - циклическая частота, равная
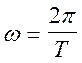
Отсюда


|
где Eo=BSw - максимальное значение э.д.с. индукции в витке.
Так как катушка представляет собой совокупность витков, то
Emax = NE0
или

Вычисления:

Ответ: максимальная э.д.с. индукции во вращающейся катушке равна  .
.
|
|
