Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Задача 83

Электрон, ускоренный разностью потенциалов U =l кВ влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Индукция магнитного поля В =1, 19 мТл. Найти радиус R окружности, по которой движется электрон, период обращения Т и момент импульса М электрона.

Дано: U =l000В В =1, 19·10-3 Тл т0 = 9, 1·10-31 кг	Решение: Если ускоряющее поле совершает над частицей массой m и зарядом е работу A=eU, то частица приобретает кинетическую энергию
R, T, M -?	Согласно закону сохранения и превращения

энергии

(1)

Сила Лоренца сообщает заряду перпендикулярное к скорости ускорение

(т.к. угол между u и В прямой).

Это ускорение изменяет лишь направление скорости, величина же скорости остается неизменной. Следовательно, и ускорение будет постоянным по величине. При этих условиях заряженная частица движется равномерно по окружности, радиус которой определяется соотношением

Подставив сюда значение для и решив получившееся уравнение относительно R, получим

(2)

Подставив (1)в (2), получаем:

Найдем время Т, затрачиваемое на один оборот.

Для этого разделим длину окружности 2p R на скорость u:

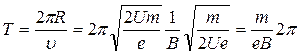
Момент импульса электрона определяется формулой

M = m u R.

Подставим ранее полученные формулы, получаем

Вычисления:

Ответ: радиус окружности, по которой движется частица равен R =9 см, период обращения электрона по этой окружности равен Т =30 нс, момент импульса электрона